-
1、已知双曲线 .(1)、若直线l与双曲线C相交于A,B两点,线段AB的中点坐标为 , 求直线l的方程;(2)、若P为双曲线C右支上异于右顶点的一个动点,F为双曲线C的右焦点,x轴上是否存在定点 , 使得?若存在,求出t的值;若不存在,请说明理由.
-
2、如图,在三棱柱中,底面是边长为4的等边三角形,且 .
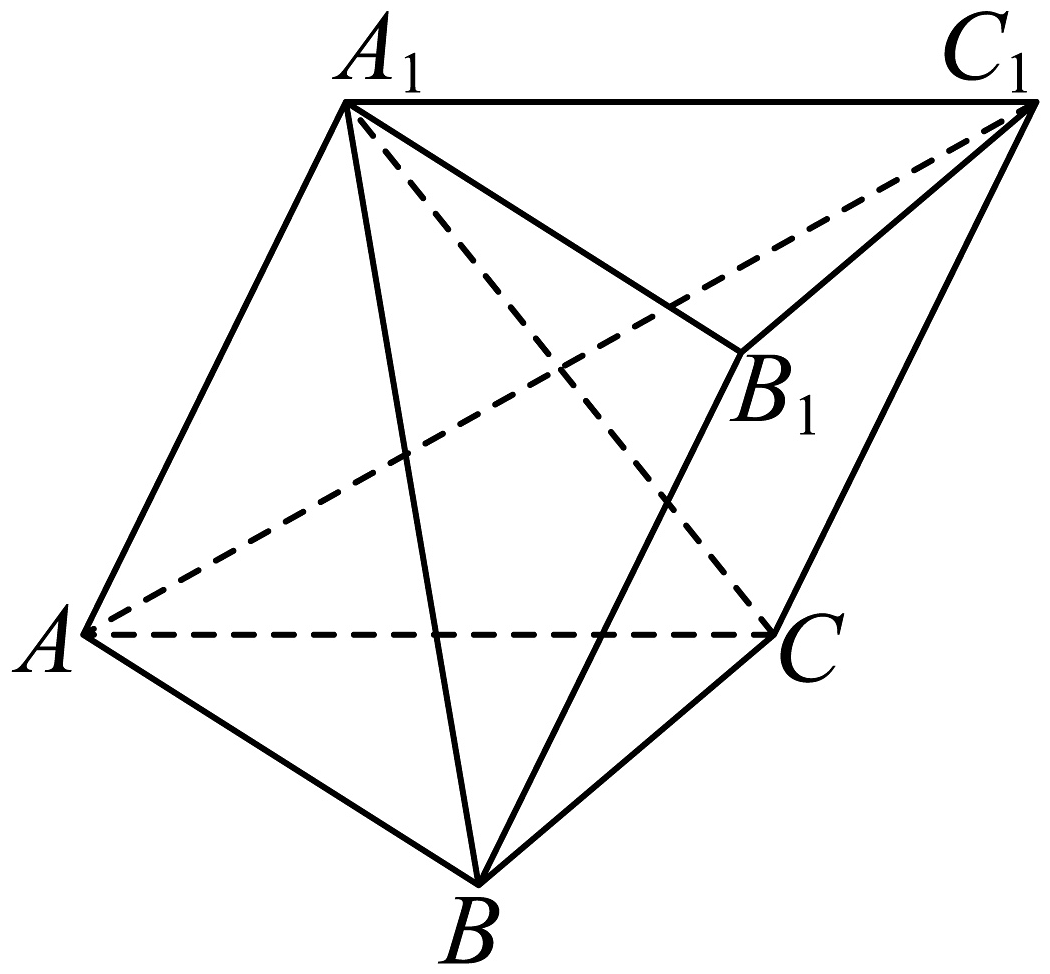 (1)、求证:;(2)、若三棱柱的体积为 , 求直线与平面所成角的正弦值.
(1)、求证:;(2)、若三棱柱的体积为 , 求直线与平面所成角的正弦值. -
3、为减少环境污染,保护生态环境,某校进行了“垃圾分类知识普及活动”,并对高一、高二全体学生进行了相关知识测试.现从高一、高二各随机抽取了20名学生,对他们的成绩(百分制)进行了整理和分析后得到如下信息:
高一年级成绩分布表
成绩
人数
1
2
3
4
10
高二年级成绩频率分布直方图
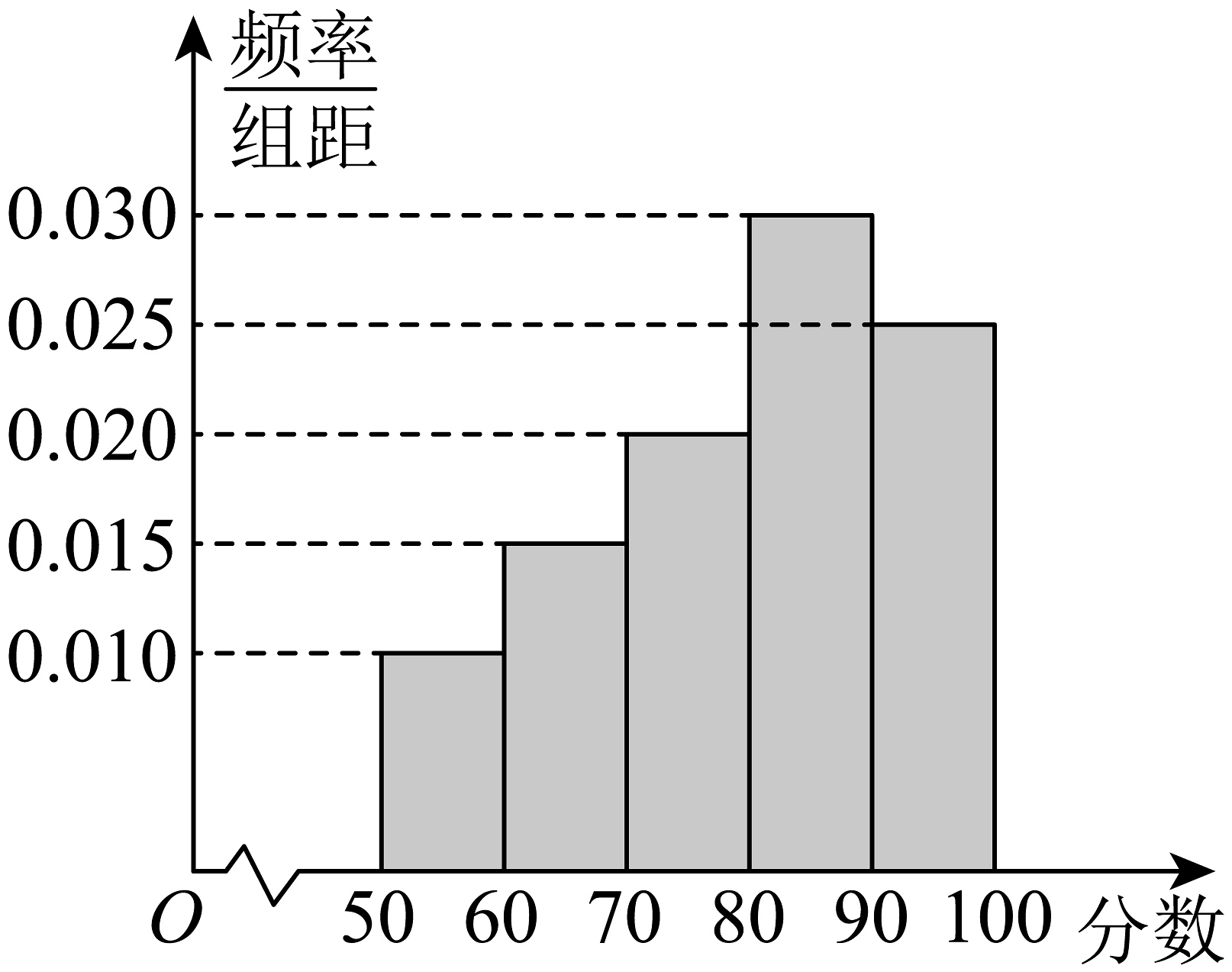 (1)、从高一和高二样本中各抽取一人,求这两人成绩都不低于90分的概率;(2)、用频率估计概率,分别从高一全体学生中抽取一人,从高二全体学生中抽取两人,随机变量表示这三人中成绩不低于90分的人数,求的分布列和数学期望.
(1)、从高一和高二样本中各抽取一人,求这两人成绩都不低于90分的概率;(2)、用频率估计概率,分别从高一全体学生中抽取一人,从高二全体学生中抽取两人,随机变量表示这三人中成绩不低于90分的人数,求的分布列和数学期望. -
4、已知棱长为1的正方体 , 在其内部放入两个相外切的球和球(可与正方体表面相切),半径分别为 , 则的最大值为 .
-
5、在中,角A,B,C的对边分别为a,b,c,若 , 则的面积为 .
-
6、椭圆的焦点为、 , 以为圆心作一个圆,使此圆过椭圆中心并交椭圆于、两点,若直线与圆相切,则 .
-
7、函数的图象被称为牛顿三叉戟曲线,以下图象可能为函数的图象的是( )A、
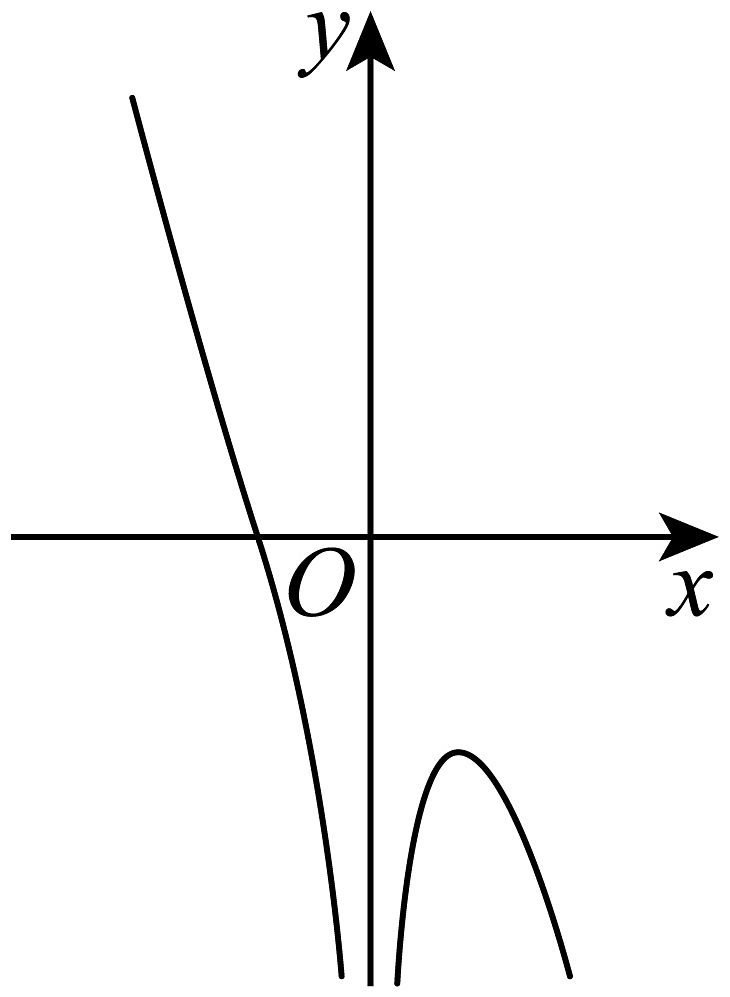 B、
B、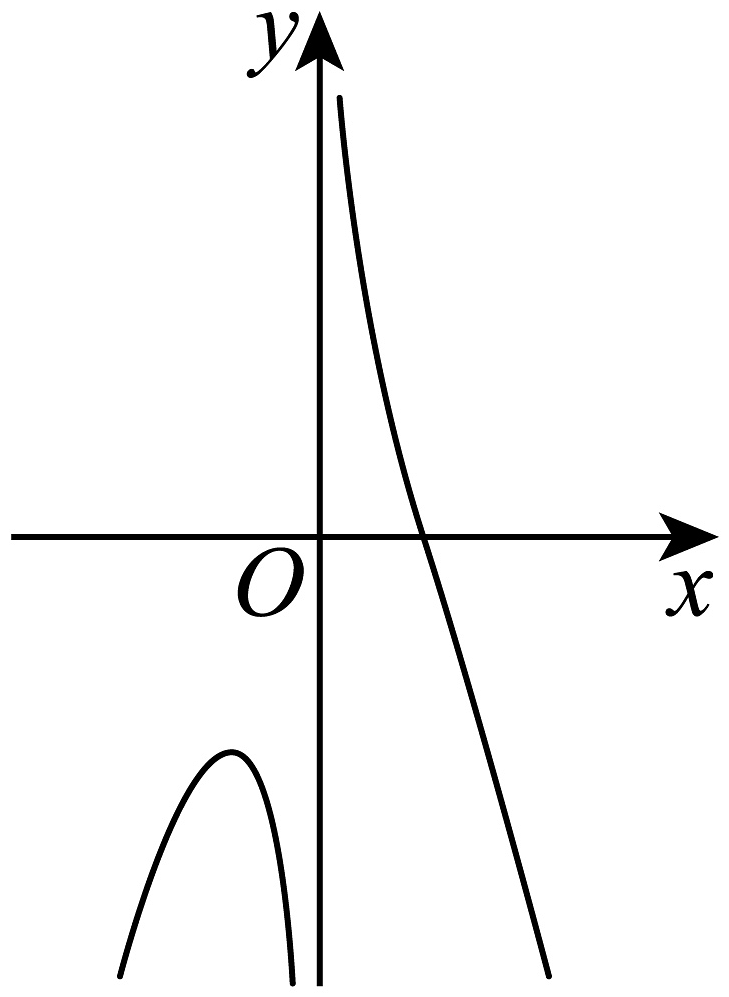 C、
C、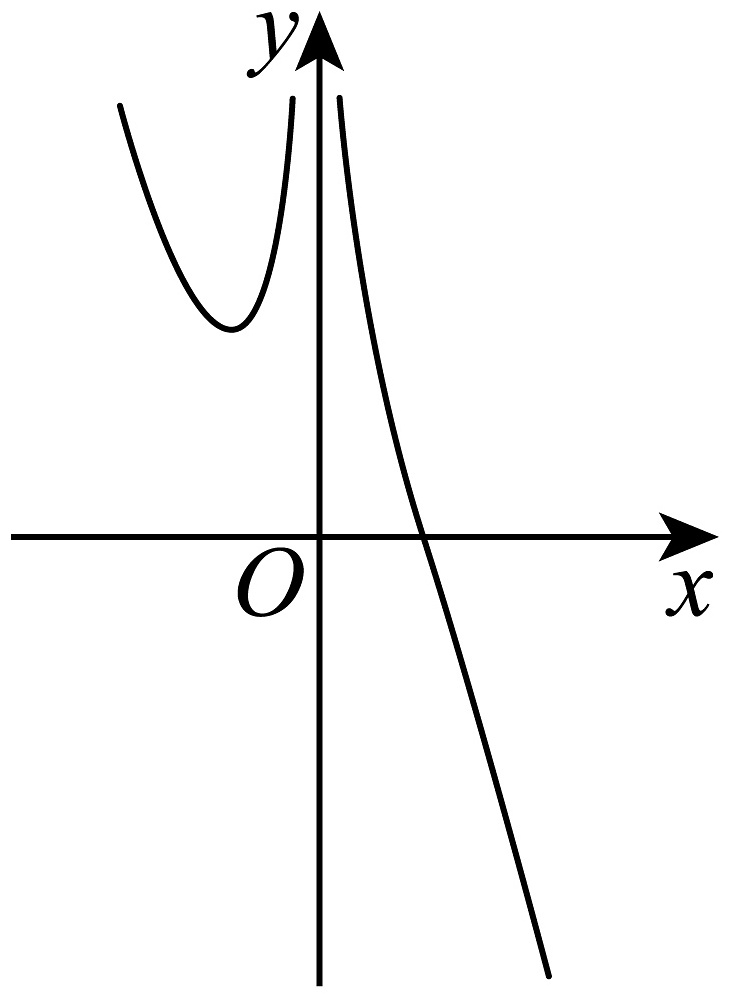 D、
D、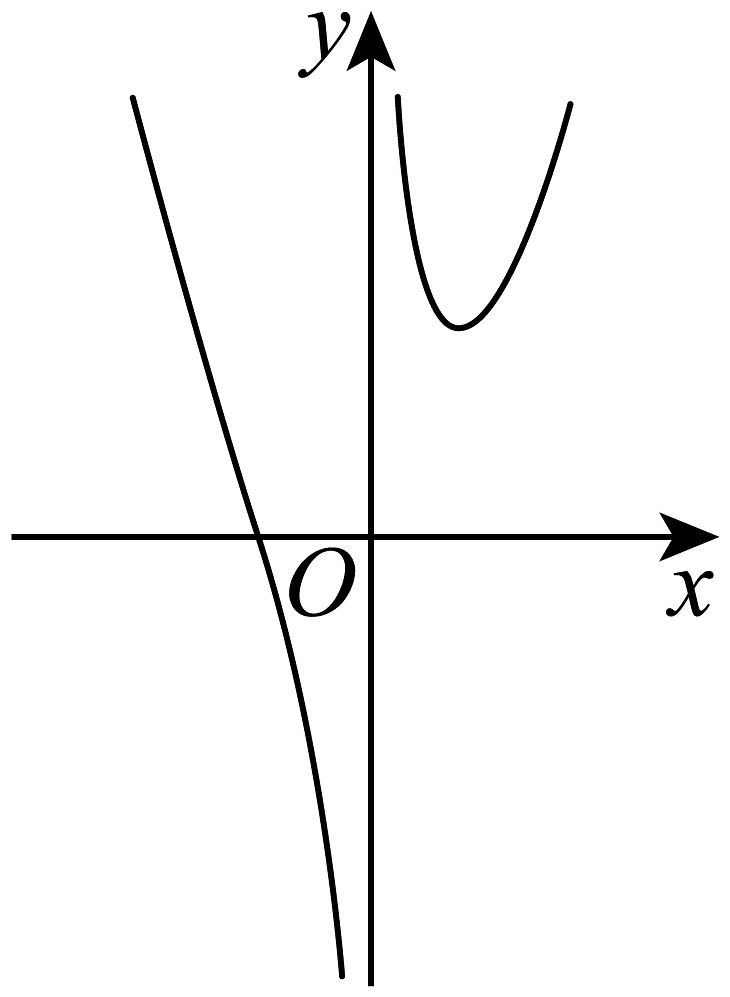
-
8、某次测验中,高三(1)班m位同学参加考试,平均分为 , 方差为 , 高三(2)班n位同学参加考试,平均分为 , 方差为 , 两个班总的平均分为 , 方差为 , 则下列说法一定正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
9、在的展开式中,下列说法正确的是( )A、展开式共项 B、各项系数的和为1 C、项的系数为 D、二项式系数最大的项为第项
-
10、一个质地均匀的正八面体的八个面上分别标有数字1到8,将其随机抛掷两次,记与地面接触面上的数字依次为 , 事件A: , 事件B: , 事件C: , 则( )A、A,B互斥 B、 C、 D、A,B,C两两独立
-
11、已知函数的部分图象如图所示,若A,B,C是直线与函数图象的从左至右相邻的三个交点,且 , 则( )
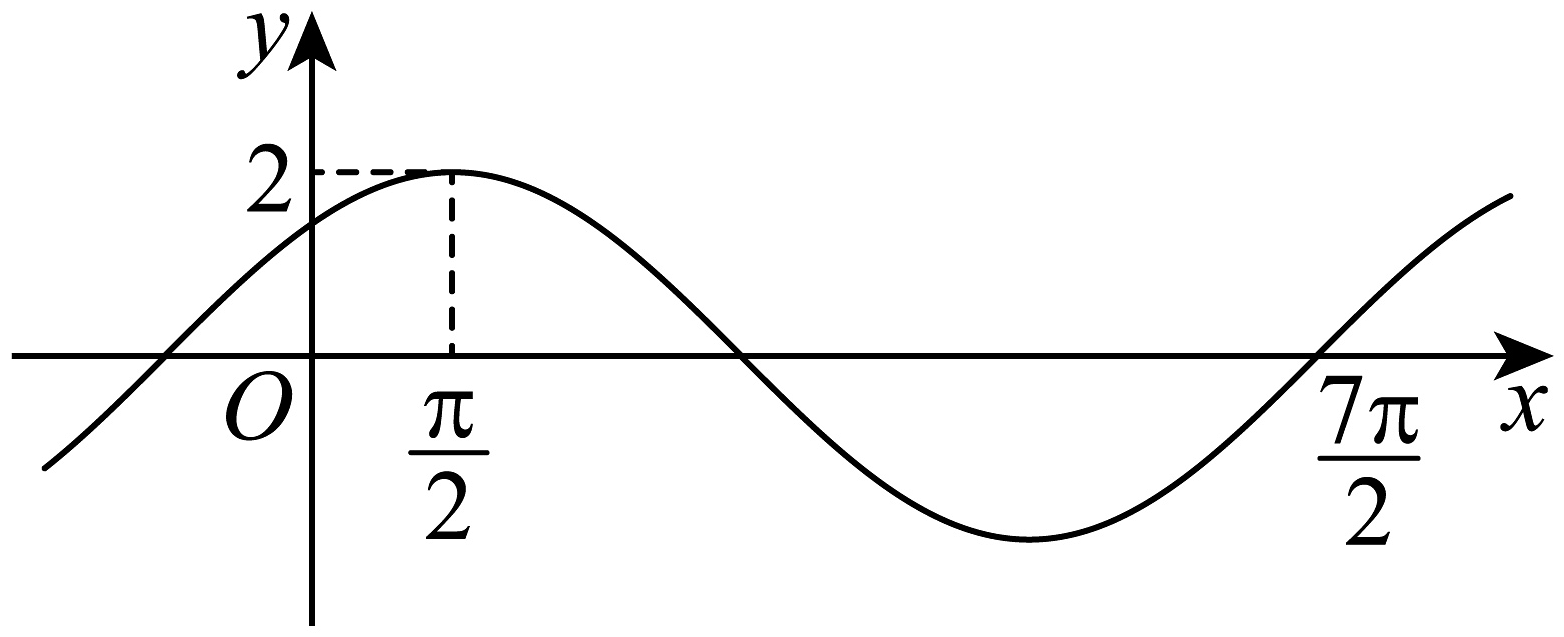 A、1 B、 C、 D、
A、1 B、 C、 D、 -
12、已知抛物线的焦点为 , 点为上的不同两点,若线段的中点到轴的距离为2,则的最大值为( )A、3 B、6 C、9 D、36
-
13、已知奇函数和偶函数的定义域均为 , 且满足 , 则( )A、1 B、 C、 D、
-
14、设是方程的两根,则( )A、p B、 C、 D、
-
15、某校新建一个报告厅,要求容纳840个座位,报告厅共有21排座位,从第2排起后一排都比前一排多2个座位,则第1排应安排的座位数为( )A、18 B、19 C、20 D、21
-
16、已知 , 则( )A、 B、 C、0 D、
-
17、已知向量不共线,与共线,则实数的值为( )A、 B、2 C、6 D、
-
18、已知随机变量 , , , 则的最小值为( )A、 B、 C、 D、
-
19、若 , 则( )A、 B、 C、 D、
-
20、若函数的定义域为 , 都有 , 则称函数为中心对称函数,其中为函数的对称中心.(1)、已知定义R上的函数的图象关于点中心对称,且当时, , 求 , 的值;(2)、探究函数是否为中心对称函数.若是,请求出对称中心并用定义证明;若否,请说明理由.(3)、运用第(2)问的结论,求的值,其中 .