-
1、设m,n为直线,α,β为平面,则下列结论正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
2、如图1,在等腰梯形中, , 将沿折起,使得点落在点的位置,得到三棱锥 , 如图2所示.则当二面角的平面角的大小为时,三棱锥的外接球的表面积为( )
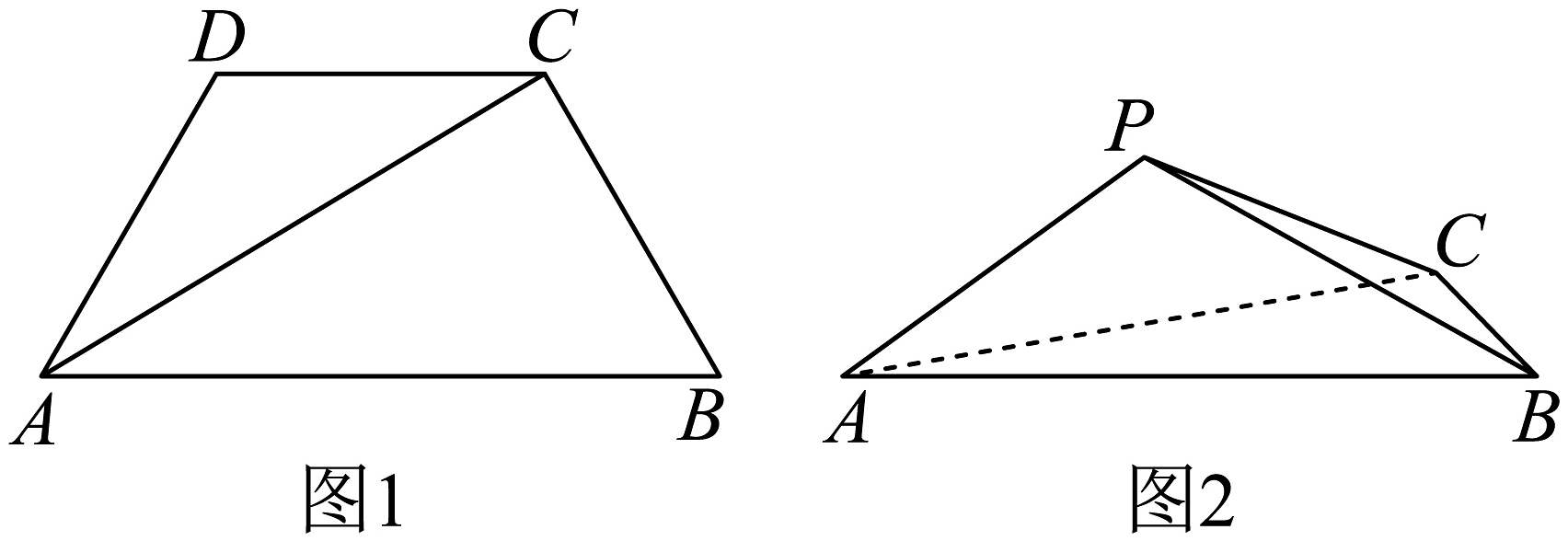 A、 B、 C、 D、
A、 B、 C、 D、 -
3、如图,某实心零部件的形状是正四棱台,已知 , , 棱台的高为 , 现需要对该零部件的表面进行防腐处理,若每平方厘米的防腐处理费用为0.5元,则该零部件的防腐处理费用是( )
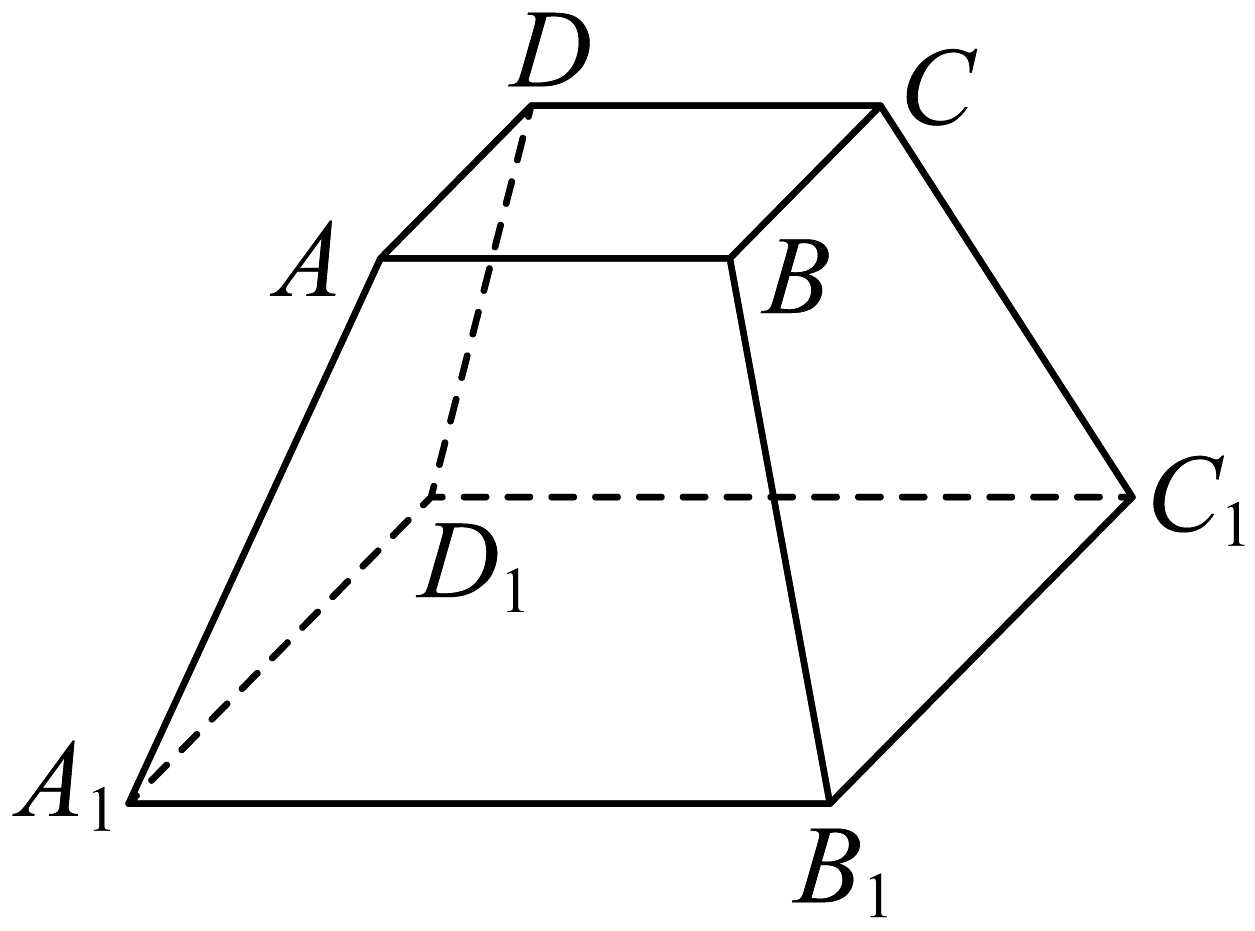 A、160元 B、128元 C、97.5元 D、86.875元
A、160元 B、128元 C、97.5元 D、86.875元 -
4、某校组织50名学生参加庆祝中华人民共和国成立75周年知识竞赛,经统计这50名学生的成绩都在区间内,按分数分成5组: , , , , , 得到如图所示的频率分布直方图(不完整),根据图中数据,下列结论正确的是( )
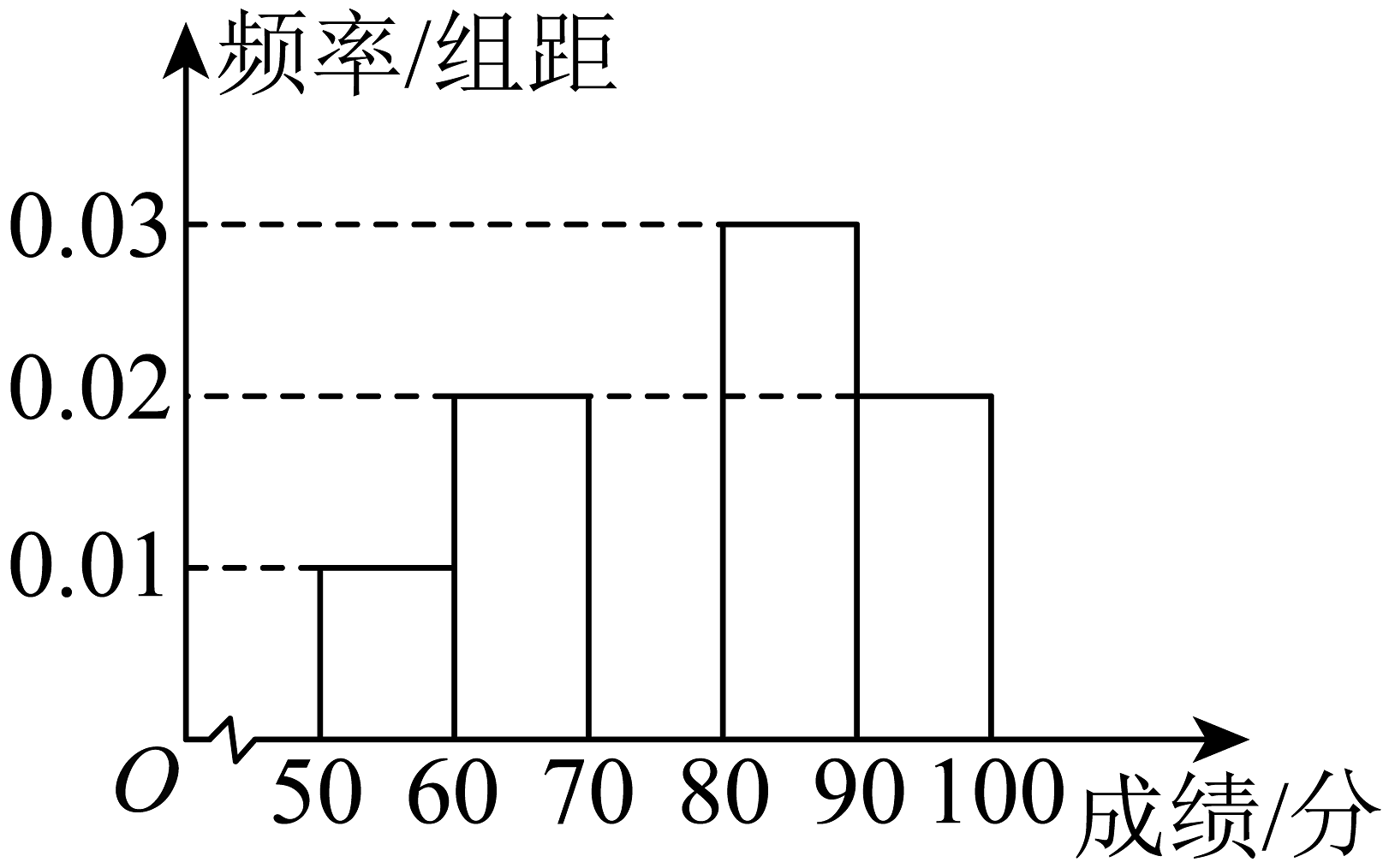 A、成绩在上的人数最多 B、成绩不低于70分的学生所占比例为70% C、50名学生成绩的平均分小于中位数 D、50名学生成绩的极差为50
A、成绩在上的人数最多 B、成绩不低于70分的学生所占比例为70% C、50名学生成绩的平均分小于中位数 D、50名学生成绩的极差为50 -
5、在中,角 , , 的对边分别为 , , , 面积为S.若 , , 且 , 则( )A、 B、 C、 D、
-
6、( )A、 B、 C、 D、
-
7、已知平面向量 , , 则向量在向量上的投影向量的坐标为( )A、 B、 C、 D、
-
8、已知向量 , , 若 , 则k的值为( )A、 B、 C、-3 D、3
-
9、已知 , 则( )A、 B、 C、 D、1
-
10、已知函数是偶函数.(1)、求实数的值;(2)、若关于的方程有且仅有一个实数根,求实数的取值范围.
-
11、某企业生产某批产品按产品质量(单位:g)从高到低依比例划定A,B,C,D,E五个等级,A等级优于B等级,B等级优于C等级,C等级优于D等级,D等级优于E等级.其中A等级产品占该批产品的12%,B等级产品占该批产品的32%,C等级产品占该批产品的37%,D等级产品占该批产品的15%,E等级产品占该批产品的4%.现从该批产品中随机抽取100件产品对其质量进行分析,并绘制出如图所示的频率分布直方图,其中 .
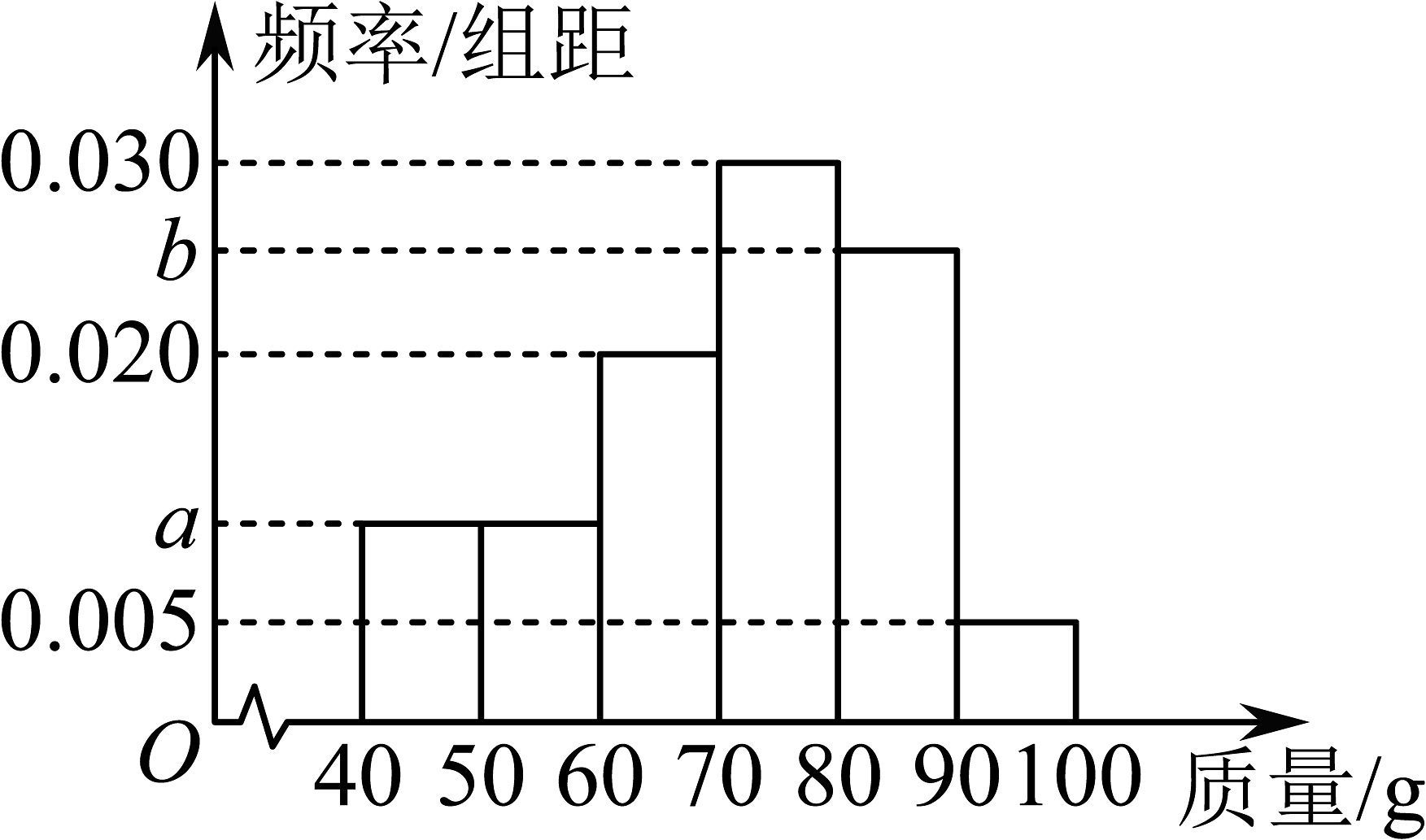 (1)、求图中a,b的值;(2)、根据频率分布直方图,估计企业生产的该批产品的质量的平均数(同一组的值用该组区间的中点值作为代表);(3)、用样本估计总体的方法,估计该批产品中C等级及以上等级的产品质量至少为多少g?
(1)、求图中a,b的值;(2)、根据频率分布直方图,估计企业生产的该批产品的质量的平均数(同一组的值用该组区间的中点值作为代表);(3)、用样本估计总体的方法,估计该批产品中C等级及以上等级的产品质量至少为多少g? -
12、(多选)已知函数 , 则以下结论正确的是( )A、函数的单调减区间是 B、函数有且只有1个零点 C、存在正实数 , 使得成立 D、对任意两个正实数 , , 且 , 若则
-
13、已知数列的前n项和为 , 前n项积为 , , 且 . ( )A、若数列为等差数列,则 B、若数列为等差数列,则 C、若数列为等比数列,则 D、若数列为等比数列,则
-
14、分别抛掷两枚质地均匀的硬币,设事件“第一枚正面朝上”,事件“第二枚正面朝上”,则下列结论正确的是( )A、 B、 C、事件与互斥 D、事件与相互独立
-
15、若 , 则( )A、 B、 C、 D、
-
16、已知椭圆的短轴长为2,离心率为 .(1)、求的方程;(2)、若 , 分别是的左、右顶点,不与轴垂直的动直线与交于 , 两点(不同于 , ),且直线的斜率等于直线的斜率的2倍,求证:直线经过定点.
-
17、已知函数.
(1)求函数的最小正周期;
(2)求函数的单调递增区间;
(3)求函数在区间上的值域.
-
18、随机变量 , 若 , 则实数的值为( )A、2 B、 C、3 D、4
-
19、以下数据为参加某次数学竞赛的15人的成绩(单位:分),分数从低到高依次是:56、70、72、78、79、80、81、83、84、85、88、90、91、94、98,则这15人成绩的第60百分位数是 .
-
20、已知向量 , , 若 , 则实数的值为( )A、 B、 C、4 D、12