版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知集合 $A = \{x |x \geq 3\}$ ， $B = \{x |1 \leq x \leq 7\}$ ， $C = \{x |x \geq a - 1\}$ .

(1)、求 $A \cap B$ ， $∁_{R} (A \cup B)$ ， $(∁_{R} A) \cap B$ ；

(2)、若 $C \cup A = C$ ，求实数 $a$ 的取值范围.

查看解析
2、已知函数 $f (x) = \{\begin{array}{l} \begin{array}{l} (3 a - 1) x + 4 a, x < 1 \\ \frac{a}{x}, x \geq 1 \end{array} \end{array}$ ，满足对任意的实数 $x_{1}, x_{2}$ 且 $x_{1} \neq x_{2}$ ，都有 $[f (x_{1}) - f (x_{2})] (x_{1} - x_{2}) < 0$ ，则实数a的取值范围是.

查看解析
3、函数 $f (x) = |x - 2| x$ 的单调递增区间为．

查看解析
4、高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设 $x \in R$ ，用 $[x]$ 表示不超过x的最大整数，则 $y = [x]$ 称为高斯函数，如 $[3.24] = 3, [- 1.5] = - 2$ .设函数 $f (x) = x - [x]$ ，则下列说法错误的是（）

A、 $f (x)$ 的图象关于 $y$ 轴对称 B、 $f (x)$ 的最大值为1，没有最小值 C、 $f (\sqrt{6}) + f (\sqrt{13}) > 1$ D、 $f (x)$ 在 $R$ 上是增函数

查看解析
5、下列四个结论中，正确的结论是（）

A、 $y = \sqrt{1 + x} \cdot \sqrt{1 - x}$ 与 $y = \sqrt{1 - x^{2}}$ 表示同一个函数． B、“ $1 < x < 3$ ”的充分不必要条件是“ $0 \leq x \leq 4$ ”． C、已知 $2 < a < 3, - 2 < b < - 1$ ，则 $\frac{a}{b}$ 的取值范围的取值范围是 $(- 3, - 1)$ ． D、函数 $y = x + \sqrt{x - 1}$ 的值域为 $[\frac{3}{4}, + \infty)$ ．

查看解析
6、给出下列四个命题，其中正确命题的是（）

A、若 $a > b, c > d$ ，则 $a c > b d$ ； B、若 $a^{2} x > a^{2} y$ ，则 $x > y$ ； C、若 $a > b$ ，则 $\frac{1}{a - b} > \frac{1}{a}$ ； D、若 $\frac{1}{a} < \frac{1}{b} < 0$ ，则 $a b < b^{2}$ .

查看解析
7、已知 $f (x)$ 是定义在 $(- \infty ， 0) \cup (0 ， + \infty)$ 上的偶函数，对任意的 $x_{1}, x_{2} \in (0 ， + \infty)$ 满足 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} > 0$ 且 $f （ 2 ） = 4$ ，则不等式 $f (x) \geq 4$ 的解集为（）

A、 $[- 2 ， 0) \cup [2, + \infty)$ B、 $[- 2 ， 0) \cup (0 ， 2]$ C、 $(- \infty ， - 2]\cup[2 ， + \infty)$ D、 $(- \infty, - 2] \cup (0, 2]$

查看解析
8、若命题“对任意 $x \in (- \infty, 0)$ ，使得 $x^{2} - 2 a x + 4 \geq 0$ 成立”是真命题，则实数a的取值范围是（）

A、 $[- 2, + \infty)$ B、 $[2, + \infty)$ C、 $(- \infty, - 2]$ D、 $(- \infty, 2]$

查看解析
9、已知函数 $f (x) = \{\begin{array}{l} f (x - 2), x \geq 0 \\ 2 x^{2} - 3 x, x < 0 \end{array}$ ，则 $f (f (1)) =$ （）

A、 $14$ B、 $5$ C、1 D、 $- 1$

查看解析
10、函数 $y = \frac{\sqrt{4 - |x|}}{x}$ 的定义域是（）

A、 $[- 2, 2]$ B、 $(- 2, 2)$ C、 $[- 2, 0) \cup (0, 2]$ D、 $[- 4, 0) \cup (0, 4]$

查看解析
11、已知集合 $A = \{x |- 1 < x < 5\}$ ， $B = \{x |x \geq 0\}$ ，则图中阴影部分表示的集合为

A、 $\{x |- 1 < x < 0\}$ B、 $\{x |0 < x < 5\}$ C、 $\{x |0 \leq x < 5\}$ D、 $\{x |x > - 1\}$

查看解析
12、为鼓励青年大学生积极参与暑期社会实践，某高校今年暑假组织返乡大学生积极参与了当地的暑假社区儿童托管服务.现抽样调查了其中100名大学生，统计他们参加社区托管活动的时间（单位：小时），并将统计数据制成如图所示的频率分布直方图.另外，根据参加社区托管活动的时间从长到短按3：4：3的比例分别被评为优秀､良好､合格.

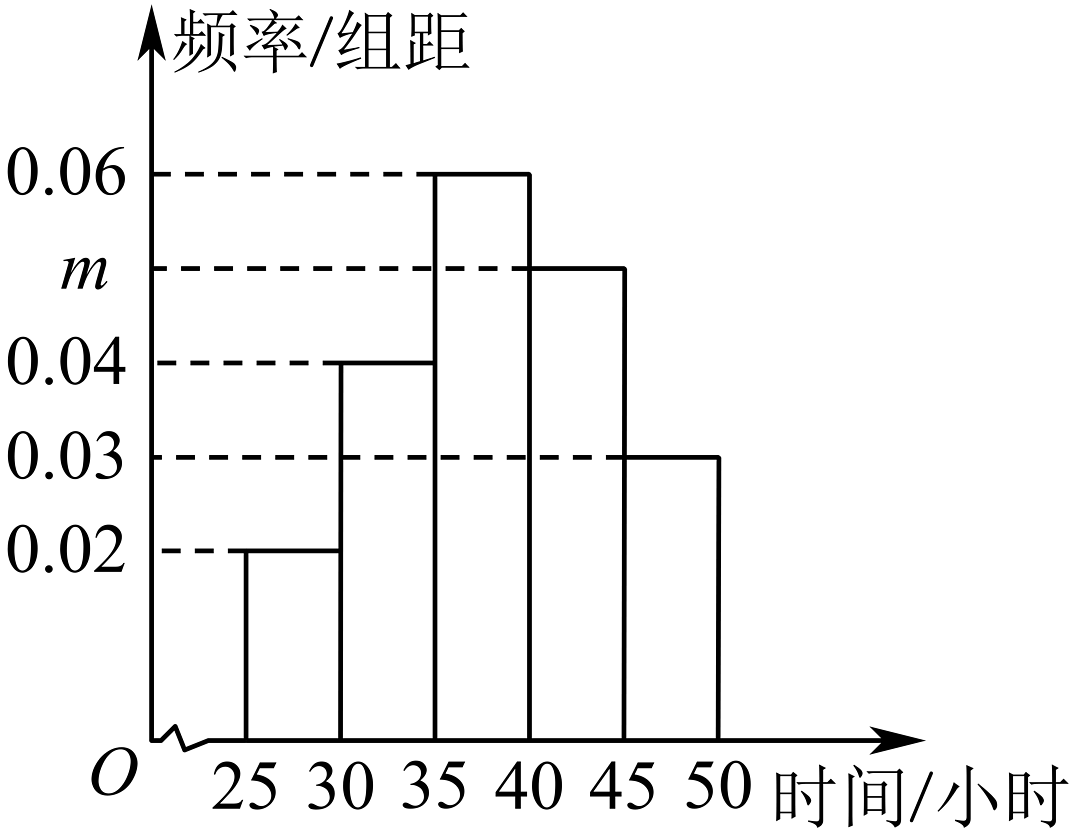(1)、求 $m$ 的值，并估计该校学生在暑假中参加社区托管活动的时间的平均数（同一组中的数据用该组区间的中点值作代表）；

(2)、试估计至少参加多少小时的社区托管活动，方可以被评为优秀.

查看解析
13、已知一组数据： $3, 5, 7, x, 9$ 的平均数为6，则该组数据的 $40 %$ 分位数为（）

A、4.5 B、5 C、5.5 D、6

查看解析
14、函数 $f (x) = \{\begin{array}{l} \frac{x + 1}{x}, x < 0 \\ \frac{3 x}{e^{x}}, x \geq 0 \end{array}$ ，关于x的方程 $f^{2} (x) - m |f (x)| = 0 (m \in R)$ ，则下列正确的是（）

A、函数 $f (x)$ 的值域为R B、函数 $f (x)$ 的单调减区间为 $(- \infty, 0), [1, + \infty)$ C、当 $m = \frac{1}{2}$ 时，则方程有4个不相等的实数根 D、若方程有3个不相等的实数根，则m的取值范围是 $(\frac{3}{e}, + \infty)$

查看解析
15、已知平面向量 $\vec{m}, \vec{n}$ 满足： $|\vec{m}| = |\vec{n}| = 2$ ，且 $\vec{m}$ 在 $\vec{n}$ 上的投影向量为 $\frac{1}{2} \vec{n}$ ，则向量 $\vec{m}$ 与向量 $\vec{n} - \vec{m}$ 的夹角为（）

A、 $30 °$ B、 $60 °$ C、 $120 °$ D、 $150 °$

查看解析
16、已知数列 $\{a_{n}\}$ 满足 $a_{n + 1} = \frac{2}{3} a_{n} + 4$ ，且 $a_{1} = 1$ ，则 $\{a_{n}\}$ 的通项公式为（）

A、 $a_{n} = 12 - {(\frac{2}{3})}^{n - 1}$ B、 $a_{n} = {(\frac{2}{3})}^{n + 2}$ C、 $a_{n} = 12 - 11 \times {(\frac{2}{3})}^{n - 1}$ D、 $a_{n} = 8 + {(\frac{2}{3})}^{n - 1}$

查看解析
17、已知 $|\vec{a}| = 1$ ， $|\vec{b}| = \sqrt{2}$ ， $⟨\vec{a}, \vec{b}⟩ = \frac{π}{4}$ ．

(1)、求 $|\vec{a} + \vec{b}|$ ；

(2)、若 $(k \vec{a} + \vec{b}) ⊥ (\vec{a} - 2 \vec{b})$ ，求实数k的值．

查看解析
18、若椭圆焦点在 $x$ 轴上且经过点 $(- 4, 0)$ ，焦距为6，则该椭圆的标准方程为（）

A、 $\frac{x^{2}}{16} + \frac{y^{2}}{8} = 1$ B、 $\frac{x^{2}}{16} + \frac{y^{2}}{7} = 1$ C、 $\frac{x^{2}}{9} + \frac{y^{2}}{16} = 1$ D、 $\frac{x^{2}}{7} + \frac{y^{2}}{16} = 1$

查看解析
19、对于四个正数m、n、p、q，若满足 $m q < n p$ ，则称有序数对 $(m, n)$ 是 $(p, q)$ 的“下位序列”．

(1)、对于2、3、7、11，有序数对 $(3, 11)$ 是 $(2, 7)$ 的“下位序列”吗？请简单说明理由；

(2)、设a、b、c、d均为正数，且 $(a, b)$ 是 $(c, d)$ 的“下位序列”，试判断 $\frac{a}{b}$ 、 $\frac{c}{d}$ 、 $\frac{a + c}{b + d}$ 之间的大小关系；

(3)、设正整数n满足条件：对集合 $\{m |0 < m < 2024, m \in N\}$ 内的每个m，总存在正整数k，使得 $(m, 2024)$ 是 $(k, n)$ 的“下位序列”，且 $(k, n)$ 是 $(m + 1, 2025)$ 的“下位序列”，求正整数n的最小值．

查看解析
20、如图，在三棱锥 $P - A B C$ 中， $A_{1}$ ， $B_{1}$ ， $C_{1}$ 分别是侧棱 $P A$ ， $P B$ ， $P C$ 的中点， $A B ⊥ B C$ ， $A_{1} C ⊥$ 平面 $B B_{1} C_{1} C$ .

(1)、求证：平面 $A_{1} B_{1} C ⊥$ 平面 $A_{1} B_{1} C_{1}$ ；

(2)、如果 $A_{1} C = B_{1} C$ ， $A B = B C = 4$ ，求二面角 $A_{1} - B B_{1} - C$ 的余弦值.

查看解析

上一页 980 981 982 983 984 下一页跳转