相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、记为等差数列的前n项和,公差为d,若 , 则以下结论一定正确的是( )A、 B、 C、 D、取得最大值时,
-
2、以圆:与圆:相交的公共弦为直径的圆的方程为( )A、 B、 C、 D、
-
3、已知A为抛物线上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p=( )A、4 B、6 C、8 D、10
-
4、虚轴长为2,离心率的双曲线两焦点为 , , 过作直线交双曲线的一支于、两点,且 , 则的周长为( )A、3 B、16+ C、12+ D、24
-
5、已知点 , , 直线的斜率为 , 直线的斜率为 , 若 , 则点的轨迹为不包含 , 两点的( )A、直线 B、椭圆 C、双曲线 D、抛物线
-
6、若直线与圆相交于 , 两点,且(为坐标原点),则( )A、1 B、 C、2 D、
-
7、直线的倾斜角及在y轴上的截距分别是( )A、 , 2 B、 , C、 , D、 , 2
-
8、已知椭圆的左焦点为 , 离心率为 , 为上一点,为圆上一点,的最大值为 .(1)、求椭圆的标准方程;(2)、若圆与轴正半轴交于点 , 过作直线 , 与相交于不同的两点 , , 求面积的最大值.
-
9、已知在中,角的对边分别为 , 且 .(1)、求角;(2)、若为边上一点,且 , 求的值.
-
10、三棱锥中, , 平面平面 , 且.记的体积为 , 内切球半径为 , 则的最小值为.
-
11、已知等差数列的前项和为 , 公差为 , 若也为等差数列,则的值为( )A、2 B、3 C、4 D、8
-
12、如图所示,棱长为3的正方体中,P为线段上的动点(不含端点),则下列结论正确的是( )
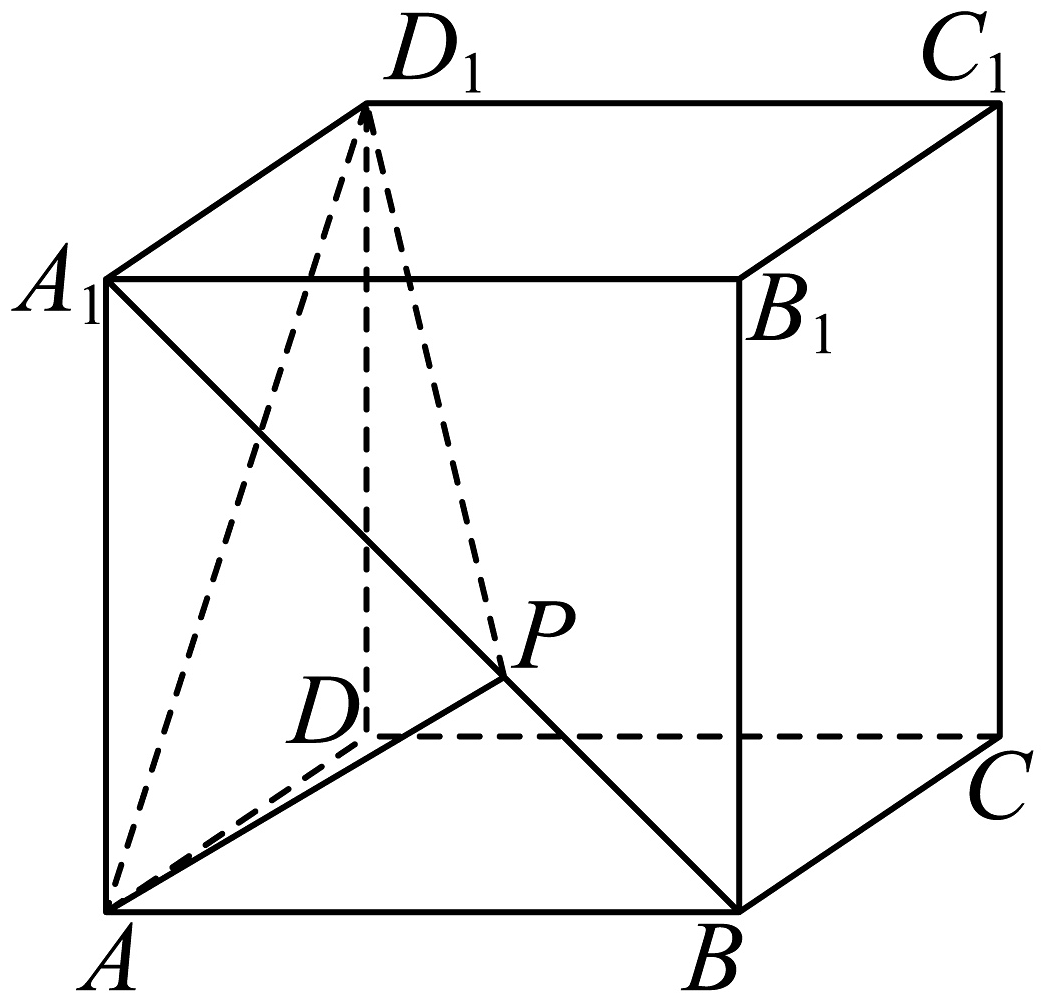 A、 B、与所成的角可能是 C、是定值 D、当时,点到平面的距离为2
A、 B、与所成的角可能是 C、是定值 D、当时,点到平面的距离为2 -
13、已知空间中三个向量 , , , 则下列说法正确的是( )A、与是共线向量 B、与同向的单位向量是 C、在方向上的投影向量是 D、与的夹角为
-
14、若函数至少有一个零点,则的取值范围为( )A、 B、 C、 D、
-
15、意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列称为“斐波那契数列”.记斐波那契数列为 , 其前项和为 , 则( )A、 B、 C、 D、
-
16、过曲线上一点作其切线,若恰有两条,则称为的“类点”;过曲线外一点作其切线,若恰有三条,则称为的“类点”;若点为的“类点”或“类点”,且过存在两条相互垂直的切线,则称为的“类点”.(1)、设 , 判断点是否为的“类点”,并说明理由;(2)、设 , 若点为的“类点”,且过点的三条切线的切点横坐标可构成等差数列,求实数的值;(3)、设 , 证明:轴上不存在的“类点”.
-
17、已知椭圆的左、右焦点分别为、 , 过坐标原点的直线交椭圆于A、两点,点A在第一象限.
 (1)、若 , 求点A的坐标;(2)、求的取值范围;(3)、若轴,垂足为 , 连结并延长交椭圆于点 , 求面积的最大值.
(1)、若 , 求点A的坐标;(2)、求的取值范围;(3)、若轴,垂足为 , 连结并延长交椭圆于点 , 求面积的最大值. -
18、申辉中学为期两周的高一、高二年级校园篮球赛告一段落.高一小、高二小分别荣获了高一年级和高二年级比赛的年级MVP(最有价值球员).以下是他们在各自8场比赛的二分球和三分球出手次数及其命中率.
二分球出手
二分球命中率
三分球出手
三分球命中率
小
100次
100次
小
190次
10次
现以两人的总投篮命中率(二分球+三分球)较高者评为校(总投篮命中率总命中次数÷总出手次数)
(1)、小认为,目测小的二分球命中率和三分球命中率均高于小 , 此次必定能评为校 , 试通过计算判断小的想法是否准确?(2)、小是游戏爱好者,设置了一款由游戏人物小、小轮流投篮对战游戏,游戏规则如下:①游戏中小的命中率始终为0.4,小的命中率始终为0.3,②游戏中投篮总次数最多为次,且同一个游戏人物不允许连续技篮.③游戏中若投篮命中,则游戏结束,投中者获得胜利;若直至第次投篮都没有命中,则规定第二次投篮者获胜.若每次游戏对战前必须设置“第一次投篮人物”和“”的值,请解答以下两个问题.(ⅰ)若小第一次投篮,请证明小获胜概率大;
(ⅱ)若小第一次投篮,试问谁的获胜概率大?并说明理由.
-
19、如图,已知为圆柱底面圆的直径, , 母线长为3,点为底面圆的圆周上一点.
 (1)、若 , 求三棱锥的体积;(2)、若 , 求异面直线与所成的角的余弦值.
(1)、若 , 求三棱锥的体积;(2)、若 , 求异面直线与所成的角的余弦值. -
20、已知函数的表达式为 , .(1)、若函数的最小正周期为 , 求的值及的单调增区间;(2)、若 , 设函数的表达式为 , 求当时,的值域.