版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知函数 $f (x) = | x - 1 |$ ．
$(1)$ 解不等式 $f (2 x) + f (x + 4) \geq 6$ ；
$(2)$ 若a、 $b \in R$ ， $| a | < 1$ ， $| b | < 1$ ，证明： $f (a b) > f (a - b + 1)$ ．

查看解析
2、选修4-4：坐标系与参数方程
在平面直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 $\{\begin{array}{l} x = - 2 + \frac{1}{2} t \\ y = \frac{\sqrt{3}}{2} t \end{array}$ (t为参数) ，以坐标原点为极点， $x$ 轴正半轴为极轴，建立极坐标系，曲线 $C_{1}$ 的极坐标方程为 $ρ = \sqrt{6}$ .

(1)、写出直线 $l$ 的普通方程和曲线 $C_{1}$ 的参数方程；

(2)、若将曲线 $C_{1}$ 上各点的横坐标缩短为原来的 $\frac{\sqrt{6}}{6}$ 倍，纵坐标缩短为原来的 $\frac{\sqrt{2}}{2}$ 倍，得到曲线 $C_{2}$ ，设点 $P$ 是曲线 $C_{2}$ 上任意一点，求点 $P$ 到直线 $l$ 距离的最小值.

查看解析
3、已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{5}}{5}$ ，以椭圆的顶点为顶点的四边形面积为 $4 \sqrt{5}$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、我们称圆心在椭圆 $C$ 上运动且半径为 $\frac{\sqrt{a^{2} + b^{2}}}{3}$ 的圆是椭圆 $C$ 的“环绕圆”.过原点 $O$ 作椭圆 $C$ 的“环绕圆”的两条切线，分别交椭圆 $C$ 于 $A, B$ 两点，若直线 $O A, O B$ 的斜率存在，并记为 $k_{1}, k_{2}$ ，求 $k_{1} k_{2}$ 的取值范围.

查看解析
4、已知平面 $α$ 与平面 $β$ 是空间中距离为1的两平行平面， $A B \subset α$ ， $C D \subset β$ ，且 $A B = C D = 2$ ， $A B$ 和 $C D$ 的夹角为 $60 °$ .

(1)、证明：四面体 $A B C D$ 的体积为定值；

(2)、已知异于 $C$ 、 $D$ 两点的动点 $P \in β$ ，且 $P$ 、 $A$ 、 $B$ 、 $C$ 、 $D$ 均在半径为 $\frac{\sqrt{5}}{2}$ 的球面上.求点 $P$ 到直线 $A B$ 的距离的取值范围.

查看解析
5、已知函数 $f (x) = a x^{2} - ln x, a \in R$ .

(1)、讨论函数 $f (x)$ 的单调性；

(2)、设 $a > 0, g (x) = f (x) + b x$ ，且 $x = 1$ 是 $g (x)$ 的极值点，证明： $2 b +ln a \leq 1 - 2 \ln 2$ .

查看解析
6、如图，在四边形 $A B C D$ 中，已知点C关于直线BD的对称点 $C'$ 在直线AD上， $∠ C B D = ∠ C D B = 30 °$ ， $∠ A C D = 75 °$ ．

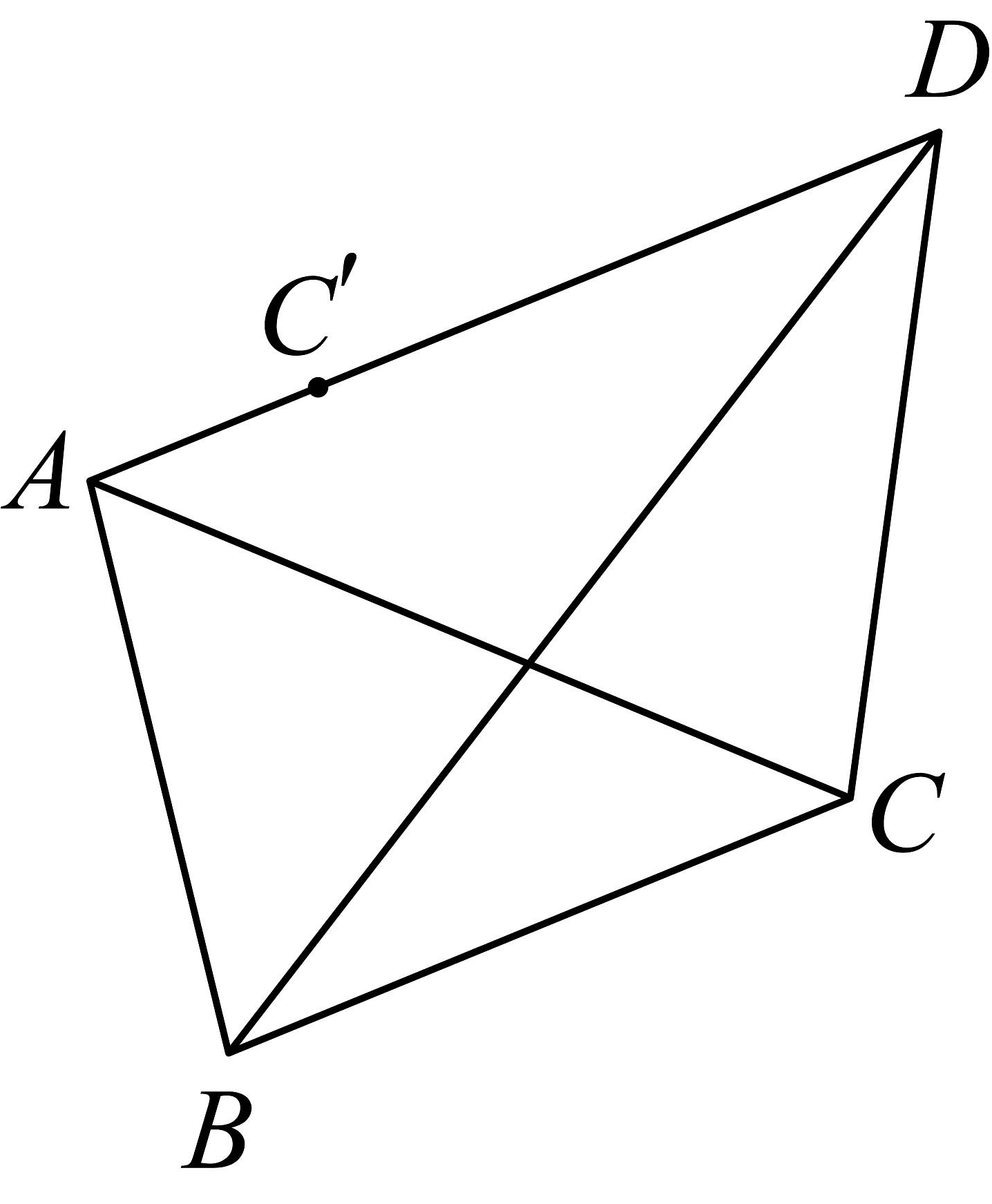(1)、求 $\frac{\sin ∠ B A C}{\sin ∠ A B C}$ 的值；

(2)、设AC=3，求 $A B^{2}$ ．

查看解析
7、成都石室中学生物基地里种植了一种观赏花卉，这种观赏花卉的高度（单位：cm）介于 $[15, 25]$ 之间，现对生物基地里部分该种观赏花卉的高度进行测量，所得数据统计如下图所示.

(1)、求 $a$ 的值；

(2)、若从高度在 $[15, 17)$ 和 $[17, 19)$ 中分层抽样抽取5株，再在这5株中随机抽取2株，求抽取的2株高度均在 $[17, 19)$ 内的概率.

查看解析
8、已知函数 $f (x)$ 的定义域为 $R$ ，对于任意实数 $x, y$ 均满足 $f (\frac{x + 2 y}{3}) = \frac{f (x) + 2 f (y)}{3}$ ，若 $f (2) = 1$ ， $f (5) = 10$ ，则 $f (724) =$ .

查看解析
9、若复数 $z = \frac{1}{2} + \frac{\sqrt{3}}{2} i$ （ $i$ 为虚数单位），则 $\bar{z} \cdot z^{2} =$ .

查看解析
10、若存在 $(x, y)$ 满足 $\{\begin{array}{l} 2 x - 3 y + 10 > 0 \\ x + 2 y - 9 > 0 \\ 3 x - y - 6 < 0 \end{array}$ ，且使得等式 $3 x + a (2 y - 4 e x) (\ln y - \ln x) = 0$ 成立，其中 $e$ 为自然对数的底数，则实数 $a$ 的取值范围是（）

A、 $(- \infty, 0) \cup [\frac{3}{2 e}, + \infty)$ B、 $[\frac{3}{2 e}, + \infty)$ C、 $(- \infty, 0)$ D、 $(0, \frac{3}{2 e}]$

查看解析
11、如图，射线 $l$ 与圆 $C : {(x - 1)}^{2} + {(y - 1)}^{2} = 1$ ，当射线 $l$ 从 $l_{0}$ 开始在平面上按逆时针方向绕着原点 $O$ 匀速旋转（ $A$ 、 $B$ 分别为 $l_{0}$ 和 $l$ 上的点，转动角度 $α = ∠ A O B$ 不超过 $\frac{π}{4}$ ）时，它被圆 $C$ 截得的线段 $E F$ 长度为 $L (α)$ ，则函数 $L (α)$ 的解析式为（）

A、 $L (α) = \frac{2 cos 2 α}{\sqrt{sin 2 α}}$ B、 $L (α) = 2 \sqrt{cos 2 α}$ C、 $L (α) = 2 \sqrt{sin 2 α}$ D、 $L (α) = \frac{cos 2 α}{\sqrt{sin 2 α}}$

查看解析
12、在平面直角坐标系 $x O y$ 中，点 $A (- 1, 0), B (2, 3)$ ，向量 $\vec{O C} = m \vec{O A} + n \vec{O B}$ ，且 $m - n - 4 = 0$ .若点 $C$ 的轨迹与双曲线 $\frac{x^{2}}{2} - y^{2} = 1$ 的渐近线相交于两点 $P$ 和 $Q$ （点 $P$ 在 $x$ 轴上方），双曲线右焦点为 $F$ ，则 $\frac{S_{△ P O F}}{S_{△ Q O F}} =$ （）

A、 $3 + 2 \sqrt{2}$ B、 $3 - 2 \sqrt{2}$ C、 $\frac{19 + 6 \sqrt{2}}{17}$ D、 $\frac{19 - 6 \sqrt{2}}{17}$

查看解析
13、甲、乙两艘轮船都要在某个泊位停靠6小时，假定它们在一昼夜的时间段中随机地到达，则这两艘船中至少有一艘在停靠泊位时必须等待的概率为（）

A、 $\frac{3}{16}$ B、 $\frac{13}{16}$ C、 $\frac{7}{16}$ D、 $\frac{9}{16}$

查看解析
14、佩香囊是端午节传统习俗之一，香囊内通常填充一些中草药，有清香、驱虫、开窍的功效.因地方习俗的差异，香囊常用丝布做成各种不同的形状，形形色色，玲珑夺目.图1的 $▱ A B C D$ 由六个正三角形构成，将它沿虚线折起来，可得图2所示的六面体形状的香囊，那么在图2这个六面体中，棱AB与CD所在直线的位置关系为（）

A、平行 B、相交 C、异面且垂直 D、异面且不垂直

查看解析
15、已知函数 $f (x) = x^{2} + 2 \ln x$ 的图象在 $A (x_{1}, f (x_{1})), B (x_{2}, f (x_{2}))$ 两个不同点处的切线相互平行，则 $x_{1} + x_{2}$ 的取值可以为（）

A、 $\frac{1}{4}$ B、1 C、2 D、 $\frac{10}{3}$

查看解析
16、物理学家本·福特提出的定律：在b进制的大量随机数据中，以n开头的数出现的概率为 $P_{b} (n) = \log_{b} \frac{n + 1}{n}$ .应用此定律可以检测某些经济数据、选举数据是否存在造假或错误.若 $\sum_{n = k}^{80} P_{10} (n) = \frac{\log_{4} 81}{1 + \log_{2} 5} (k \in N^{*})$ ，则k的值为（）

A、7 B、8 C、9 D、10

查看解析
17、已知函数 $f (x) = |\sin x \cos x + \frac{1}{4}|$ ，则下列说法正确的是（）

A、 $f (x)$ 的图象关于直线 $x = \frac{π}{2}$ 对称 B、 $f (x)$ 的周期为 $π$ C、 $(π, \frac{1}{4})$ 是 $f (x)$ 的一个对称中心 D、 $f (x)$ 在区间 $[\frac{π}{4}, \frac{π}{2}]$ 上单调递增

查看解析
18、如图是某赛季甲、乙两名篮球运动员5场比赛得分的茎叶图，已知甲的成绩的极差为31，乙的成绩的平均值为24，则下列结论错误的是（）

A、 $x = 9$ B、 $y = 6$ C、乙的成绩的中位数为 $28$ D、乙的成绩的方差小于甲的成绩的方差

查看解析
19、在 $△ A B C$ 中，“ $∠ A C B$ 是钝角”是“ $|\vec{C A} + \vec{C B}| < |\vec{A B}|$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看解析
20、某校高一、高二、高三的人数之比为 $9 : 7 : 4$ ，从中随机抽取400名学生组成志愿者，若学校中每人被抽中的概率都是 $\frac{1}{5}$ ，则该校高二年级的人数为（）

A、1000 B、900 C、800 D、700

查看解析

上一页 741 742 743 744 745 下一页跳转