相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、世界人口在过去年翻了一番,则每年人口平均增长率约是( )(参考数据,)A、 B、 C、 D、
-
2、不等式成立是不等式成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
3、有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
-
4、已知.(1)、若展开式的第3项和第5项的二项式系数相等,求的值,并求常数项;(2)、若展开式中所有项的系数之和为81,求展开式中二项式系数最大的项.
-
5、已知 , 则.
-
6、现有4名男生和3名女生计划利用假期到某地景区旅游,由于是旅游的旺季,他们在景区附近订购了一家酒店的5间风格不同的房间,并约定每个房间都要住人,每个房间最多住2人,且男女不能混住.则不同的安排方法有( )种A、1960 B、2160 C、2520 D、2880
-
7、某体育器材厂生产一批篮球,单个篮球的质量(单位:克)服从正态分布 , 从这一批篮球中随机抽检300个,则被抽检的篮球的质量不小于596克的个数约为( )A、246 B、252 C、286 D、293
-
8、函数在内恰有两个对称中心, , 将函数的图象向右平移个单位得到函数的图象.若 , 则( )A、 B、 C、 D、
-
9、函数的部分图象大致是( )A、
 B、
B、 C、
C、 D、
D、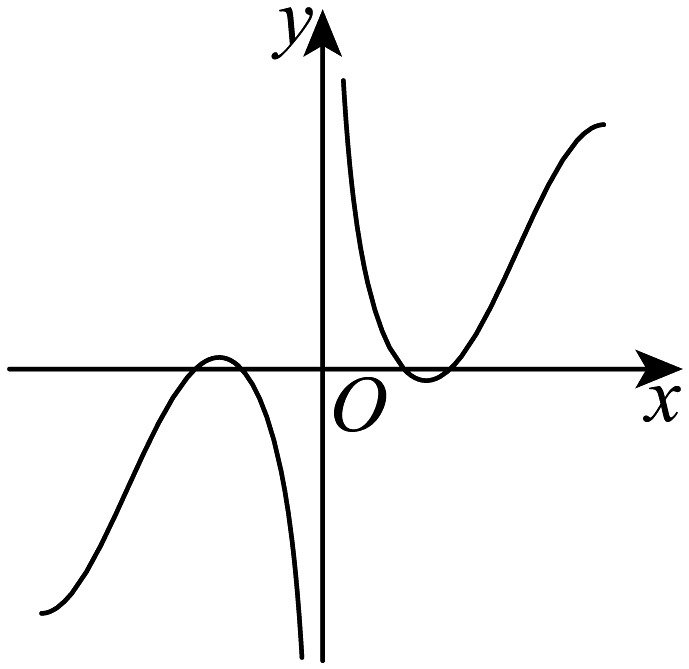
-
10、若直线与圆O:相切,则圆与圆O( )A、相离 B、相交 C、内切 D、外切
-
11、在中,角的对边分别是 , 且.(1)、求角;(2)、若的角平分线交于点 , 求.
-
12、已知函数是定义在R上的奇函数.(1)、求的值,并用定义证明的单调性;(2)、若时,不等式有解,求实数的取值范围.(3)、若对任意的时,不等式恒成立,求实数的取值范围.
-
13、在ΔABC中,P为AB的中点,O在边AC上,BO交CP于R,且 , 设AB= , AC=
 (1)、试用 , 表示;(2)、若 , 求∠ARB的余弦值(3)、若H在BC上,且RH⊥BC设 , 若 , 求的范围.
(1)、试用 , 表示;(2)、若 , 求∠ARB的余弦值(3)、若H在BC上,且RH⊥BC设 , 若 , 求的范围. -
14、已知函数(1)、求的最小正周期和对称轴;(2)、求在上的单调递增区间.
-
15、(1)已知的坐标分别是 , 求的坐标.
(2)已知 , , 与的夹角为 , 求
-
16、已知 , 求的值.
-
17、已知向量满足 , , , , 则的最小值是 .
-
18、已知 , 则.
-
19、已知角的终边经过点 , 则的值为 .
-
20、已知函数 , 则下列描述正确的是( )A、函数的最小正周期为 B、是函数图象的一个对称轴 C、是函数图象的一个对称中心 D、若函数的图象向左平移个单位长度可得函数的图象,则为奇函数