相关试卷
- 河北省张家口市2016-2017学年高一下学期数学期末考试试卷
- 河北省邢台市2016-2017学年高一下学期数学期末考试试卷
- 河北省唐山市2016-2017学年高一下学期数学期末考试试卷
- 河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷
- 河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷
- 河北省邯郸市2016-2017学年高一下学期数学期末考试试卷
- 河北省承德市2016-2017学年高一下学期数学期末考试试卷
- 河北省保定市2016-2017学年高一下学期数学期末考试试卷
- 江西省赣州市2016-2017学年高一下学期期末数学考试试卷
- 四川省雅安市2016-2017学年高二下学期数学期末考试试卷(文科)
-
1、已知函数 , , 的零点分别为 , , , 则 , , 的大小顺序为( )A、 B、 C、 D、
-
2、函数的部分图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
3、下列不等关系成立的是( )A、 B、 C、 D、
-
4、“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
5、已知幂函数的图象过点 , 则( )A、 B、 C、2 D、3
-
6、已知集合 , , 则( )A、 B、 C、 D、
-
7、设 , , 定义:为 , 的最大公约数,为 , 的最小公倍数,且具有以下性质:①;②当时,.(1)、已知数列 , 的通项公式分别为 , , 其中 , 令 , 求数列的通项公式;(2)、已知有限数列满足 , 且(为给定常数).若对 , 且( , )时,都有.
(ⅰ)当时,证明:;
(ⅱ)证明:.
-
8、已知点是椭圆:()上一点,的焦距为2.(1)、求的方程;(2)、过的右焦点作斜率不为0的直线 , 交于 , 两点, , 是的左、右顶点,记直线 , 的斜率分别为 , .
(ⅰ)求的值;
(ⅱ)设为直线与直线的交点,记的面积为 , 的面积为 , 求的最小值.
-
9、已知函数().(1)、当时,求曲线在点处的切线方程;(2)、若 , 求的取值范围.
-
10、如图,在四棱锥中, , , , 侧面是正三角形,侧面底面 , 是的中点.
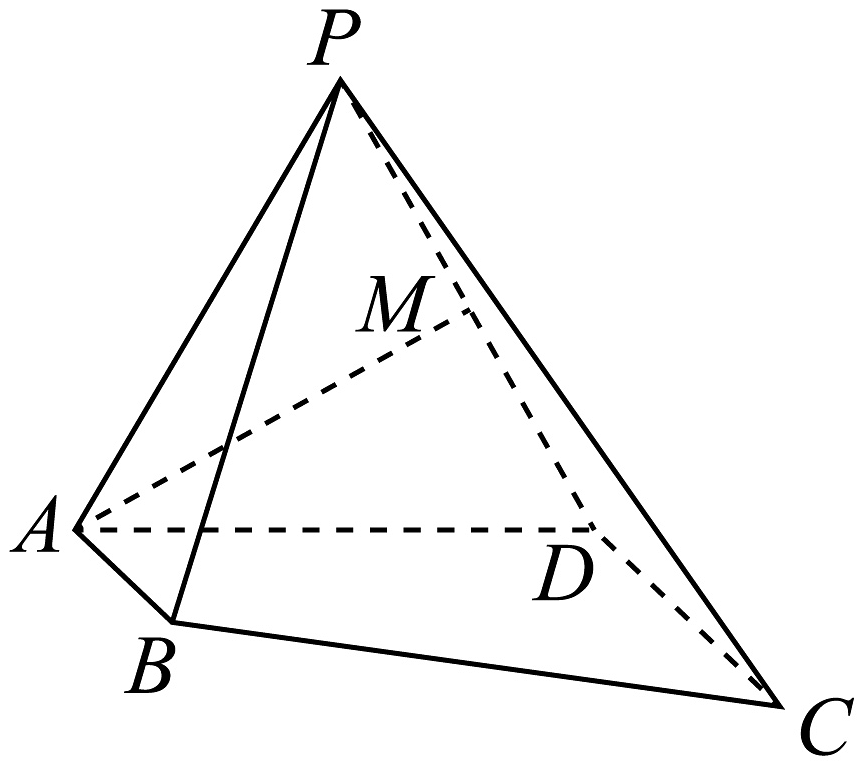 (1)、求证:平面;(2)、求平面与平面的夹角的余弦值.
(1)、求证:平面;(2)、求平面与平面的夹角的余弦值. -
11、甲、乙两选手进行乒乓球比赛,采用5局3胜制,假设每局比赛甲获胜的概率为 , 乙获胜的概率为 , 且每局比赛结果相互独立.(1)、求赛完4局且乙获胜的概率;(2)、若规定每局获胜者得2分,负者得分,记比赛结束时甲最终得分为 , 求的分布列和数学期望.
-
12、已知 , 是双曲线:( , )的左、右焦点,过作斜率为的直线交于点 , 且在第一象限,若(为坐标原点),则的离心率为.
-
13、已知 , 则.(用数字作答)
-
14、已知函数 , 则的最小正周期为.
-
15、胆式瓶创于南宋龙泉窑,康熙时期以郎红釉胆式瓶为贵.如图是18世纪的窑变红釉胆瓶,其优美的造型可看作图中曲线的一部分.已知曲线上的点到的距离与到轴的距离之积为6,若曲线上的点在第一象限,则( )
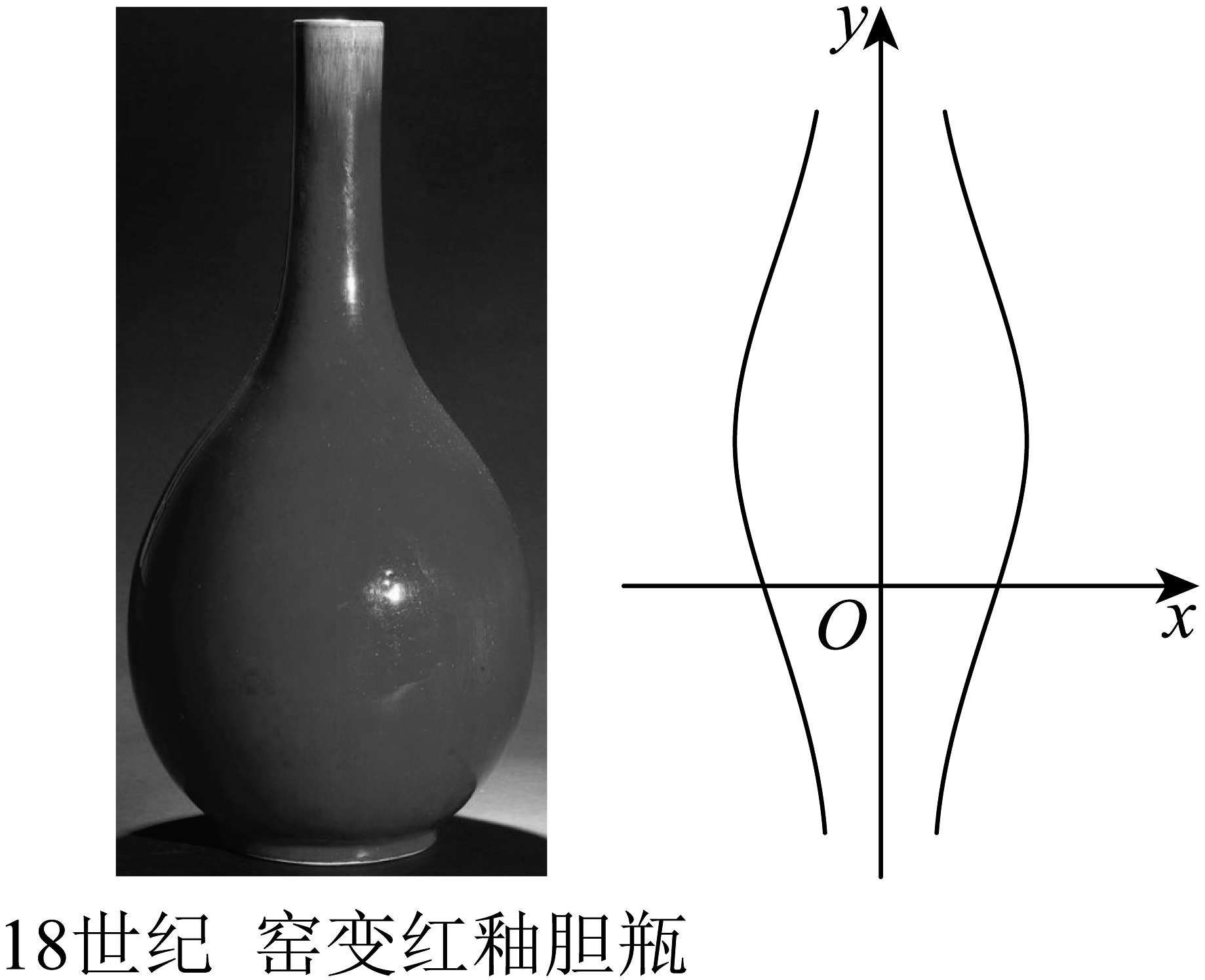 A、的最大值为 B、 C、曲线的内接矩形的面积最大值为24 D、一个胆式瓶的剖面图可近似看作曲线(),若一正四面体可在胆式瓶内任意转动(忽略胆式瓶的厚度),则该正四面体棱长的最大值为4
A、的最大值为 B、 C、曲线的内接矩形的面积最大值为24 D、一个胆式瓶的剖面图可近似看作曲线(),若一正四面体可在胆式瓶内任意转动(忽略胆式瓶的厚度),则该正四面体棱长的最大值为4 -
16、已知函数 , 则( )A、当时, B、当时, C、当且时, D、当且时,
-
17、已知直线:和圆: , 则( )A、当与圆相切时, B、当为圆的一条对称轴时, C、当时,与圆没有公共点 D、当时,被圆截得的弦长为
-
18、已知 , 则( )A、 B、 C、 D、
-
19、已知正四面体的棱长为2,点是的中点,点在正四面体表面上运动,并且总保持 , 则动点的轨迹周长为( )A、4 B、 C、 D、
-
20、已知函数是奇函数,则( )A、2 B、1 C、 D、