-
1、设甲袋有3个红球,2个白球和5个黑球,乙袋有3个红球,3个白球和4个黑球,先从甲袋中随机取出一球放入乙袋,以、和分别表示由甲袋取出的球是红球、白球和黑球的事件;再从乙袋中随机取出一球,以B表示由乙袋取出的球是红球的事件,则( )A、与B相互独立 B、 C、 D、
-
2、如果圆与圆关于直线l对称,则直线l的方程为( )A、 B、 C、或 D、
-
3、设 , 若函数在内存在极值点,则a的取值范围是( )A、 B、 C、 D、
-
4、若圆锥的侧面展开图是半径为3,圆心角为的扇形,则该圆锥的体积为( )A、 B、 C、 D、
-
5、在的展开式中,含的项的系数是( )A、 B、 C、 D、
-
6、要得到函数的图象,只要将函数的图象( )A、向右平移个单位 B、向左平移个单位 C、向右平移个单位 D、向左平移个单位
-
7、“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件
-
8、已知 , , , 则的最大值为( )A、1 B、2 C、4 D、不存在
-
9、在中, , , 若是的中点 , 则;若是的一个三等分点 , 则;若是的一个四等分点 , 则
 (1)、如图①,若 , 用 , 表示 , 你能得出什么结论?并加以证明.(2)、如图②,若 , , 与交于 , 过点的直线与 , 分别交于点 , .
(1)、如图①,若 , 用 , 表示 , 你能得出什么结论?并加以证明.(2)、如图②,若 , , 与交于 , 过点的直线与 , 分别交于点 , .①利用(1)的结论,用 , 表示;
②设 , , 求的最小值.
-
10、在中,角A,B,C所对的边分别为a,b,c,若 , 则的形状为( )A、直角三角形 B、等腰三角形 C、等腰直角三角形 D、直角三角形或等腰三角形
-
11、如图,正方形的边长为分别为边上的动点,若为的中点,且满足 , 则的最小值为( )
 A、 B、4 C、 D、8
A、 B、4 C、 D、8 -
12、在中,已知 , 则等于( )A、 B、 C、 D、
-
13、已知向量 , 若 , 则( )A、 B、 C、 D、
-
14、已知某人每次投篮的命中率为 , 投进一球得1分,投不进得0分,记投篮一次的得分为X,则的最大值为 .
-
15、已知复数满足 , 其中是虚数单位,则( )A、 B、 C、 D、
-
16、已知点A,B分别是双曲线的上、下顶点,点P满足 .(1)、求点P的轨迹方程;(2)、是否存在点P,使得过点P的动直线l交双曲线C于M,N两点,且与的斜率之和为定值?若存在,求点P的坐标;若不存在,请说明理由.
-
17、如图,在四棱锥中, , 点Q为棱上一点.
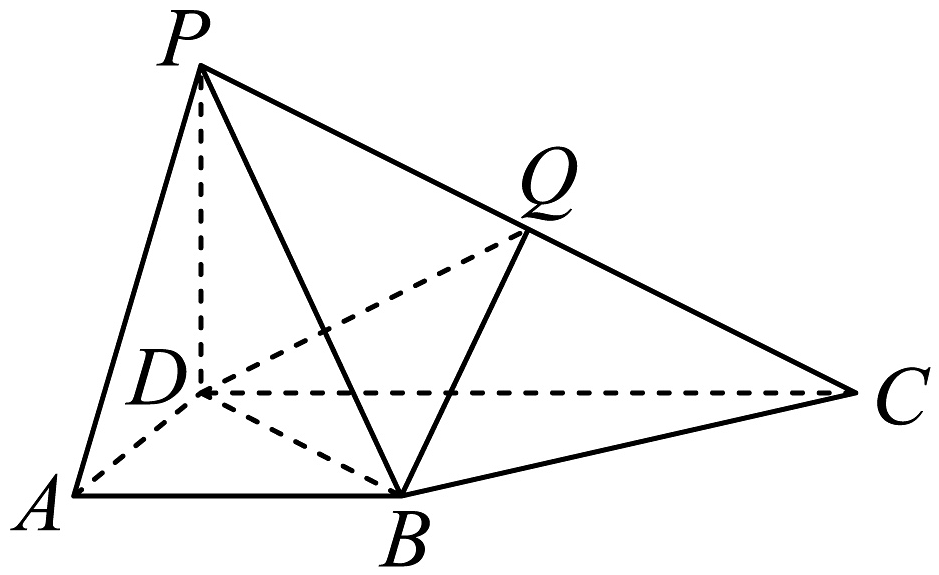 (1)、证明:平面;(2)、当点Q为棱的中点时,求直线与平面所成角的正弦值;(3)、当二面角的余弦值为时,求 .
(1)、证明:平面;(2)、当点Q为棱的中点时,求直线与平面所成角的正弦值;(3)、当二面角的余弦值为时,求 . -
18、已知数列满足 .(1)、求的通项公式;(2)、已知 , 求数列的前n项和 .
-
19、已知函数 , 且 .(1)、求a的值;(2)、若 , 求的值.
-
20、已知函数及点 .(1)、若点P在的图象上,求曲线在点P处的切线的方程;(2)、若点P在的图象外,过点P与的图象相切的直线斜率是1,求a的取值.