2017-2018学年北师大版高考数学模拟试卷
试卷更新日期:2018-02-25 类型:高考模拟
一、单选题
-
1. 已知集合A={1,3, },B={1,m},A∪B=A,则m=( )A、0或 B、0或3 C、3或 D、1或32. 已知集合A={3,a2},集合B={0,b,1﹣a},且A∩B={1},则A∪B=( )A、{0,1,3} B、{1,2,4} C、{0,1,2,3} D、{0,1,2,3,4}3. 函数f(x)= 的图象与函数g(x)=log2(x+a)(a∈R)的图象恰有一个交点,则实数a的取值范围是( )A、a>1 B、a≤﹣ C、a≥1或a<﹣ D、a>1或a≤﹣4. 已知函数f(x)= ,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )A、(4,2018) B、(4,2020) C、(3,2020) D、(2,2020)5. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”问此人第4天和第5天共走了( )A、60里 B、48里 C、36里 D、24里6. 若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数与其图象相符的是( )
 A、
A、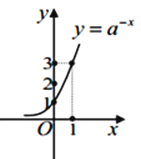 B、
B、 C、
C、 D、
D、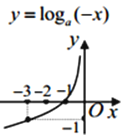 7. 已知f(x)是定义在(0,3)上的函数,f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( )
7. 已知f(x)是定义在(0,3)上的函数,f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( )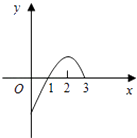 A、(0,1)∪(2,3) B、 C、 D、(0,1)∪(1,3)8. 已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有 ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )A、0<a≤5 B、a<5 C、0<a<5 D、a≥59. 函数f(x)=(x﹣2)(ax+b)为偶函数,且在(0,+∞)单调递增,则f(2﹣x)>0的解集为( )A、{x|x>2或x<﹣2} B、{x|﹣2<x<2} C、{x|x<0或x>4} D、{x|0<x<4}10. 已知x,y∈R,且 ,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )A、4 ﹣ B、4 ﹣ C、 D、 +11. 在△ABC中,P、Q分别在AB,BC上,且 = , = ,若 = , = ,则 =( )A、 + B、﹣ + C、 ﹣ D、﹣ ﹣12. 设A是双曲线 的右顶点,F(c,0)是右焦点,若抛物线 的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )A、[2,+∞) B、(1,2] C、(1,3] D、[3,+∞)
A、(0,1)∪(2,3) B、 C、 D、(0,1)∪(1,3)8. 已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有 ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在区间(0,3]上有两解,则实数a的取值范围是( )A、0<a≤5 B、a<5 C、0<a<5 D、a≥59. 函数f(x)=(x﹣2)(ax+b)为偶函数,且在(0,+∞)单调递增,则f(2﹣x)>0的解集为( )A、{x|x>2或x<﹣2} B、{x|﹣2<x<2} C、{x|x<0或x>4} D、{x|0<x<4}10. 已知x,y∈R,且 ,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )A、4 ﹣ B、4 ﹣ C、 D、 +11. 在△ABC中,P、Q分别在AB,BC上,且 = , = ,若 = , = ,则 =( )A、 + B、﹣ + C、 ﹣ D、﹣ ﹣12. 设A是双曲线 的右顶点,F(c,0)是右焦点,若抛物线 的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )A、[2,+∞) B、(1,2] C、(1,3] D、[3,+∞)二、填空题
-
13. 设抛物线y2=4x的焦点为F,过点F作直线l与抛物线分别交于两点A,B,若点M满足 = ( + ),过M作y轴的垂线与抛物线交于点P,若|PF|=2,则M点的横坐标为 .14. 如图,抛物线y2=4x的一条弦AB经过焦点F,取线段OB的中点D,延长OA至点C,使|OA|=|AC|,过点C,D作y轴的垂线,垂足分别为E,G,则|EG|的最小值为 .
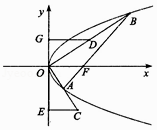 15. 如图是一个算法的流程图,则输出的n的值是 .
15. 如图是一个算法的流程图,则输出的n的值是 .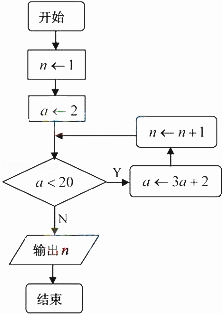 16. 已知关于空间两条不同直线m,n,两个不同平面α,β,有下列四个命题:①若m∥α且n∥α,则m∥n;②若m⊥β且m⊥n,则n∥β;③若m⊥α且m∥β,则α⊥β;④若n⊂α且m不垂直于α,则m不垂直于n.其中正确命题的序号为 .
16. 已知关于空间两条不同直线m,n,两个不同平面α,β,有下列四个命题:①若m∥α且n∥α,则m∥n;②若m⊥β且m⊥n,则n∥β;③若m⊥α且m∥β,则α⊥β;④若n⊂α且m不垂直于α,则m不垂直于n.其中正确命题的序号为 .三、综合题
-
17. 函数f(x)=loga(1﹣x)+loga(x+3),(0<a<1).(1)、求函数f(x)的定义域;(2)、若函数f(x)的最小值为﹣2,求a的值.18. 已知函数f(x)=lnx,g(x)= ﹣ (x为实常数).(1)、当a=1时,求函数φ(x)=f(x)﹣g(x)在x∈[4,+∞)上的最小值;(2)、若方程e2f(x)=g(x)(其中e=2.71828…)在区间[ ]上有解,求实数a的取值范围.19. 已知在△ABC中,角A,B,C的对边分别为a,b,c,且asinB+bcosA=0.(1)、求角A的大小;(2)、若 ,求△ABC的面积.20. 已知离心率为 的椭圆C: + =1(a>b>0)过点P(﹣1, ).(1)、求椭圆C的方程;(2)、直线AB:y=k(x+1)交椭圆C于A、B两点,交直线l:x=m于点M,设直线PA、PB、PM的斜率依次为k1、k2、k3 , 问是否存在实数t,使得k1+k2=tk3?若存在,求出实数t的值以及直线l的方程;若不存在,请说明理由.21. 如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
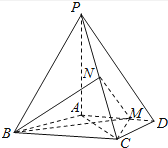 (1)、证明:MN∥平面PAB;(2)、求直线AN与平面PMN所成角的正弦值.
(1)、证明:MN∥平面PAB;(2)、求直线AN与平面PMN所成角的正弦值.