-
1、在中,角A,B,C所对应的边分别为a,b,c.已知.
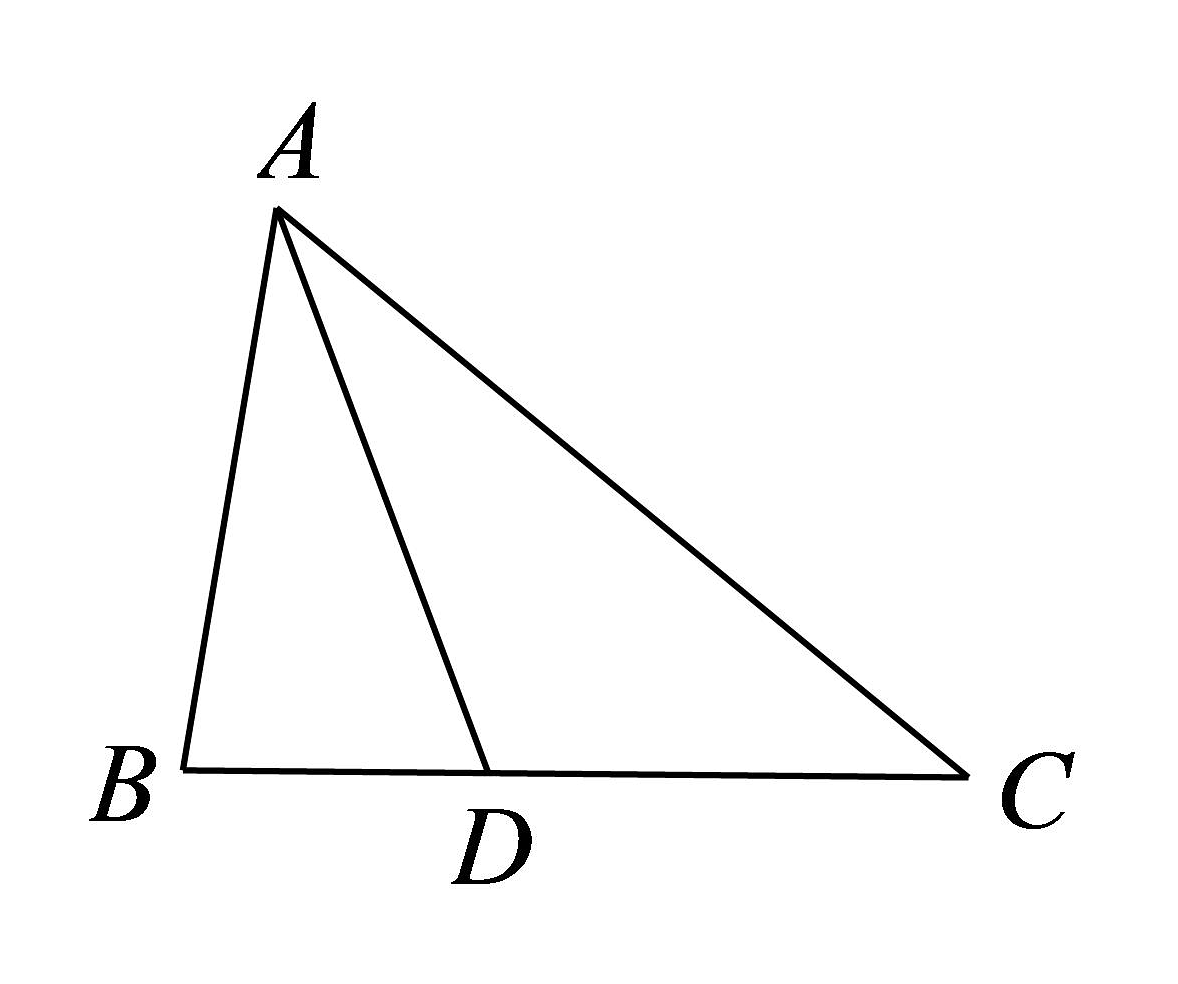 (1)、求角A;(2)、若 , , 求的周长;(3)、如图,的平分线交于点 , , 求的取值范围.
(1)、求角A;(2)、若 , , 求的周长;(3)、如图,的平分线交于点 , , 求的取值范围. -
2、已知函数的部分图象如图所示.
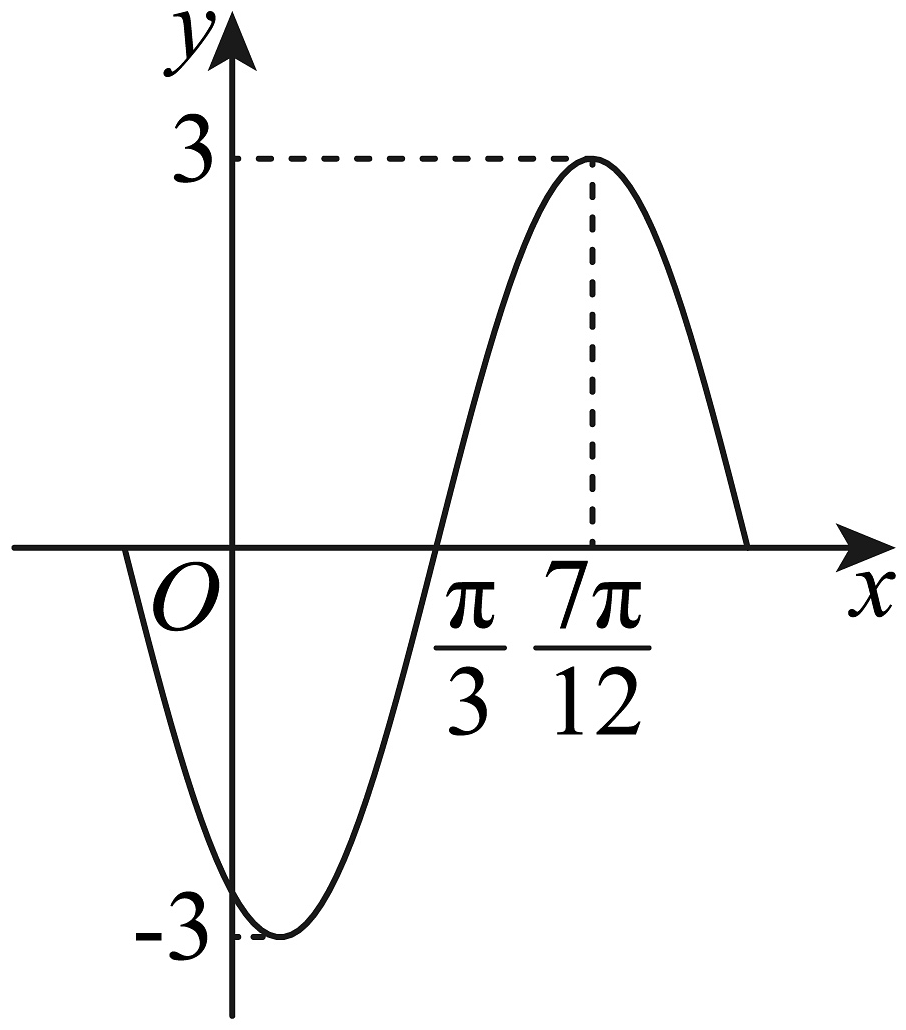 (1)、求的解析式及单调递增区间;(2)、将函数的图象向左平移个单位长度后得到函数图象,若不等式对任意成立,求m的取值范围.
(1)、求的解析式及单调递增区间;(2)、将函数的图象向左平移个单位长度后得到函数图象,若不等式对任意成立,求m的取值范围. -
3、已知角的顶点在原点,始边与轴的非负半轴重合,终边经过点 , 且.(1)、求的值;(2)、将的终边按顺时针方向旋转 , 此时终边所对应的角为 , 求的值.
-
4、已知向量 , 的夹角为45°,且满足 , .(1)、求向量在向量上的投影长度;(2)、若向量与向量共线,求的值.
-
5、解放碑是重庆的标志建筑物之一,存在其特别的历史意义.我校数学兴趣小组为了测量其高度,设解放碑杯杯高为AB,在地面上共线的三点C,D,E处分别测得顶点A的仰角为 , 且 , 则解放碑的高AB为.
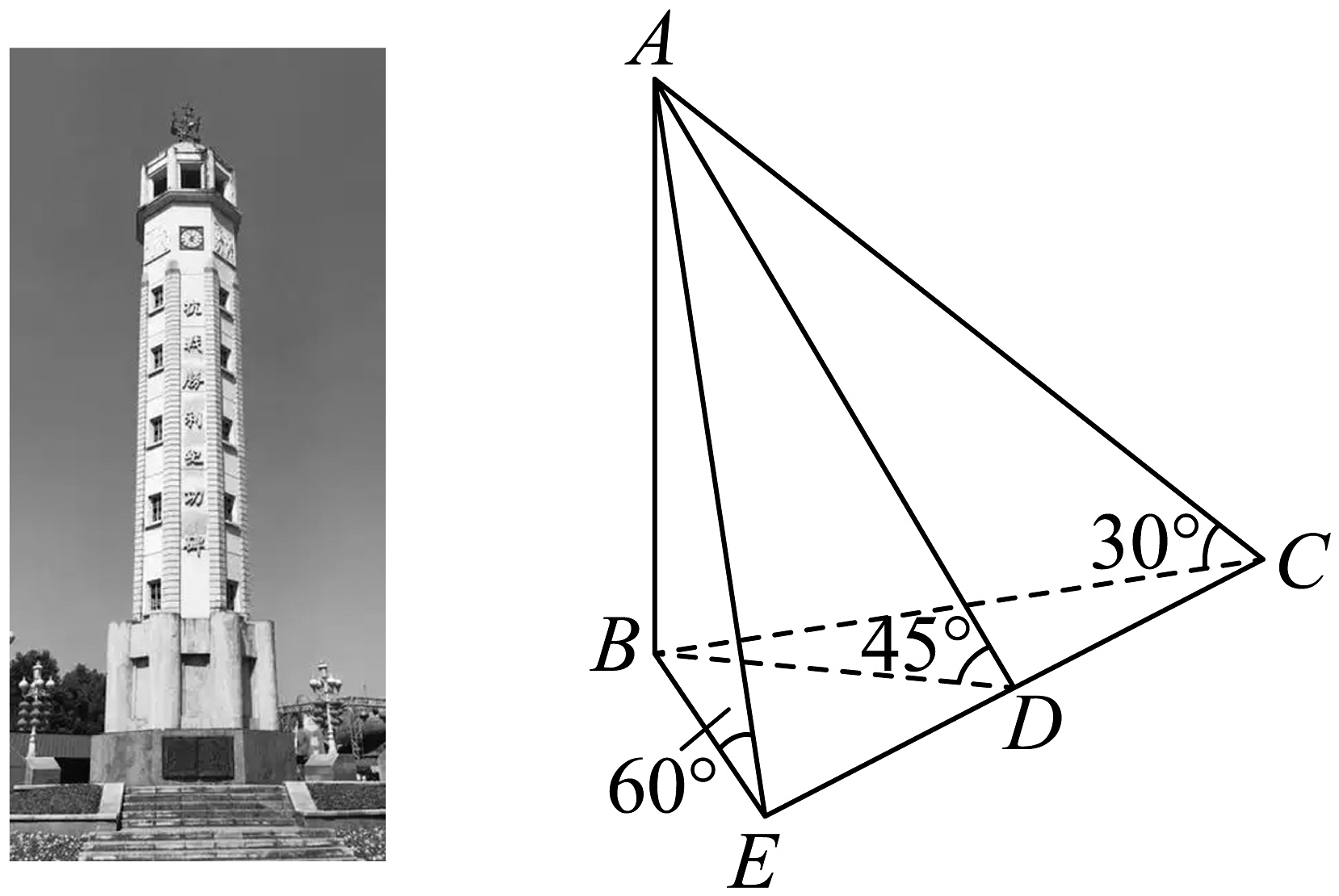
-
6、已知角 , 满足 , , 则.
-
7、已知圆锥的底面半径 , 高为 , 则这个圆锥的表面积是.
-
8、如图茶杯的形状是一个上宽下窄的正四棱台,上底面边长为下底面边长的2倍,容积为28mL,厚度忽略不计.当倒入14mL茶水时,茶水的高度与茶杯的高度之比为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9、的内角A,B,C的对边分别为 , , , , , 如果有两解,则的值可能为( )A、9 B、 C、11 D、12
-
10、一蜂巢的精密结构由7个边长均为2的正六边形组成,摆放位置如图所示,其中A,B,P为三个固定顶点,则( )
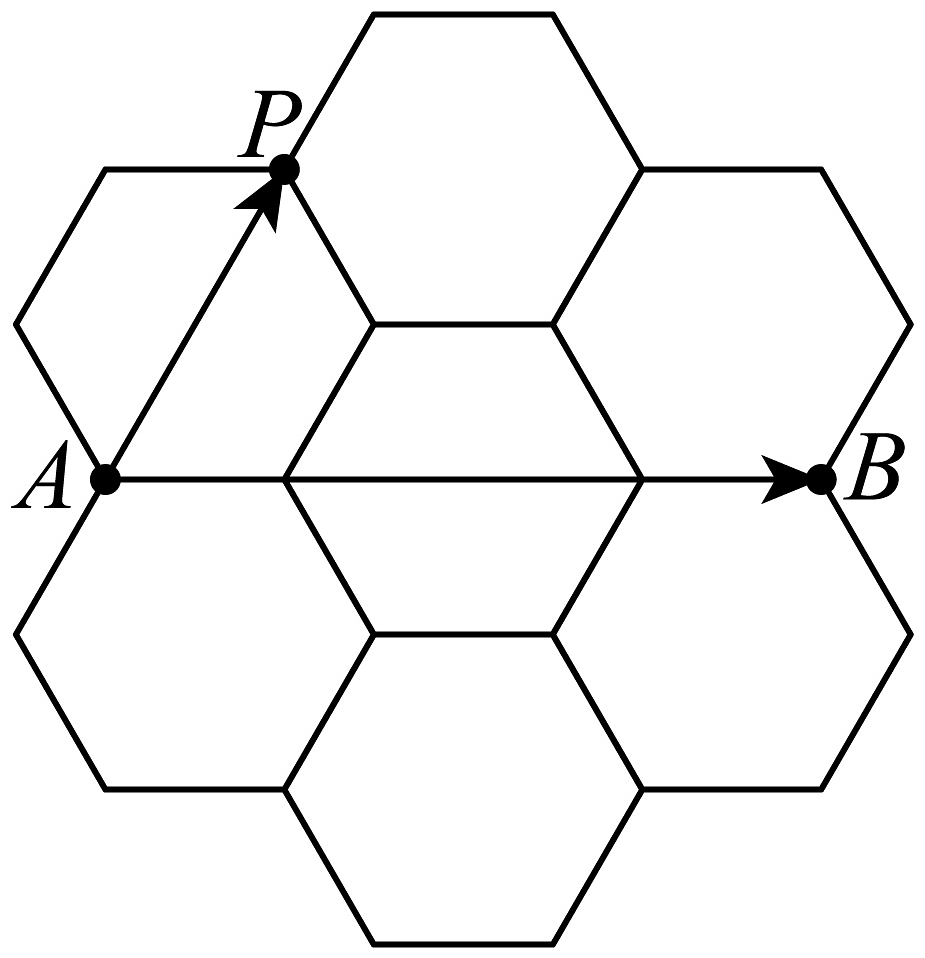 A、12 B、16 C、 D、
A、12 B、16 C、 D、 -
11、用斜二测法画水平放置的边长为的正三角形,所得直观图的面积为( )A、 B、 C、 D、
-
12、已知向量 , , , , , 则一定共线的三点是( )A、A,B,D B、A,B,C C、A,C,D D、B,C,D
-
13、下列函数中,最小正周期为且是奇函数的是( )A、 B、 C、 D、
-
14、已知扇形的弧长为 , 圆心角为40°,则该扇形的半径为( )A、2 B、3 C、6 D、8
-
15、若复数 , 则在复平面内对应的点所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
16、若数列( , , )满足 , 则称数列为k项数列,集合是由所有k项数列组成的集合,从集合中任意取出两个不同数列 , 记变量(1)、当时,求集合;(2)、若 , 求随机变量X的分布列与数学期望;(3)、求 , 其中且 .
-
17、已知椭圆C:()的左顶点为A,离心率为 , 且过点(1)、求椭圆C的方程;(2)、直线l与椭圆C交于M,N两点,点P为的外心.
①若为等边三角形,求PA的长;
②若点P在直线上,求点A到直线l距离的最大值.
-
18、已知函数 , 其中 .(1)、若在点处的切线与两坐标轴所围成三角形的面积为 , 求a的值;(2)、若是的极小值点,试比较与的大小.
-
19、在中,角所对的边分别为 , 已知 , 且 .(1)、若 , 求A;(2)、若是锐角三角形,求周长的取值范围.
-
20、已知数列满足 , 给出定义:使数列的前k项和为正整数的k()叫做好数,则在内的所有“好数”的和为 .