-
1、如图,四棱锥的底面是菱形,且平面 , E,F分别是棱PB,PC的中点.
 (1)、求证:平面PAD.(2)、求证:平面平面PAC.(3)、若 , 求直线DF和平面PAB所成角的正弦值.
(1)、求证:平面PAD.(2)、求证:平面平面PAC.(3)、若 , 求直线DF和平面PAB所成角的正弦值. -
2、中国新能源汽车产业发展势头迅猛,社会关注度持续增长.大数据显示,不同品牌的新能源汽车,其关注群体有不同的年龄分布.某网站面向关注新能源汽车的站内用户群体做了一个问卷调查,从关注品牌A的网友中随机抽取300人,并将他们按年龄分成了 , , , , (单位:岁)这五组,并画出频率分布直方图如图所示.
 (1)、求图中a的值和80%分位数(精确到小数点后一位);(2)、根据以上数据,估计该网站用户中关注新能源品牌A的网友的平均年龄.
(1)、求图中a的值和80%分位数(精确到小数点后一位);(2)、根据以上数据,估计该网站用户中关注新能源品牌A的网友的平均年龄. -
3、已知正实数x,y满足 , 则的取值范围.
-
4、已知正三角形ABC边长为12,点E为AB边的中点, , 若点P是边上的动点,则满足的点P有个
-
5、已知函数 , 如图,A,B是直线与曲线的两个交点,若 , 则.
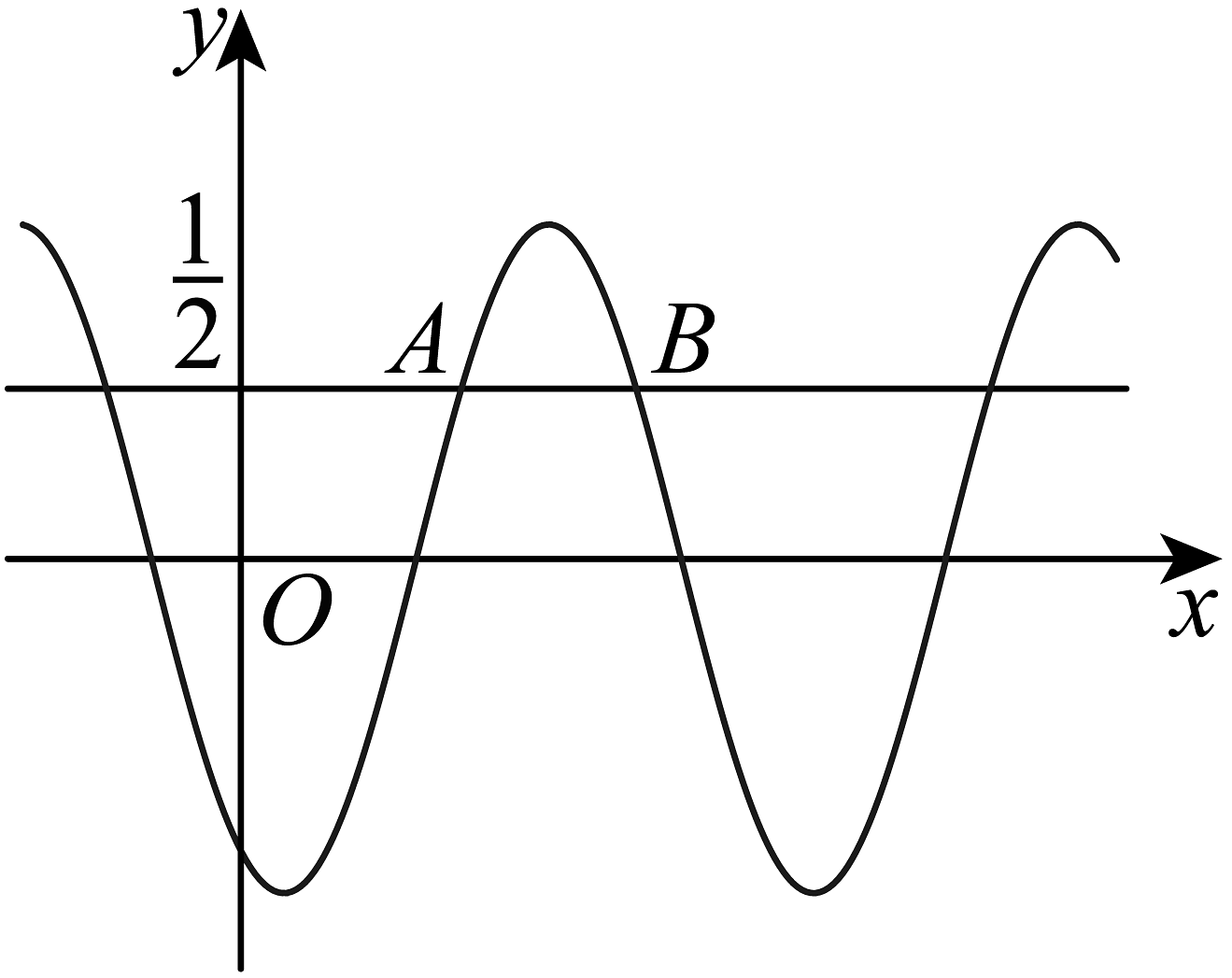
-
6、已知函数是奇函数,当时, , 则当时,.
-
7、已知正方体 , 棱长为1,点P是正方形内的动点(包括正方形边界),则( )A、若P到点 , 距离相等,则P的轨迹是线段 B、P到直线AB距离的最小值为 C、存在点P,使得二面角的大小为 D、若P是中点,则PA与平面ABCD所成角的正切值为
-
8、已知定义在R上的函数满足 , 且为奇函数,则( )A、4 B、 C、2 D、
-
9、石墨烯纳米材料的制备过程中,需通过激光散射技术监测纳米颗粒的团聚程度.在团聚指数增长阶段,散射光强度达到检测阈值时,颗粒团聚体数量与超声处理时间(单位:分钟)满足 , 其中为初始颗粒数量,为团聚速率常数.已知某样品经超声处理6分钟后,团聚体数量变为初始的100倍,则团聚速率常数约为( )(参考数据: , )A、56.2% B、77.8% C、115.4% D、118.4%
-
10、当时,下列不等式中正确的是( )A、 B、 C、 D、
-
11、异面直线a,b所成的角为 , 过空间一点P作直线l,使l与a,b所成的角均为 , 这样的直线条数为( )A、0 B、1 C、2 D、3
-
12、在中,角A,B,C所对的边分别是a,b,c, , 则( )A、 B、 C、 D、
-
13、已知一个正方体的顶点都在球面上,该球的体积为 , 则正方体的棱长为( )A、 B、 C、 D、
-
14、函数的值域是( )A、 B、 C、 D、
-
15、非零单位向量 , 满足 , 则与夹角是( )A、 B、 C、 D、
-
16、已知a,b为实数,则“”是“且”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
17、一个不透明盒子中装有4个红球和3个白球,这些球除颜色外无其它差别.从袋子中随机摸出一个球,则摸到红球的概率是( )A、 B、 C、 D、
-
18、复数 , 则的实部为( )A、3 B、 C、1 D、2
-
19、甲乙两名选手参加某球类比赛,比赛采用积分制:赛满奇数局,赢1局得2分,输者不得分,积分多者胜.已知甲选手每局比赛获胜的概率为 , 每局比赛的结果相互独立.(1)、若两人共进行了3局比赛,且 , 求甲最终获胜的概率及甲得分的方差;(2)、若两人共进行了局比赛,甲最终获胜的概率为 , 证明: , 并说明其统计意义.
-
20、已知函数 .(1)、讨论的单调性;(2)、若 , 求实数的取值范围;(3)、当时,若关于的方程有两个实根和 , 求证: .