-
1、计算:(1)、(2)、
-
2、计算:(1)、(2)、
-
3、如图,正方体表面展开图的相对的表面上所标的数都是互为相反数的两个数,那么图中的值是 .

-
4、如果股票指数上涨60点记作 , 那么股票指数下跌30点记作 .
-
5、已知x,a,b为互不相等的三个有理数,且 , 若式子的最小值为3,则的值为( ).A、2025 B、2026 C、2027 D、2028
-
6、若 , 且 , 则的值是( ).A、 B、12 C、或 D、2或12
-
7、下列有理数大小关系判断正确的是( )A、 B、 C、 D、
-
8、下列计算中,正确的是( )A、 B、 C、 D、
-
9、规定两数a,b之间的一种运算,记作::如果 , 那么
例如:因为 , 所以 .
(1)、根据上述规定,填空:______;(2)、若 , , 且 , 求的值;(3)、①若 , 请你尝试证明:;②进一步探究这种运算时发现一个结论: , 结合①,②探索的结论,计算:_____.
-
10、比较大小:(填“”、“”或“”).
-
11、如图所示, 已知 , 、分别平分和点E在上,请你探究线段与线段、之间的数量关系.
 (1)、用等式表示线段与线段、之间的数量关系: ;(2)、请你对第(1) 问中的数量关系进行证明.
(1)、用等式表示线段与线段、之间的数量关系: ;(2)、请你对第(1) 问中的数量关系进行证明. -
12、某学校在本学期开展数学拓展活动,为了解开展数学拓展活动后学生不同阶段的学习效果,决定随机抽取七年级部分学生进行两次跟踪测评(两次随机抽取的学生人数相同),第一次是开展数学拓展活动初期的学习质量测评,第二次是开展数学拓展活动个月后的学习质量测评.根据测评的数学成绩制作了第一次测评的数学成绩频数分布直方图(如图,每一组包括左边端点,不包括右边端点)和第二次测评的数学成绩频数分布表(如表).
第二次测评的数学成绩频数分布表:
成绩
频数
根据以上图表信息,完成下列问题:
第一次测评的数学成绩频数分布直方图

(1)______;
(2)若分及以上为优秀.
①开展数学拓展活动个月后,请估计该校名七年级学生数学成绩优秀的人数;
②请分别计算两次测评数学成绩的优秀率,并对开展数学拓展活动的效果进行分析.
-
13、小明在计算时,不小心把一个运算符号写错了(“”错写成“”或“”错写成“”),结果算成了 , 则原式从左往右数,第个运算符号写错了.
-
14、如图1,内接于 , , , 点E为上一点,点F为的中点,连结并延长与交于点G,连 , .
 (1)、求证: .(2)、如图2,当经过圆心O时,
(1)、求证: .(2)、如图2,当经过圆心O时,①求的长;
②记 , 的面积分别为 . 则 .
-
15、如图是由小正方形组成的网格.每个小正方形的顶点叫做格点,请用一把无刻度直尺及圆规借助网格根据要求作图,要求保留作图痕迹.
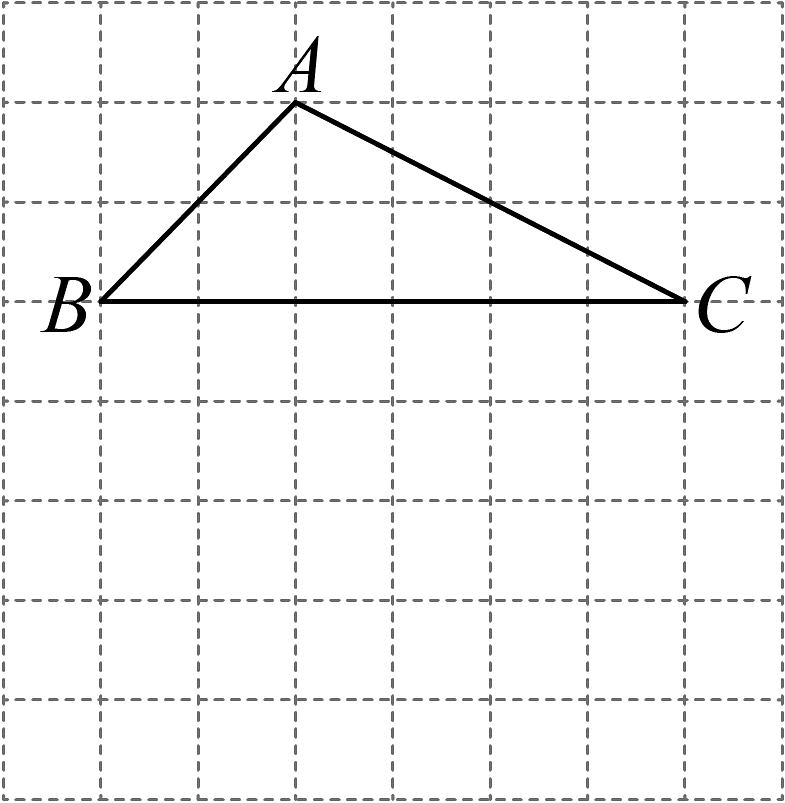 (1)、仅用一把无刻度直尺画出的外心点O.并用圆规面出外接圆;(2)、仅用一把无刻度直尺画弦 , 使得平分 .
(1)、仅用一把无刻度直尺画出的外心点O.并用圆规面出外接圆;(2)、仅用一把无刻度直尺画弦 , 使得平分 . -
16、如图,已知函数图象经过点 ,
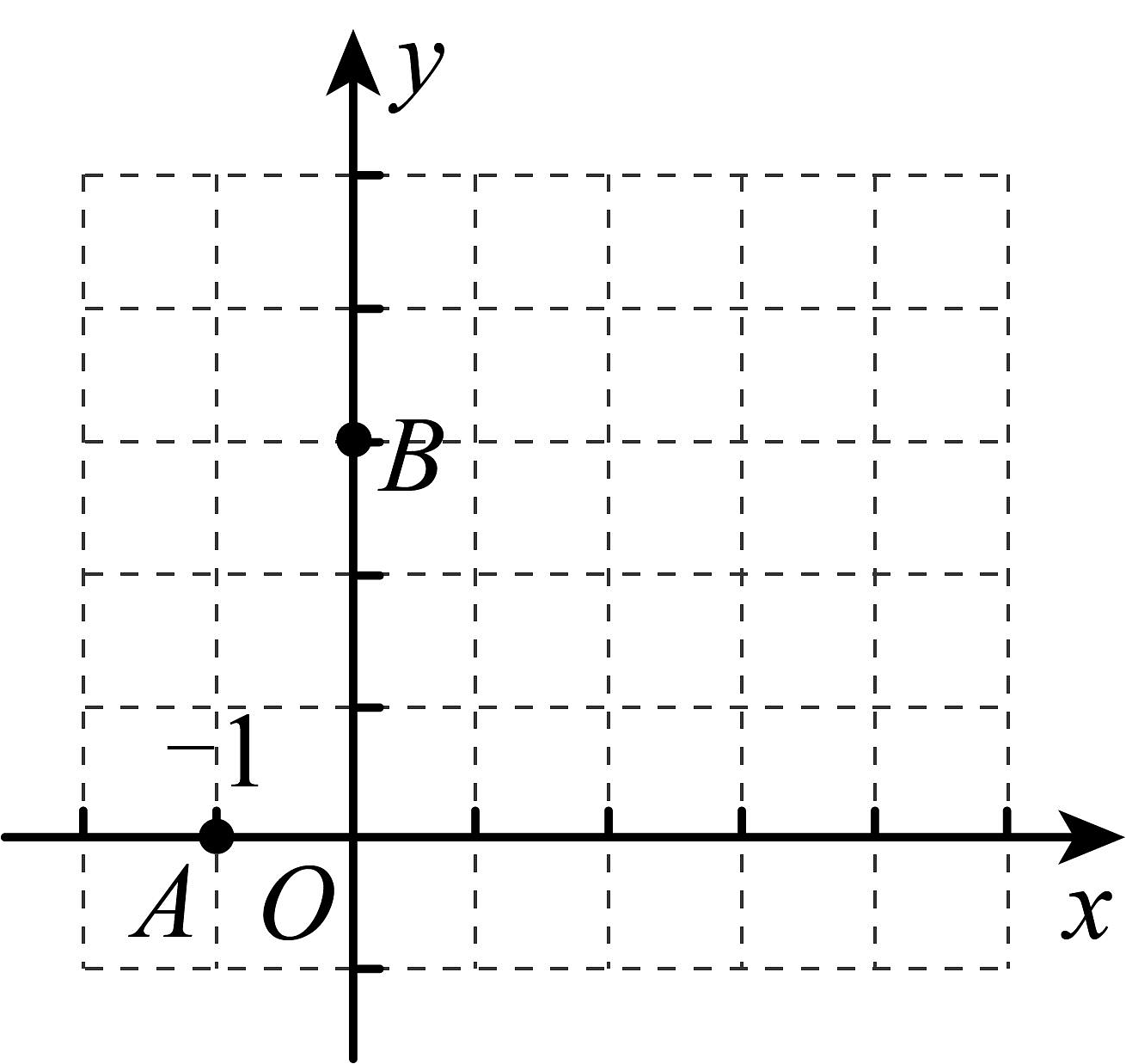 (1)、求b,c的值;(2)、在图中画出这个函数的图象;(不必列表)(3)、观察图像,当时,函数值y的取值范围是 .
(1)、求b,c的值;(2)、在图中画出这个函数的图象;(不必列表)(3)、观察图像,当时,函数值y的取值范围是 . -
17、如图,为的直径,且 , 点C为上半圆的一点,于点E,的角平分线交于点D,弦 , 那么的面积是 .

-
18、二次函数的部分对应值如下表:
x
…
0
1
3
5
…
y
…
7
0
7
…
则二次函数在时, .
-
19、若扇形的圆心角为 , 半径为6,则扇形的面积为 .
-
20、若 , , 为二次函数图象上的三点,则 , , 的大小关系为( )A、 B、 C、 D、