-
1、飞机着陆后滑行的距离y(m)关于滑行时间t(s)的函数表达式为 在飞机着陆滑行中,最后4s 滑行的距离是m.
-
2、若抛物线 满足下列条件:①经过原点;②对称轴在y 轴的左侧,则此抛物线对应的函数表达式为.
-
3、如图所示为二次函数 的部分图象,该函数图象的对称轴是直线x=1,图象与y轴交点的纵坐标是2,有下列结论:①2a+b=0;② 方程 一定有一个根在-2和-1之间;③方程 一定有两个不相等的实数根;④b-a<2.其中,正确结论的个数为( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
4、如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O 在同一水平面.安装师傅调试发现,当喷头高2.5m时,水柱落点距点O2.5m;当喷头高4m时,水柱落点距点O3m.当水柱落点距点O4m时,喷头的高度为( )
 A、5m B、6m C、7m D、8m
A、5m B、6m C、7m D、8m -
5、新定义:若一个点的横纵坐标之和为6,则称这个点为“和谐点”,若二次函数 为常数)在-1<x<3的图象上存在两个“和谐点”,则c 的取值范围是( )A、 B、 C、-1<c<1 D、
-
6、已知二次函数 的图象经过A( , y1),B(3a,y2)两点,则下列判断正确的是( )A、可以找到一个实数a,使得 B、无论实数a 取什么值,都有 C、可以找到一个实数a,使得 D、无论实数a 取什么值,都有
-
7、已知抛物线 上三个点的坐标分别为A(x1 , y1),B(x2 , y2),C(1,y3),若 则y1 , y2 , y3 的大小关系为( )A、 B、 C、 D、
-
8、利用一段长度为8m的旧直墙MN 与长为32m的篱笆围成如图所示的外形为矩形的花圃,则围成的花圃的最大面积是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9、 对于二次函数y=2(x+1)(x-3),下列说法中,正确的是( )A、图象过点(0,-3) B、图象与x 轴的交点坐标为(1,0),(-3,0) C、此函数有最小值为-6 D、当x<1时,y随x 的增大而减小
-
10、抛物线 向左平移3个单位,再向上平移2个单位,所得图象对应的函数表达式为 则b,c 的值为( )A、-8,9 B、-16,29 C、16,33 D、16,29
-
11、在同一平面直角坐标系中,一次函数 与二次函数 的图象可能是 ( )A、
 B、
B、 C、
C、 D、
D、
-
12、下列函数中,不是二次函数的为( )A、 B、 C、 D、
-
13、定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的“遥望角”.
 (1)、 如图①, 是 中 的“遥望角”,若 , 请用含α的代数式表示(2)、 如图②,四边形ABCD 内接于(⊙O, 四边形 ABCD 的外角平分线DF交⊙O于点F,连结BF并延长,交CD 的延长线于点 E,连结AC.求证:是中的“遥望角”.
(1)、 如图①, 是 中 的“遥望角”,若 , 请用含α的代数式表示(2)、 如图②,四边形ABCD 内接于(⊙O, 四边形 ABCD 的外角平分线DF交⊙O于点F,连结BF并延长,交CD 的延长线于点 E,连结AC.求证:是中的“遥望角”. -
14、如图,在正方形ABCD中,AD=2,E 是AB 的中点,将 绕点B 按逆时针方向旋转后,点E落在CB的延长线上的点F处,点C落在点A处.再将线段AF绕点F按顺时针方向旋转90°,得到线段FG,连结EF,CG.
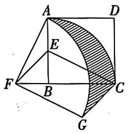 (1)、求证:EF∥CG.(2)、求点C,A在旋转过程中形成的与线段CG所围成的阴影部分的面积.
(1)、求证:EF∥CG.(2)、求点C,A在旋转过程中形成的与线段CG所围成的阴影部分的面积. -
15、如图,AB 是⊙O 的直径,弦( 于点E,G为上一动点,CG 与AB 的延长线交于点 F,连结OD,DG,BG.
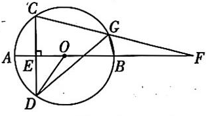 (1)、比较大小: (填“>”“<”或“=”).(2)、 求证:GB平分(3)、在点G运动的过程中,当(GD=GF时, , 求⊙O的半径.
(1)、比较大小: (填“>”“<”或“=”).(2)、 求证:GB平分(3)、在点G运动的过程中,当(GD=GF时, , 求⊙O的半径. -
16、如图,图①、图②、图③、…、图@分别是⊙O的内接正三角形ABC、正四边形ABCD、正五边形ABCDE、…、正n 边形ABCD…,点M,N分别从点B,C 开始以相同的速度在⊙O上沿逆时针方向运动,AM 交BN 于点P.
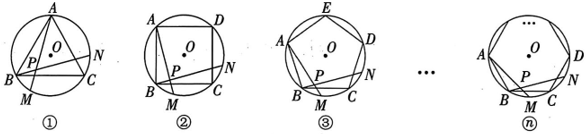 (1)、 求图①中 的度数.(2)、 图②中 的度数是 , 图③中 的度数是.(3)、根据前面探索的判断,本题能否推广到一般的正n 边形的情况?若能,写出结论;若不能,请说明理由.
(1)、 求图①中 的度数.(2)、 图②中 的度数是 , 图③中 的度数是.(3)、根据前面探索的判断,本题能否推广到一般的正n 边形的情况?若能,写出结论;若不能,请说明理由. -
17、如图,在⊙O中,AF,BC是⊙O的弦, , 垂足为D,E 是上一点,且BE=CF.
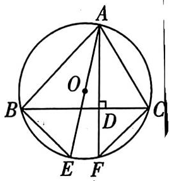 (1)、求证:AE 是⊙O 的直径.(2)、 若 求AC的长.
(1)、求证:AE 是⊙O 的直径.(2)、 若 求AC的长. -
18、如图,四边形ABCD 是⊙O 的内接四边形,DB 平分∠ADC,连结OC,OC⊥BD.
 (1)、 求证:AB=CD.(2)、 若 求 的度数.
(1)、 求证:AB=CD.(2)、 若 求 的度数. -
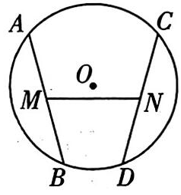
19、 如图,在⊙O中,M,N分别为弦AB,CD 的中点,AB=CD,AB 不平行于CD.
求证:
-
20、在方格纸上建立如图所示的平面直角坐标系,小正方形的边长均为1,的三个顶点都在格点上.
 (1)、 将 绕点B 按顺时针方向旋转,得到 (旋转角小于 , 使得点 落在x轴正半轴上,画出(2)、在(1)的条件下,求线段AB 所扫过的面积.
(1)、 将 绕点B 按顺时针方向旋转,得到 (旋转角小于 , 使得点 落在x轴正半轴上,画出(2)、在(1)的条件下,求线段AB 所扫过的面积.