-
1、临近期末,班级想给优秀的学生准备奖品,奖品分为甲套餐与乙套餐,已知购买个甲套餐比购买个乙套装少用元,用元购买甲套餐和用元购买乙套餐的个数相同.(1)、求这两种套餐的单价分别为多少元;(2)、班级计划用元经费购进甲套餐与乙套餐两种奖品,要求每种套餐至少购进种且刚好用完经费,请你设计进货方案.
-
2、如图,已知 , .
 (1)、求证:(2)、若 , , 求的度数.
(1)、求证:(2)、若 , , 求的度数. -
3、为了解某区七年级男生的身体素质情况,随机抽取了名男生进行短跑测试,将测试成绩(精确到秒)绘制成如图所示的频数表和未完成的频数直方图(每组不含前一个边界值,含后一个边界值).
名男生短跑成绩的频数表
组别(秒)
频数
频率
合计
名男生短跑成绩的频数直方图

根据表中提供的信息解答下列问题:
(1)、频数表中, , , .(2)、把频数直方图补充完整.(3)、若该区七年级共有名男生,请估计短跑成绩小于或等于秒的人数. -
4、先化简 , 然后在2,3,4中选择一个合适的值作为x并代入求值.
-
5、(1)、化简:;(2)、解方程组: .
-
6、计算:(1)、(2)、
-
7、已知 , 是二元一次方程组的解,则的值为 .
-
8、若分式 的值为0,则x= .
-
9、因式分解: =.
-
10、 已知关于x,y的方程组 , 甲同学看错了字母a解得;乙同学看错了字母b解得 , 则该方程组的解为( )A、 B、 C、 D、
-
11、绿色出行,健康出行,你我同行.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图,其中、都与地面平行,与平行,若 , 则的度数为( )
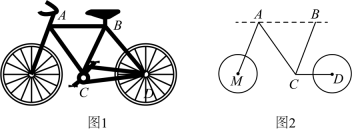 A、 B、 C、 D、
A、 B、 C、 D、 -
12、不改变分式的值,把它的分子与分母中的系数化为整数,下列式子正确的是( )A、 B、 C、 D、
-
13、下列变形是因式分解的是( )A、 B、 C、 D、
-
14、某款风味酸牛奶的营养成分中,碳水化合物含量是蛋白质的4倍,碳水化合物、蛋白质与脂肪的含量共37g.设蛋白质、脂肪的含量分别为(g),(g),可列出方程( )A、 B、 C、 D、
-
15、下列运算正确的是( )A、 B、 C、 D、
-
16、要使分式有意义,的取值应满足( )A、 B、 C、 D、
-
17、如图1,在矩形中, , 点是边上一个动点,点在射线上, . 线段的垂直平分线分别交直线于点、、、 .
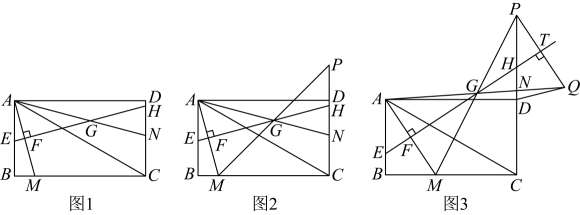 (1)、直接写出°,;(2)、当时,求的值;(3)、如图2,连接并延长交直线于点 .
(1)、直接写出°,;(2)、当时,求的值;(3)、如图2,连接并延长交直线于点 .①求证:;
②如图3,过点作直线的垂线,分别交直线于点 , 连接 , 求线段的最小值.
-
18、定义:在平面直角坐标系中,到两个坐标轴的距离都小于或等于的点叫“阶近轴点”,所有的“阶近轴点”组成的图形记为图形 . 如图所示,所有的“1阶近轴点”组成的图形是以坐标原点为中心,2为边长的正方形区域.
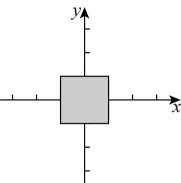 (1)、下列函数图象上存在“1阶近轴点”的是;
(1)、下列函数图象上存在“1阶近轴点”的是;①;②;③ .
(2)、若一次函数的图像上存在“3阶近轴点”,求实数的取值范围;(3)、特别地,当点在图形上,且横坐标是纵坐标的倍时,称点是图形的“阶完美点”,若二次函数的图像上有且只有一个“2阶完美点”,求实数的取值范围. -
19、甲、乙两人从同一地点出发沿同一路线匀速步行前往处参加活动.甲比乙早出发 , 两人途中均未休息,先到达处的人在原地休息等待,直到另一人到达处.两人之间的路程与甲行走的时间的函数图象如图所示.
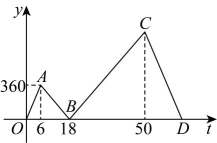 (1)、乙步行的速度为之间的路程为;(2)、当时,求关于的函数表达式;(3)、甲出发多长时间时,两人之间的路程为 .
(1)、乙步行的速度为之间的路程为;(2)、当时,求关于的函数表达式;(3)、甲出发多长时间时,两人之间的路程为 . -
20、如图,点在上,点在外,线段与交于点 , 过点作的切线交直线于点 , 且 .
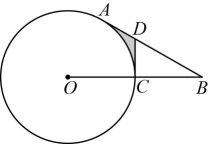 (1)、判断直线与的位置关系,并说明理由;(2)、若 , , 求图中阴影部分的面积.
(1)、判断直线与的位置关系,并说明理由;(2)、若 , , 求图中阴影部分的面积.