-
1、已知线段a=2,b=8,则a , b的比例中项线段是 .
-
2、 设二次函数y=a(x-m)(x-m-2)(a , m是常数,a≠0),则下列说法正确的是( )A、当a=1时,函数y的最小值为2 B、当a=-1时,函数y的最大值为2 C、当a=2时,函数y的最小值为-2 D、当a=-2时,函数y的最大值为-2
-
3、如图,在三角形ABC中, , , 将此三角形绕点沿顺时针方向旋转后得到三角形 , 若点恰好落在线段上,、交于点 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、对于抛物线 ,下列说法错误的是( )A、对称轴是直线 B、函数的最大值是3 C、开口向下,顶点坐标(5,3) D、当时,随的增大而增大.
-
5、关于抛物线y=x2+bx-1与x轴的交点有( )A、0个 B、1个 C、2个 D、3个
-
6、小磊和小轩在课外练习中碰到了一个问题,需要对多项式进行因式分解.小磊认为该整式一定有一个因式 , 小轩认为必有因式是 , 两人找到老师寻求帮助.老师提供了一个方法:因式分解是整式乘法的逆运算.若整式A能被整式B整除,则B必为A的一个因式.老师给出了演算方法:
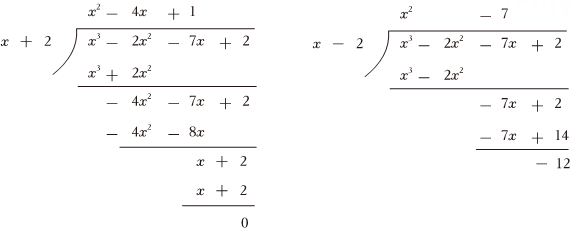 (1)、观察老师的演算后,你认为同学的想法是对的;(2)、已知多项式的其中一个因式为 , 请试着根据老师的方法列出演算过程,并将多项式进行因式分解;(3)、若多项式能因式分解成与另一个完全平方式,求与的值.
(1)、观察老师的演算后,你认为同学的想法是对的;(2)、已知多项式的其中一个因式为 , 请试着根据老师的方法列出演算过程,并将多项式进行因式分解;(3)、若多项式能因式分解成与另一个完全平方式,求与的值. -
7、临近期末,班级想给优秀的学生准备奖品,奖品分为甲套餐与乙套餐,已知购买个甲套餐比购买个乙套装少用元,用元购买甲套餐和用元购买乙套餐的个数相同.(1)、求这两种套餐的单价分别为多少元;(2)、班级计划用元经费购进甲套餐与乙套餐两种奖品,要求每种套餐至少购进种且刚好用完经费,请你设计进货方案.
-
8、如图,已知 , .
 (1)、求证:(2)、若 , , 求的度数.
(1)、求证:(2)、若 , , 求的度数. -
9、为了解某区七年级男生的身体素质情况,随机抽取了名男生进行短跑测试,将测试成绩(精确到秒)绘制成如图所示的频数表和未完成的频数直方图(每组不含前一个边界值,含后一个边界值).
名男生短跑成绩的频数表
组别(秒)
频数
频率
合计
名男生短跑成绩的频数直方图

根据表中提供的信息解答下列问题:
(1)、频数表中, , , .(2)、把频数直方图补充完整.(3)、若该区七年级共有名男生,请估计短跑成绩小于或等于秒的人数. -
10、先化简 , 然后在2,3,4中选择一个合适的值作为x并代入求值.
-
11、(1)、化简:;(2)、解方程组: .
-
12、计算:(1)、(2)、
-
13、已知 , 是二元一次方程组的解,则的值为 .
-
14、若分式 的值为0,则x= .
-
15、因式分解: =.
-
16、 已知关于x,y的方程组 , 甲同学看错了字母a解得;乙同学看错了字母b解得 , 则该方程组的解为( )A、 B、 C、 D、
-
17、绿色出行,健康出行,你我同行.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图,其中、都与地面平行,与平行,若 , 则的度数为( )
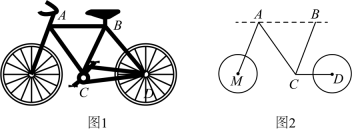 A、 B、 C、 D、
A、 B、 C、 D、 -
18、不改变分式的值,把它的分子与分母中的系数化为整数,下列式子正确的是( )A、 B、 C、 D、
-
19、下列变形是因式分解的是( )A、 B、 C、 D、
-
20、某款风味酸牛奶的营养成分中,碳水化合物含量是蛋白质的4倍,碳水化合物、蛋白质与脂肪的含量共37g.设蛋白质、脂肪的含量分别为(g),(g),可列出方程( )A、 B、 C、 D、