-
1、关于点P(-1,3)和点 Q(-1,5)的说法正确的是( )A、关于直线x=4对称 B、关于直线x=2对称 C、关于直线y=4对称 D、关于直线y=2对称
-
2、若点 M(3a+b,3)和点N(-2,a-2b)关于x轴对称,则a与b的值分别是( )A、2,1 B、1,2 C、1,-1 D、-1,1
-
3、如图,飞机在空中展示的队形是轴对称图形.以飞机 B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机 E 的坐标为(40,a),则飞机D 的坐标为( )
 A、(40,-a) B、(-40,a) C、(-40,-a) D、(a,-40)
A、(40,-a) B、(-40,a) C、(-40,-a) D、(a,-40) -
4、小聪家购买了一辆新能源汽车,该汽车的基本配置为电池容量为60千瓦时,支持快速充电功能,快速充电功率为180千瓦.有关充电小常识如下表所示.
新能源汽车充电小常识:
1.新能源汽车充电有个简单的公式:
充电量(千瓦时)=充电功率(千瓦)×充电时间(时)
2.电动汽车电池剩余20%电量时,提示充电状态,此时电量灯显示为黄色
已知该新能源汽车在满电状态下行驶过程中仪表盘已行驶里程y(千米)与显示电量x(%)的部分数据如下表:(不考虑续航缩水问题)
已行驶里程y(千米)
0
200
300
350
显示电量x(%)
100
60
40
30
 (1)、在直角坐标系中,通过描点画图判断y与x之间的函数关系,并求出该函数表达式.(2)、请问该汽车在满电状态下行驶多少千米时,电量灯开始显示为黄色?(3)、小聪的爸爸驾驶该新能源汽车在满电的状态下出发,前往600千米处的目的地,行驶240千米后,在途中的服务区充电,一次性充电若干时长后继续行驶,到达目的地时仪表盘显示电量为10%,求该汽车在服务区充电的时长.
(1)、在直角坐标系中,通过描点画图判断y与x之间的函数关系,并求出该函数表达式.(2)、请问该汽车在满电状态下行驶多少千米时,电量灯开始显示为黄色?(3)、小聪的爸爸驾驶该新能源汽车在满电的状态下出发,前往600千米处的目的地,行驶240千米后,在途中的服务区充电,一次性充电若干时长后继续行驶,到达目的地时仪表盘显示电量为10%,求该汽车在服务区充电的时长. -
5、已知甲、乙两个仓库分别有物资800 吨和1200 吨,现要把这些物资全部运往A,B 两地,A 地需要物资1300 吨,B地需要物资700吨,从甲、乙两仓库把物资运往A,B两地的运费单价如下表:
A地(元/吨)
B地(元/吨)
甲仓库
12
15
乙仓库
10
18
(1)、设甲仓库运往A 地 x吨物资,直接写出总运费y(元)关于x(吨)的函数表达式(不需要写出自变量的取值范围);(2)、当甲仓库运往A 地多少吨物资时,总运费最少?总运费最少是多少?(3)、若甲仓库运往 A 地的运费下降了 a 元/吨后(2≤a≤6且a为常数),最少的总运费为23 100元,求a 的值. -
6、李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温y(℃)与加热时间x(s)之间近似满足一次函数关系,根据记录的数据,画函数图象如下:
 (1)、加热前水温是℃.(2)、求乙壶中水温y关于加热时间x的函数表达式.(3)、当甲壶中水温刚达到80 ℃时,乙壶中水温是℃.
(1)、加热前水温是℃.(2)、求乙壶中水温y关于加热时间x的函数表达式.(3)、当甲壶中水温刚达到80 ℃时,乙壶中水温是℃. -
7、如图(1),在正方形ABCD 的边 BC上有一点 E,连结AE.点P 从正方形的顶点 A 出发,沿A→D→C 的方向以 1 cm/s 的速度匀速运动到点 C.图(2)是点 P 运动时,△APE 的面积y(cm2)随时间x(s)变化的函数图象,当x=7时,y的值为.

-
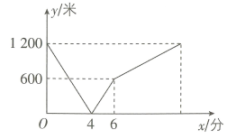
8、A、B两地在一条笔直的公路上,甲从 A 地出发前往B 地,乙从 B 地出发前往 A 地,两人同时出发,甲到达 B 地后停止,乙继续前进到达A地.如图表示两人之间的距离y(米)与乙出发的时间x(分)间的函数关系,则下列结论中:①A、B 两地的距离是 1 200米;②两人出发4分相遇;③甲的速度是 100 米/分;④乙出发12分到达 A 地,正确的有.(填序号)
-
9、某工作室制作工艺品并出售,当工艺品的数量在60个以内时,该工作室制作的工艺品能全部售完.如图所示,线段AB,OC分别表示该工作室每天的制作成本y1(元),收入y2(元)与销售量x(个)之间的函数关系.若该工作室某一天既不盈利也不亏损,则这天生产工艺品的个数是.

-
10、张师傅驾车从甲地到乙地,两地相距500 千米,汽车出发前油箱有油25升,途中加油若干升,加油时间忽略不计.加油前、后汽车都以 100 千米/时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(时)之间的关系如图所示.有下列说法:①加油前油箱中剩余油量y(升)与行驶时间t(时)的函数关系式是y=-8t+25;②途中加油21升;③汽车加油后还可行驶4小时;④汽车到达乙地时油箱中剩余油量为 6 升.其中正确的是( )
 A、①② B、①②③ C、①②④ D、①③④
A、①② B、①②③ C、①②④ D、①③④ -
11、某地区一家供电公司为使居民节约用电,采用分段计费的方法来计算电费,月用电量x(千瓦时)与相应电费y(元)之间的函数图象如图所示.
 (1)、当月用电量为50千瓦时时,应交电费多少元?(2)、当x>100时,求y与x之间的函数关系式.(3)、当月用电量为150千瓦时时,应交电费多少元?
(1)、当月用电量为50千瓦时时,应交电费多少元?(2)、当x>100时,求y与x之间的函数关系式.(3)、当月用电量为150千瓦时时,应交电费多少元? -
12、在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用的时间t(秒)之间的函数图象分别为图中的线段 OA 和折线O-B-C-D,则下列说法正确的是( )
 A、甲的速度随着时间的增大而增大 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时,两人相遇 D、在起跑后第50秒时,乙在甲的前面
A、甲的速度随着时间的增大而增大 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时,两人相遇 D、在起跑后第50秒时,乙在甲的前面 -
13、秤是我国传统的计重工具,秤的应用方便了人们的生活.如图,称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米),秤钩所挂物体的质量为y(千克),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.

x(厘米)
1
2
4
7
11
12
y(千克)
0.75
1.00
1.50
2.75
3.25
3.50
(1)、在上表x,y的数据中,发现有一对数据记录错误.通过描点作图,观察判断哪一对数据是错误的.(2)、当秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物体的质量是多少? -
14、生物活动小组的同学们观察某植物的生长情况,得到该植物的高度y(cm)与观察时间x(天)的关系,画出如图所示的函数图象(CD∥x 轴),则该植物最高长到 cm.

-
15、某种储蓄的月利率为0.2%,如果存入2000元,不计利息税和复利,则本利和y(元)与所存月数x之间的函数关系式是 , 10个月时本利和为元.
-
16、已知一次函数 (a≠0)和 当x≤1时,函数y2的图象在函数y1的图象上方,则a 的取值范围为.
-
17、平面直角坐标系xOy 中,已知A(3,0),B(0,3).直线y= kx+b(k,b为常数,且k>0)经过点(1,0),并把△AOB分成两部分,其中靠近原点部分的面积为 , 则k的值为.
-
18、若正比例函数y=kx(k是常数,k≠0)的图象经过第三、第一象限,则k的值可以是(写出一个即可).
-
19、将常温中的温度计插入一杯60℃的热水(恒温)中,温度计的读数y(℃)与时间x(min)的关系用图象可近似表示为( )A、
 B、
B、 C、
C、 D、
D、
-
20、计算:(1)、(2)、