-
1、对于命题“若a2>b2 , 则a>b”,下面四组关于a , b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=-3,b=2 C、a=3,b=-1 D、a=-1,b=3
-
2、龙门石窟是中国石刻艺术宝库之一,位于洛阳市南郊伊河两岸的龙门山与香山上.为更好地提振文旅消费,该地管理部门推出了针对学生的门票优惠政策.
优惠方案一:每位学生在原价元的基础上全部八折收费.
优惠方案二:若学生人数不超过 , 每位学生在原价元的基础上全部按九折收费;若学生人数超过 , 其中名学生按照原价收费,剩余学生按五折收费.
(1)、分别写出这两个优惠方案实际收取的费用(单位:元)与参观的学生人数之间的函数解析式.(2)、当学生人数超过时,试讨论选择哪种优惠方案较合算. -
3、计算:(1)、(2)、
-
4、如果直线l是由直线向下平移得到,且直线l过点 , 那么直线l的函数表达式为 .
-
5、如图,在中, , , 分别以为一边向外部作正方形,它们的面积分别为、 , 则的值为 .

-
6、点是直线上的两点,则 (填或或)
-
7、在平面直角坐标系中,直线l的解析式为 , 点P的坐标为 , 则点P到直线l的最短距离为 .
-
8、如图,在中, , , , 点是边的中点,点是边上一点,将沿直线折叠,得到 , 连接 , . 若四边形是菱形,则的长为( ).
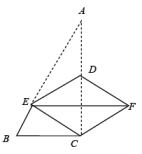 A、1 B、 C、2 D、
A、1 B、 C、2 D、 -
9、1995年,希腊为纪念毕达哥拉斯学派发行了如图1所示的邮票,图案中间的直角三角形由三个正方形顶点相连构成.图2是小华模仿这个图形结构所画的图,则图2中三个正方形的面积可能取值为( )
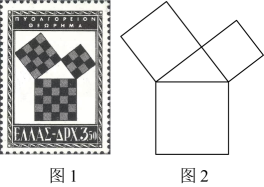 A、2,3,4 B、5,6,11 C、6,8,10 D、7,12,14
A、2,3,4 B、5,6,11 C、6,8,10 D、7,12,14 -
10、如图,已知四边形是平行四边形, , , , 点是上一动点,为的中点,连接 , , 当时,点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、某女子体操队5名队员的身高分别为 , 某男子体操队5名队员的身高分别为 , 则关于这两个队的队员身高,下列描述正确的是( )A、平均数相同 B、中位数相同 C、众数相同 D、方差相同
-
12、已知正比例函数 , 且y的值随x的增大而减小,如果 , 那么和在同一个直角坐标系中的大致图象为( )A、
 B、
B、 C、
C、 D、
D、
-
13、如图,已知矩形的对角线的长为 , 连接矩形各边中点E、F、G、H得四边形 , 则四边形的周长为( ) .
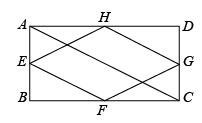 A、10 B、20 C、30 D、40
A、10 B、20 C、30 D、40 -
14、已知:如图,
 (1)、求证:;(2)、若平分平分 , 且 , 求的度数.
(1)、求证:;(2)、若平分平分 , 且 , 求的度数. -
15、为了解七年级学生的计算能力,学校随机抽取了m位学生进行数学计算题测试.王老师将成绩进行统计后分为“优秀”“良好”“一般”“较差”“很差”五个等级,并将收集整理后的数据绘制成如下两幅不完整的统计图.
 (1)、此次调查方式属于;(填“普查”或“抽样调查”)(2)、m= , 扇形统计图中表示“较差”的扇形的圆心角度数为 .(3)、补全条形统计图;(4)、若该校七年级有2400人,估计七年级得“优秀”的学生人数.
(1)、此次调查方式属于;(填“普查”或“抽样调查”)(2)、m= , 扇形统计图中表示“较差”的扇形的圆心角度数为 .(3)、补全条形统计图;(4)、若该校七年级有2400人,估计七年级得“优秀”的学生人数. -
16、在平面直角坐标系中,已知点M的坐标为 , 将点M到x轴的距离记作 , 到y轴的距离记作 .(1)、若 , 求的值;(2)、若点M在第二象限,且(m为常数),求m的值.
-
17、计算:(1)、;(2)、;(3)、解不等式组: , 并写出所有整数解.
-
18、根据光的反射定律,入射光线和平面镜的夹角等于反射光线和平面镜的夹角.如图,笔直的墙面上点的灯泡发出的一束光线照在平面镜上的点, , 反射光线恰好和墙面平行,若 , 则的度数为 .

-
19、x与2的差是正数,用不等式表示为 .
-
20、若是关于、的二元一次方程,则的值为 .