-
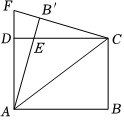
1、如图,在ABCD为矩形中,AC为对角线,将△ABC沿AC翻折,点B的对应点为点B'.AB'与CD相交于点E , 延长CB'与AD相交于点F , 已知AB=4,BC=3,则EC的长为;△ACF的面积为.
-
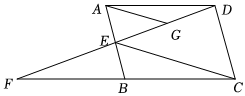
2、如图,在平行四边形ABCD中,点E是AB上一点, , 连接DE并延长交CB的延长线于点F.连接CE , 过点A作AG∥EC交DE于点G , 若AG=10,则CE的长为.
-
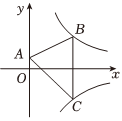
3、如图,点A是y轴上一点,点B , C分别在反比例函数y=(a>0,x>0)和y=(b<0,x>0)的图象上,且BC∥y轴,若△ABC的面积为6,则a-b的值为.
-
4、如图,在△ABC中,AB=AC , ∠A=36°,AB的垂直平分线交AC于点D , 交AB于点E , 则∠CBD= 度.

-
5、一元二次方程3x(x-1)=x-1的解是.
-
6、若3x=5y(y≠0),则的值为.
-
7、如图,在△ABC中,AB=AC , 点D为边AC上中点,点E在线段BC的延长线上,且BD=DE.若CE=3,则BC的长为( )
 A、4 B、5 C、6 D、9
A、4 B、5 C、6 D、9 -
8、已知函数的图象上有三点A(x1 , y1),B(x2 , y2),C(x3 , y3),已知x1<x2<0<x3 , 则下列选项中正确的是( )A、y3<y1<0<y2 B、y2<0<y1<y3 C、y3<0<y1<y2 D、y1<y2<0<y3
-
9、为方便游客观光游览,不少景区预增购一批“游览观光车”.某企业抓住机遇投资15万元购买并投放一批A型“游览观光车”,因需求量增加,计划继续投放B型观光车,B型观光车的投放数量与A型观光车的投放数量相同,投资总费用减少10%,其中B型观光车的单价比A型观光车的单价少30元,则A型观光车的单价是多少元?设A型观光车的单价为x元,根据题意列方程正确的是( )A、 B、 C、 D、
-
10、已知m=4n-4,则(m-4n)2-3(m-4n)-10的值是( )A、-6 B、6 C、18 D、-38
-
11、计算:的结果为( )A、 B、 C、1 D、-1
-
12、褐马鸡是我国的珍稀鸟类,如图是保护褐马鸡宣传牌上利用网格画出的褐马鸡的示意图.若建立适当的平面直角坐标系,表示嘴部点A的坐标为(-3,2),表示尾部点B的坐标为(2,0),则表示足部点C的坐标为( )
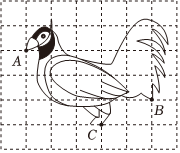 A、(0,1) B、(-1,-1) C、(0,-2) D、(0,-1)
A、(0,1) B、(-1,-1) C、(0,-2) D、(0,-1) -
13、某校801班要选拔一名跳绳成绩优异且发挥稳定的学生参加学校的跳绳比赛.如表是四名候选人十次一分钟跳绳测试成绩的平均数和方差,则应该选择( )号候选人参加比赛.
候选人序号
①
②
③
④
平均数(个)
198
212
205
212
方差(个)
3
3.2
4.5
1.8
A、① B、② C、③ D、④ -
14、下列代数式中,计算正确的是( )A、m3+m3=2m6 B、(mn)6=mn6 C、m2•m3=m6 D、(m3)3=m9
-
15、五边形内角和度数为( )A、270° B、450° C、540° D、900°
-
16、小宁与小波两位同学在学习“平行线”后进行了课后探究:
素材提供:“两块相同直角三角板,两条平行线”.三角板ABC与三角板DEF如图2所示摆放,其中∠ACB=∠DFE=90°,∠BAC=∠FDE=60°,l1∥l2 , 点A , B在直线l1上,点D , E在直线l2上.
动手实践:将三角板沿着直线平移或旋转能形成丰富的图形,也能得到许多有趣的结论.
问题解决:小宁将三角板ABC向右平移.
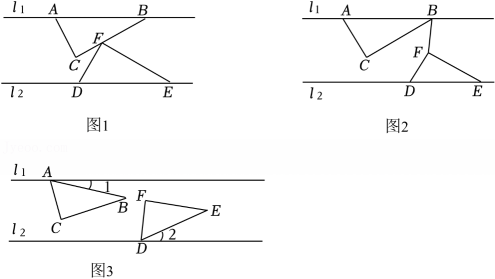 (1)、如图1,当点F落在线段BC上时,求∠BFE的度数.(2)、如图2,在三角板ABC向右平移过程中,连结BF(初始状态E , F , B三点在同一直线上),记∠BFE=α,∠CBF=β.
(1)、如图1,当点F落在线段BC上时,求∠BFE的度数.(2)、如图2,在三角板ABC向右平移过程中,连结BF(初始状态E , F , B三点在同一直线上),记∠BFE=α,∠CBF=β.①当点F在BC右侧时,试探究α与β的数量关系.
②小宁发现,当点F在BC左侧时,α与β的数量关系将发生改变,那么此时α与β的数量关系是 ▲ .
(3)、思维拓展:小宁和小波一起将两块三角板旋转,如图3,小宁将三角板ABC绕点A以每秒1°的速度顺时针旋转,同时小波将三角板DEF绕点D以每秒2°的速度逆时针旋转,设时间为t秒,∠1=t°,∠2=2t°,且0≤t≤60,若边AC与三角板DEF的一条边平行时,请直接写出所有满足条件的t的值. -
17、根据以下素材,探索完成任务.
有A、B两种卡纸,可用来做小旗子,若1张A卡纸和1张B卡纸共能做小旗子8面,2张A卡纸和3张B卡纸共能做小旗子19面.
(1)、求A、B两种卡纸.每张可分别做几面小旗子.(2)、由于艺术节场地布置的需要,某学校打算采购A、B两种卡纸.A卡纸每张4元,B卡纸每张3元,正好赶上商场促销活动:买一张A卡纸,就赠送一张B卡纸.学校计划用这两种卡纸共同做60面小旗子.①制作过程中,若A、B卡纸恰好充分利用,没有余料剩余,则做这些小旗子需要两种卡纸各多少张,并求出最低采购费用.
②由于艺术节实际需要,现须用卡纸再做灯笼42个.已知一张A、B卡纸可分别做灯笼3个和2个.请你结合方案评价表直接写出一种小旗子、小灯笼的制作数量方案(同一张卡纸只能做同一类手工,即不能既做小旗子又做小灯笼,采购费用低于65元).
由A卡纸制作
由B卡纸制作
小旗子(面)
小灯笼(个)
小旗子(面)
小灯笼(个)
方案评价表
方案等级
采购费用
制作中卡纸使用情况
评分
优秀
低于65元
两种卡纸均无余料剩余
3分
良好
低于65元
仅一种卡纸有余料剩余
2分
合格
低于65元
两种卡纸均有余料剩余
1分
-
18、(1)、已知关于x的分式方程 .
①当a=5时,求方程的解.
②若该方程去分母后所得的整式方程的解是增根,求a的值.
(2)、关于x的方程有整数解,求此时整数m的值. -
19、如图,方格纸中每个小正方形的边长都为1,△ABC的顶点均在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C',图中标出了点C的对应点C' .
 (1)、请画出平移后的△A'B'C';(2)、若连接AA' , BB',则这两条线段的关系是 ;(3)、求线段BC扫过的面积.
(1)、请画出平移后的△A'B'C';(2)、若连接AA' , BB',则这两条线段的关系是 ;(3)、求线段BC扫过的面积. -
20、先化简 , 再从0,1,2,中选择一个合适的数代入并求值.