相关试卷
- 广东省汕头市第一中学2024-2025学年高一上学期期中考试物理试题
- 湖南省岳阳市汨罗市第一中学2024-2025学年高二下学期6月期末物理试题
- 浙江省台州市台州十校联考2024-2025学年高一上学期11月期中物理试题
- 广东省清远市2024-2025学年高二上学期期中考试物理试卷
- 广东省惠州市东江高级中学2024-2025学年高一上学期11月期中物理试题
- 广东省惠州市惠州中学2024-2025学年高二上学期11月期中物理试题
- 广东省潮州市高级中学2024-2025学年高二上学期11月期中物理试题
- 广东省肇庆市端州中学2024-2025学年高二上学期期中考试物理试题
- 浙江省强基联盟2024-2025学年高一上学期11月联考物理试题
- 广东省潮州市瓷都中学2024-2025学年高二上学期期中考试物理(选择性)试卷
-
1、如图所示,倾角为α=30°的斜面体固定,下端封闭长为L=150cm的玻璃管,用两段长度均为l=10cm的水银柱将气柱1、2封闭,将玻璃管开口向上静置在斜面上,稳定时气柱1、2的长度分别为l1=40cm,l2=50cm,已知环境温度为t=-23℃,大气压强恒为p0=75cmHg。(以下结果均保留两位有效数字)
(1)仅将玻璃管在竖直平面内沿顺时针方向缓慢转过60°,稳定时空气柱1、2的长度分别为多少?
(2)仅将环境的温度缓慢升高到77℃,通过分析计算是否有水银溢出。

-
2、某实验小组的同学利用实验室提供的实验器材制成了简易欧姆表,电路图如图所示,已知电源的电动势为 , 内阻为 , 电流表的是程为 , 内阻为 , 两滑动变阻器的调节范围足够大。
 (1)、用笔画线代替导线完成电路连接;(2)、该简易欧姆表有两个倍率,开关断开时,欧姆表的倍率为“”,滑动变阻器接入电路的电阻值为 , 在红黑两表笔间接一未知电阻 , 电流表的指针指在处,则;如果开关闭合,欧姆表的倍率为“”,滑动变阻器接入电路的电阻值为(保留三位有效数字),两表笔短接,欧姆调零时,滑动变阻器接入电路的电阻值为;(3)、如果该欧姆表的电池使用时间太长,电动势减小,内阻略微变大,但该欧姆表仍能进行欧姆调零,在测量电阻时,测量值(填“大于”“等于”或“小于”)真实值。
(1)、用笔画线代替导线完成电路连接;(2)、该简易欧姆表有两个倍率,开关断开时,欧姆表的倍率为“”,滑动变阻器接入电路的电阻值为 , 在红黑两表笔间接一未知电阻 , 电流表的指针指在处,则;如果开关闭合,欧姆表的倍率为“”,滑动变阻器接入电路的电阻值为(保留三位有效数字),两表笔短接,欧姆调零时,滑动变阻器接入电路的电阻值为;(3)、如果该欧姆表的电池使用时间太长,电动势减小,内阻略微变大,但该欧姆表仍能进行欧姆调零,在测量电阻时,测量值(填“大于”“等于”或“小于”)真实值。 -
3、某实验小组的同学利用如图甲所示的装置验证机械能守恒定律,在铁架台上固定一角度测量仪,用一长度为L的细线拴接一小球,自然下垂时小球刚好位于光电门处。首先用游标卡尺测量了小球的直径d(d<<L),然后将小球拉离平衡位置一个角度α,使小球由静止释放,记录小球经过光电门时的挡光时间t,多次改变角度α,并记录每次所对应的挡光时间,已知重力加速度为g。
 (1)、用50分度的游标卡尺测量小球的直径时,游标卡尺的读数如图乙所示,该小球的直径d=mm;(2)、实验时(填“需要”或“不需要”)测量小球的质量m;(3)、通过记录的实验数据,以为横轴,欲将图线拟合成一条直线应以(填“”“””或“”)为纵轴,若该过程小球的机械能守恒,则图线的斜率k=(用题中所给字母表示)。
(1)、用50分度的游标卡尺测量小球的直径时,游标卡尺的读数如图乙所示,该小球的直径d=mm;(2)、实验时(填“需要”或“不需要”)测量小球的质量m;(3)、通过记录的实验数据,以为横轴,欲将图线拟合成一条直线应以(填“”“””或“”)为纵轴,若该过程小球的机械能守恒,则图线的斜率k=(用题中所给字母表示)。 -
4、如图所示,半径为的圆弧轨迹沿竖直方向固定,倾角为的光滑斜面与弧形轨道相切于点,点为轨迹的最低点,为圆心,其中 , 质量为可视为质点的物体由点静止释放,经过一段时间运动到点,由于物体与圆弧轨道不同位置之间的动摩擦因数不相同,物体在段做匀速圆周运动。已知点到点的距离为 , 物体在段与段克服摩擦力做的功分别为、 , 重力加速度 , , , 忽略空气阻力。则下列说法正确的是( )
 A、物体从到的过程,合力的冲量等于零 B、 C、物体在、两点重力的瞬时功率之比为 D、物体在、两点对轨道的压力大小之比为
A、物体从到的过程,合力的冲量等于零 B、 C、物体在、两点重力的瞬时功率之比为 D、物体在、两点对轨道的压力大小之比为 -
5、一带正电的物体仅在电场力作用下沿轴正方向运动,物体的动能随位移的变化规律如图所示,已知物体所带的电荷量为 , 坐标原点为电势零点。则下列说法正确的是( )
 A、区域电场方向沿轴正方向 B、与区域电场强度大小之比为 C、处的电势为 D、0与处的电势差为
A、区域电场方向沿轴正方向 B、与区域电场强度大小之比为 C、处的电势为 D、0与处的电势差为 -
6、如图甲所示,一导体棒与导线构成闭合回路,然后用绝缘轻绳悬挂在天花板上,空间存在一圆形磁场区域,导体棒刚好与圆的水平直径重合,磁场方向垂直纸面向外,磁感应强度的大小随时间的变化规律如图乙所示。已知圆形磁场区域的半径为 , 导体棒的质量为、长度为、电阻 , 当时绝缘轻绳的张力刚好为零,忽略导线以及轻绳的重力,重力加速度。则下列说法正确的是( )
 A、内,流过导体棒的电流方向向右 B、 C、流过导体棒的电流为 D、时,轻绳的张力为
A、内,流过导体棒的电流方向向右 B、 C、流过导体棒的电流为 D、时,轻绳的张力为 -
7、6G通信能力将达到5G的10倍以上,5G向6G的发展是从万物互联向“万物智联,数字李生”的一个过程,只要有卫星信号就能够实现6G通讯。假设如图所示的四颗卫星刚好覆盖全球通讯,四颗卫星到地面的高度相等,已知地球的半径为R,同步卫星到地面的高度为地球半径的6倍,公转周期为T,引力常量为G,忽略四颗卫星间的万有引力,下列说法正确的是( )
 A、地球的密度为 B、地球表面的重力加速度为 C、四颗卫星到地球表面的高度为 D、四颗卫星的环绕周期为
A、地球的密度为 B、地球表面的重力加速度为 C、四颗卫星到地球表面的高度为 D、四颗卫星的环绕周期为 -
8、如图甲所示为一列水平向右传播的简谐横波上的两质点a、b,两质点之间的距离为x=3m,a、b两质点的振动图像分别如图乙、丙所示,已知波长。下列说法正确的是( )
 A、该波的波长可能为18m B、该波的波速为1.2m/s C、从t=0时刻起1.5s内,质点a通过的路程为 D、从t=0时刻起1.5s内,质点b通过的路程为
A、该波的波长可能为18m B、该波的波速为1.2m/s C、从t=0时刻起1.5s内,质点a通过的路程为 D、从t=0时刻起1.5s内,质点b通过的路程为 -
9、如图所示,两人用轻绳拴接一重物于点,跨过两侧的定滑轮用外力缓慢地竖直提升重物,已知与竖直方向夹角分别为(变化),左右两侧施加的外力大小分别为 , 两定滑轮处在同一高度。则下列说法正确的是( )
 A、 B、一直减小,也一直减小 C、为定值 D、的合力大于重物的重力
A、 B、一直减小,也一直减小 C、为定值 D、的合力大于重物的重力 -
10、甲、乙两小球在光滑的水平面上沿同一直线相向运动,已知小球甲的质量小于小球乙的质量,两小球碰撞前后的位移随时间的变化规律如图所示。则下列说法正确的是( )
 A、图线A为碰前乙的位移—时间图像 B、图线C为碰后甲的位移—时间图像 C、小球甲、乙的质量之比为1∶2 D、两小球的碰撞为非弹性碰撞
A、图线A为碰前乙的位移—时间图像 B、图线C为碰后甲的位移—时间图像 C、小球甲、乙的质量之比为1∶2 D、两小球的碰撞为非弹性碰撞 -
11、如图所示为某透明介质制成的棱镜截面,该截面由扇形和直角三角形构成,已知 , , 一细光束由平面上的A点斜射入棱镜,细光束在D点刚好发生全反射,已知弧长等于弧长的3倍,光在真空中的速度为。下列说法正确的是( )
 A、该透明介质的折射率为 B、光束在点入射角的正弦值为 C、光线第一次射出棱镜时从边射出 D、光束从点射入到第一次从棱镜中射出的时间为
A、该透明介质的折射率为 B、光束在点入射角的正弦值为 C、光线第一次射出棱镜时从边射出 D、光束从点射入到第一次从棱镜中射出的时间为 -
12、如图甲、乙所示的交流电分别加在两定值电阻R1、R2两端,已知R1=2R2 , 若两图中的横、纵坐标均为已知量,图甲为正弦曲线。则下列说法正确的是( )
 A、甲图中交流电压的有效值为 B、乙图中交流电压的有效值为 C、0~时间内两定值电阻R1、R2上产生的热量之比为1:16 D、0~T时间内两定值电阻R1、R2上产生的热量之比为1:5
A、甲图中交流电压的有效值为 B、乙图中交流电压的有效值为 C、0~时间内两定值电阻R1、R2上产生的热量之比为1:16 D、0~T时间内两定值电阻R1、R2上产生的热量之比为1:5 -
13、大量处在激发态n的氢原子向基态跃迁时能向外辐射三种不同波长的光子,三种光子的波长分别为 , 且有 , 波长为的光能使某种金属发生光电效应现象。则下列说法正确的是( )A、 B、波长为的光一定能使该金属发生光电效应现象 C、 D、跃迁后的氢原子电势能不变
-
14、某实验小组同学利用电磁打点计时器做“探究小车速度随时间变化的规律”的实验。
装置如图甲所示,其中斜面倾角θ可调。

(1)实验过程中,下列实验操作中错误的是。
A.打点计时器应使用交流电源
B.将小车停靠在打点计时器附近,小车尾部与纸带相连
C.实验开始时,先释放小车,再接通打点计时器电源
D.打点结束后,先断开电源,再取下纸带
(2)该小组的同学得到一条清晰的纸带如图乙所示,并在其上依次取A、B、C、D、E、F、G共7个点。已知打点计时器工作电源的频率为f,则打点D时的速度大小为;为减小误差,充分利用数据,计算加速度大小的表达式应为。(用题和图中字母表示)
(3)如果当时电网中交变电流的频率大于f,做实验的同学并不知道,那么由此测量计算出的加速度值比实际值偏(填“大”或“小”)。
-
15、固定的“三叶式”线圈处于垂直纸面向里、磁感应强度为B的匀强磁场中,如图所示,线圈六段圆弧的圆心角均为圆心均在О点,其中小圆弧半径均为r、大圆弧半径均为2r。现有长为2r、电阻R的均匀导体棒OA可绕О点在纸面内匀速转动,从圆弧边缘和圆心用细导线连接足够长的两平行金属导轨PQ、MN,导轨与水平面夹角为α,导轨空间存在垂直导轨平面向上的磁感应强度大小为B的匀强磁场,质量为m的金属棒ab静止在导轨上且垂直导轨。导轨宽度和金属棒ab长度均为L,金属棒与导轨之间的动摩擦因数为(),ab棒电阻也为R其余电阻不计,重力加速度为g。
(1)若OA棒在大圆弧区域以角速度顺时针(俯视)匀速转动,ab棒保持静止,求流过OA棒的电流方向和ab棒两端的电压:
(2)若OA棒以角速度顺时针(俯视)匀速转动一周过程中,ab棒始终保持静止,求此过程通过ab棒的电流的宥效值;
(3)若OA棒在小圆弧区域逆时针(俯视)匀速转动时,要使ab棒与导轨保持相对静止,求OA棒转动的角速度应满足的条件。

-
16、如图所示,竖直面内有一租细均匀的U形玻璃管。初始时,U形管右管上端封有压强p0=76cmHg的理想气体A,左管上端封有长度L1=8cm的理想气体B,左右两侧水银面高度差L2=4cm,此时A、B气体的温度均为T0=288K。
(1)求初始时理想气体B的压强;
(2)保持气体A温度不变,对气体B缓慢加热。求右侧液面上升△h=4cm时气体A的压强和气体B的益度。

-
17、在很多餐馆中,“机器人服务员”(图甲)已替代人工进行配送服务。厨师将餐盘放在机器人的水平托盘上,机器人沿如图乙中的ABCD的路径(同一水平面)把餐盘送到目标餐桌。已知半径为R=4m的圆弧BC与直线路径CF相切。若机器人从第1个餐桌左边位置D点到E点(未画出),以v=1m/s的速率做匀速运动,用时。此后,机器人以最大加速度从E点开始做匀减速直线运动,到F点时速度恰好减为零。用时t2。已知:每个就餐区域宽为 , 配送全程餐盘与托盘无相对滑动,餐盘和托盘间的动摩擦因数为μ=0.1,g取10m/s2 , 求:
(1)机器人匀速率通过BC段时的最大允许速率以及时间;
(2)机器人在此过程中经过的餐桌数量n。

-
18、某同学要探究光敏电阻阻值随光照强度变化的规律,实验电路如图甲所示。



实验器材如下:
A.待测光敏电阻Rx(日光下阻值约几千欧)
B.标准电阻R1(阻值为10Ω)
C.标准电阻R2(阻值为4Ω)
D.灵敏电流计G(量程为300μA,a端电势高于b端电势,电流计向左偏转,b端电势高于a端电势,电流计向右偏转)
E.电阻箱R3(0~9999Ω)
F.滑动变阻器(最大阻值为20Ω,允许通过的最大电流为2A)
G.电源(电动势3.0V,内阻约为0.2Ω)
H.开关,导线若干
(1)、①开关闭合前,滑动变阻器滑片应置于(填“A”或“B”)端。②多次调节滑动变阻器和电阻箱,使电流计指针稳定时指向中央零刻线位置。电阻箱示数如图乙所示,电阻箱接入电路的阻值R3=Ω。
(2)、待测光敏电阻R计算公式为(用R1 , R2 , R3表示)。(3)、该同学找到该光敏电阻的阻值与光照强度的关系图像如图丙所示,则上述实验中光强强度为cd;(4)、若保持电阻箱阻值不变,增大光照强度,则电流计指针(填“向左”或“向右”或“不”)偏转。 -
19、如图所示,质量为m,带电量为+q的点电荷,从原点以初速度射入第一象限内的电磁场区域,在 , (、为已知)区域内有竖直向上的匀强电场,在区域内有垂直纸面向里的匀强磁场B,控制电场强度(E值有多种可能),均可让粒子从NP射入磁场后偏转打到接收器MN上,则( )
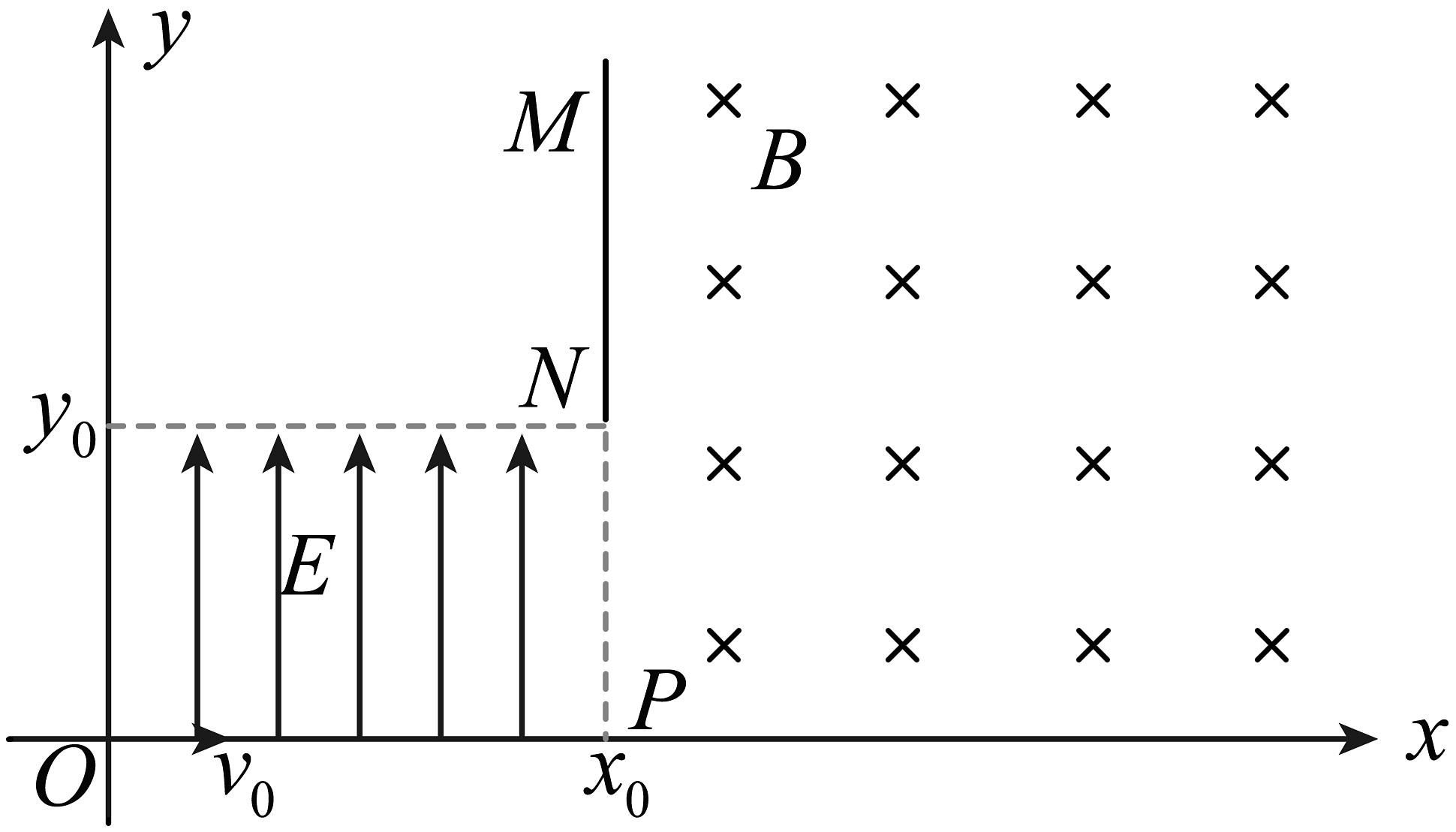 A、粒子从距N点的NP处射入磁场,电场强度满足 B、粒子在磁场中做圆周运动的圆心到MN的距离为 C、粒子在磁场中运动的圆周半径最大值是 D、粒子从О点到MN整个过程的运动时间是(其中的反三角函数)
A、粒子从距N点的NP处射入磁场,电场强度满足 B、粒子在磁场中做圆周运动的圆心到MN的距离为 C、粒子在磁场中运动的圆周半径最大值是 D、粒子从О点到MN整个过程的运动时间是(其中的反三角函数) -
20、如图所示,轻弹簧的一端固定在竖直墙壁上,小球A向左压缩弹簧并锁定,弹簧具有弹性势能 , 带有四分之一光滑圆弧轨道的滑块B静止放在A的右侧,轨道下端与水平面相切,整个装置位于足够大的光滑水平面上。某时刻解锁,小球被弹出后向右运动,经轨道滑上滑块B,已知A、B的质量分别为m、3m,重力加速度为g则下列说法正确的是( )
 A、小球沿B的轨道上升时,A和B组成的系统动量守恒 B、小球A上升到最高点的速度大小为 C、小球可以第二次从水平面滑上B的轨道 D、滑块B的最大动能为
A、小球沿B的轨道上升时,A和B组成的系统动量守恒 B、小球A上升到最高点的速度大小为 C、小球可以第二次从水平面滑上B的轨道 D、滑块B的最大动能为