相关试卷
-
1、定义:已知集合 , , , 则称为“有界恒正不等式”.
(1)当时,判断是否为“有界恒正不等式”;
(2)设为“有界恒正不等式”,求的取值范围.
-
2、已知函数 .(1)、当时,判断函数的单调性并证明;(2)、若不等式成立,求实数x的取值范围.
-
3、某游乐场需要修建一间背面靠围墙的矩形母婴室,地面面积为5平方米,地面费用总价为五千元.现需要对母婴室外墙正面和屋顶进行带有游乐场主题特色的装修,因此外墙正面每平方米造价为1500元,屋顶造价一万元;母婴室外墙侧面普通装修即可,每平方米造价600元;母婴室墙高3米,不计母婴室背面费用.(1)、若游乐场母婴室正面长设为x米,请用x表示该游乐场母婴室的总造价元(2)、如何设计能使得该游乐场母婴室的总造价最低?最低总造价为多少?
-
4、已知函数满足(1)、求的解析式;(2)、求函数在上的值域.
-
5、已知全集 , 集合 , .(1)、当时,求 , ;(2)、若 , 求a的取值范围.
-
6、已知函数的定义域为 , 则函数的定义域为 .
-
7、请写出命题“ , ”的否定: .
-
8、设a>0,b>0,则下列不等式中一定成立的是( )A、a+b+≥2 B、≥ C、≥a+b D、(a+b)≥4
-
9、已知函数 , , 则下列说法中正确的是( )A、是偶函数 B、是奇函数 C、 D、
-
10、下列各组函数中是同一函数的是( )A、与 B、与 C、与 D、与
-
11、已知 , 对于 , 且 , 则称为的“孤立元”.给定集合 , 则的所有子集中,只有一个“孤立元”的集合的个数为( )A、5 B、7 C、13 D、15
-
12、的定义域为 , 满足 , 则的最小值为( )A、 B、 C、 D、
-
13、幂函数的图象经过点 , 则是( )A、偶函数,且在上是减函数 B、偶函数,且在上是增函数 C、奇函数,且在上是减函数 D、非奇非偶函数,且在上是增函数
-
14、方程有两个异号实根的一个充要条件是( )A、 B、 C、 D、
-
15、下列命题为真命题的是( )A、若 , 则 B、集合与集合是相同的集合 C、任意一个三角形,它的内角和大于或等于 D、所有的素数都是奇数
-
16、若 , 则下列命题正确的是 ( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
17、设全集 , , , 则( )A、 B、 C、 D、
-
18、已知两个非零向量 , 在空间任取一点 , 作 , , 则叫做向量与的夹角,记作 . 定义与的“向量积”为:是一个向量,它与向量 , 都垂直,它的模 . 如图,在正四棱锥中, , 且 .
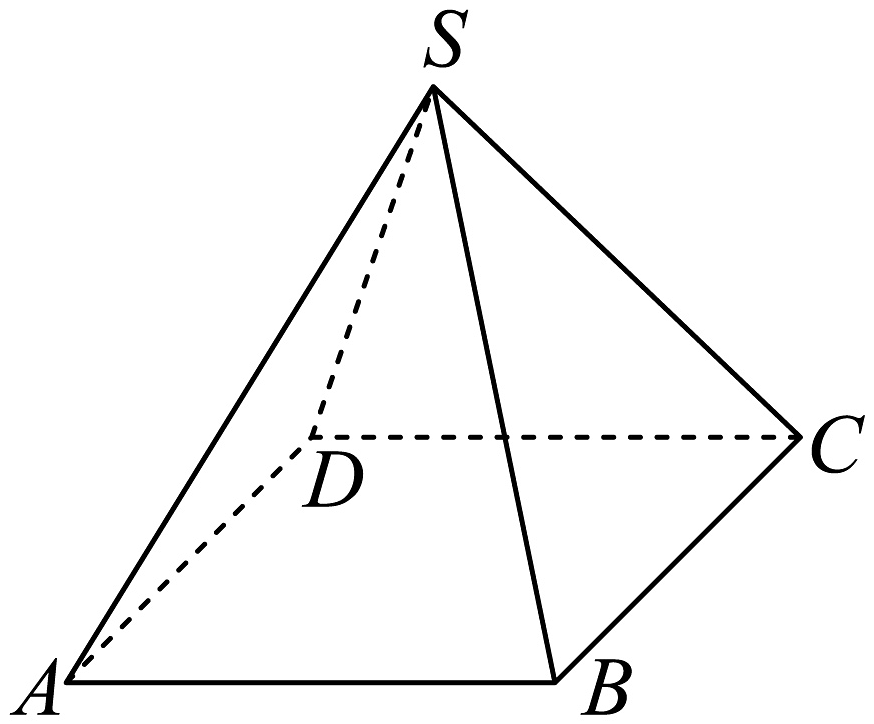 (1)、求正四棱锥的体积;(2)、若为侧棱上的点,且平面 , 求平面与平面夹角的余弦值;(3)、若点是侧棱(包含端点)上的一个动点,当直线与平面所成角最大时,求的值.
(1)、求正四棱锥的体积;(2)、若为侧棱上的点,且平面 , 求平面与平面夹角的余弦值;(3)、若点是侧棱(包含端点)上的一个动点,当直线与平面所成角最大时,求的值. -
19、已知曲线M是平面内到和的距离之和为4的点的轨迹.(1)、求曲线M的方程;(2)、过点作斜率不为0的直线l交曲线M于两点,交直线于点P,过点P作y轴的垂线,垂足为Q,直线AQ交x轴于C点,直线BQ交x轴于D点,求线段CD中点的坐标.
-
20、如图,四棱锥中,侧面为等边三角形且垂直于底面 , , , E是PD的中点.
 (1)、证明:平面;(2)、当点为棱中点时,求直线与平面所成角的正弦值.
(1)、证明:平面;(2)、当点为棱中点时,求直线与平面所成角的正弦值.