相关试卷
-
1、在四棱锥中,底面是平行四边形,点E满足 , 点F满足 , 若四点共面,则.
-
2、直线在两坐标轴上的截距互为相反数,则m的值为.
-
3、已知 , , 是曲线上的任意一点,若的值与无关,则( )A、m的取值范围为 B、n的取值范围为 C、的最大值为7 D、的最小值为
-
4、在四棱锥中, , , , , , 则下列结论正确的有( )A、四边形为正方形 B、四边形的面积为 C、在上的投影向量的坐标为 D、点到平面的距离为
-
5、已知曲线 , 则下列结论正确的有( )A、若 , 则C是焦点在轴上的椭圆 B、若 , 则C是圆 C、若 , 则C是焦点在轴上的椭圆 D、若 , 则C是两条平行于y轴的直线
-
6、在空间直角坐标系中,定义:经过点且一个方向向量为的直线l的方程为 , 经过点且法向量为的平面的方程为.已知在空间直角坐标系中,经过点的直线的方程为 , 经过点的平面的方程为 , 则直线与平面所成角的正弦值为( )A、 B、 C、 D、
-
7、一条光线从点射出,经直线反射后,与圆相切于点M,则光线从P到M经过的路程为( )A、4 B、5 C、 D、
-
8、已知 , , , , , 若从A,B,C,D,E这五个点中任意选择两个点,则这两个点都落在圆外的概率为( )A、 B、 C、 D、
-
9、已知椭圆 , 为坐标原点,直线与椭圆交于两点.若为直角三角形,则的离心率为( )A、 B、 C、 D、
-
10、若圆的圆心到两坐标轴的距离相等,则( )A、 B、1 C、 D、
-
11、已知向量 , , 若 , 则( )A、 B、2 C、 D、1
-
12、已知为随机事件,A与B互斥,B与C互为对立,且 , , 则( )A、0.06 B、0.5 C、0.6 D、0.7
-
13、下列直线中,倾斜角最大的是( )A、 B、 C、 D、
-
14、如图,在四棱锥中,平面 , 且.
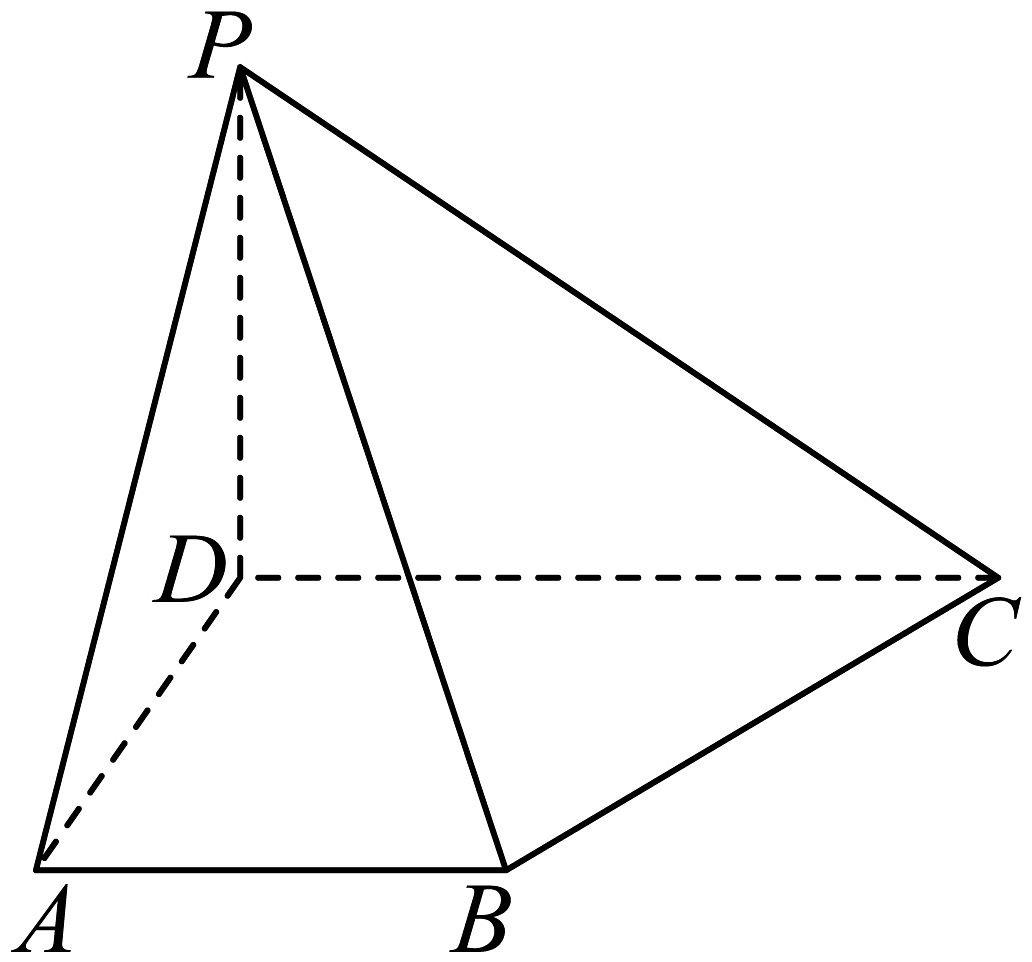 (1)、求证:平面;(2)、求平面与平面夹角的余弦值;(3)、在棱上是否存在点(与不重合),使得与平面所成角的正弦值为?若存在,求的值,若不存在,说明理由.
(1)、求证:平面;(2)、求平面与平面夹角的余弦值;(3)、在棱上是否存在点(与不重合),使得与平面所成角的正弦值为?若存在,求的值,若不存在,说明理由. -
15、2024年奥运会在巴黎举行,中国代表团获得了40枚金牌,27枚银牌,24枚铜牌,共91枚奖牌,取得了境外举办奥运会的最好成绩,运动员的拼搏精神给人们留下了深刻印象.为了增加学生对奥运知识的了解,弘扬奥运精神,某校组织高二年级学生进行了奥运知识能力测试.根据测试成绩,将所得数据按照 , , , , , 分成6组,其频率分布直方图如图所示.
 (1)、求a值和该样本的第75百分位数;(2)、试估计本次奥运知识能力测试成绩的平均分;(3)、该校准备对本次奥运知识能力测试成绩不及格(60分以下)的学生,采用按比例分配的分层随机抽样方法抽出5名同学,再从抽取的这5名同学中随机抽取2名同学进行情况了解,求这2名同学分数在 , 各一人的概率.
(1)、求a值和该样本的第75百分位数;(2)、试估计本次奥运知识能力测试成绩的平均分;(3)、该校准备对本次奥运知识能力测试成绩不及格(60分以下)的学生,采用按比例分配的分层随机抽样方法抽出5名同学,再从抽取的这5名同学中随机抽取2名同学进行情况了解,求这2名同学分数在 , 各一人的概率. -
16、在中,角所对边分别为 , 且.(1)、求角的大小;(2)、若.
(i)求的值;
(ii)求的值.
-
17、已知空间三点 , , .(1)、求向量与的夹角;(2)、若 , 求实数的值.(3)、求的面积.
-
18、在棱长为2的正方体中,E为的中点,以D为原点,所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则点到直线的距离为;点D到平面的距离为 .

-
19、与椭圆有相同的焦点,且过点的椭圆方程为 .
-
20、函数的定义域为.