相关试卷
-
1、已知 , 分别为双曲线C:( , )的左、右焦点,A为双曲线C上的一点,且 , , , 则双曲线C的离心率为( )A、 B、 C、 D、3
-
2、已知圆锥的顶点为P,底面圆心为O,底面半径为2,该圆锥PO侧面展开图的圆心角为 , 则圆锥PO的体积为( )A、 B、 C、 D、
-
3、在中,角的对边分别为 , 若.则角的大小为( )A、 B、 C、 D、
-
4、已知事件 , 是相互独立事件,且 , , 则( )A、 B、 C、 D、
-
5、设复数z满足(是虚数单位),则复数z的虚部为( )A、 B、 C、 D、
-
6、已知集合 , , , 则( )A、 B、 C、 D、
-
7、直线与圆的位置关系是( )A、相切 B、相交 C、相离 D、不确定
-
8、如图,在平面四边形中,为等腰直角三角形,为正三角形, , , 现将沿翻折至 , 形成三棱锥 , 其中为动点.
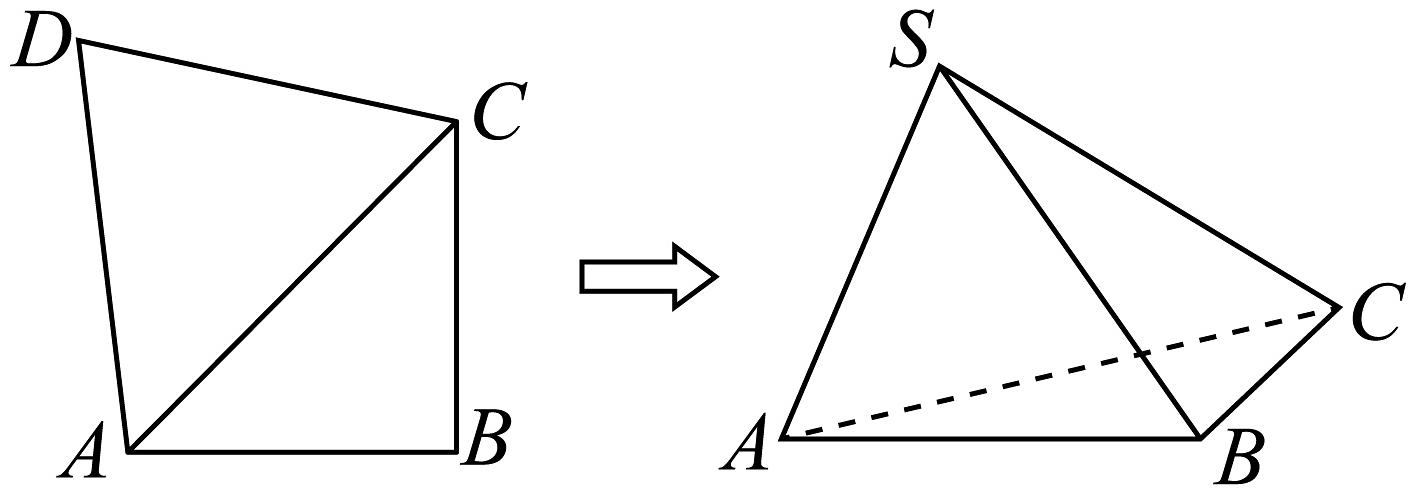 (1)、证明:;(2)、若 , 三棱锥的各个顶点都在球的球面上,求球心到平面的距离;(3)、求平面与平面夹角余弦值的最小值.
(1)、证明:;(2)、若 , 三棱锥的各个顶点都在球的球面上,求球心到平面的距离;(3)、求平面与平面夹角余弦值的最小值. -
9、如图,在边长为的正方形中, , 分别为边 , 上的点,连接 , , , 将沿着折线翻折,使点到达点位置,连接 , 形成三棱锥.
 (1)、若 , 分别为边 , 上的中点, , 求此时三棱锥外接球的表面积;(2)、若 , 是的中点.
(1)、若 , 分别为边 , 上的中点, , 求此时三棱锥外接球的表面积;(2)、若 , 是的中点.(ⅰ)求的大小;
(ⅱ)若正方形边长为 , 当取最小值,取最大值时,求此时直线与平面所成角的正弦值.
-
10、已知函数.(1)、当时,讨论的单调性;(2)、若有两个零点,为的导函数.
(i)求实数的取值范围;
(ii)记较小的一个零点为 , 证明:.
-
11、设抛物线的焦点为 , 过且斜率为的直线与抛物线交于 , 两点,.
(1)求抛物线的方程;
(2)若关于轴的对称点为 , 求证:直线恒过定点,并求出该点的坐标.
-
12、在某地区进行流行病学调查,随机调查了100位患者的年龄并得到如下频率分布直方图(每一组区间均是前闭后开),回答下列问题:
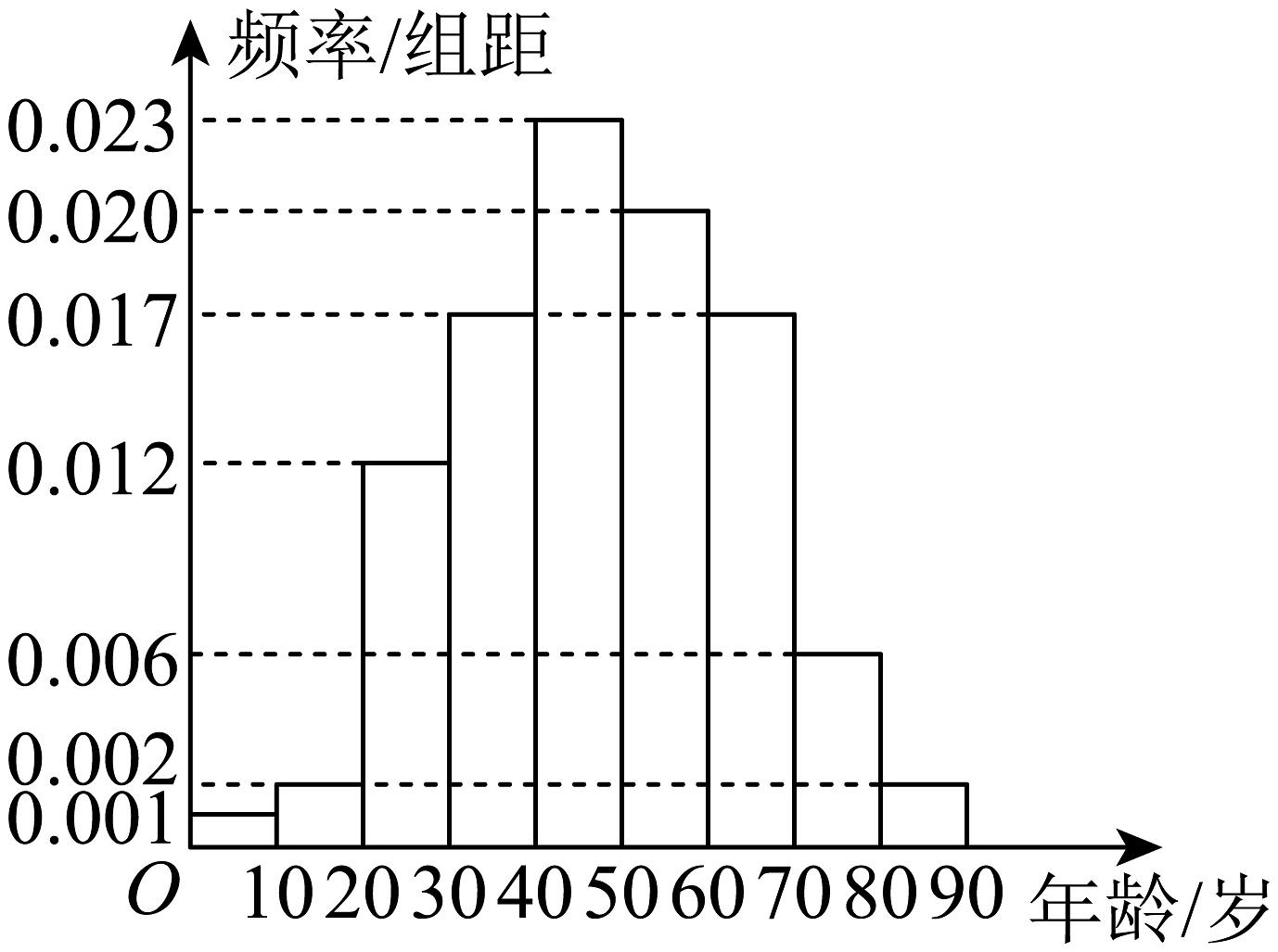 (1)、估计该地区这种疾病患者的平均年龄(同一组中的数据用该组区间的中点值为代表);(2)、估计该地区一位这种疾病患者的年龄位于区间的概率;(3)、已知该地区这种疾病的患病率为 , 该地区年龄位于区间的人口占该地区总人口的.从该地区中任选一人,若此人的年龄位于区间 , 求此人患这种疾病的概率(以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率,精确到0.0001).
(1)、估计该地区这种疾病患者的平均年龄(同一组中的数据用该组区间的中点值为代表);(2)、估计该地区一位这种疾病患者的年龄位于区间的概率;(3)、已知该地区这种疾病的患病率为 , 该地区年龄位于区间的人口占该地区总人口的.从该地区中任选一人,若此人的年龄位于区间 , 求此人患这种疾病的概率(以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率,精确到0.0001). -
13、在数列中, , 点在直线上(1)、求数列的通项公式;(2)、记 , 证明数列的前n项和.
-
14、已知直三棱柱中, , 且.若三棱柱的外接球的表面积是 , 则此三棱柱的体积的最大值是.
-
15、 的展开式的常数项是(用数字作答).
-
16、已知双曲线的渐近线与圆相切, , 为的左、右焦点,动点在的左支上,则( )A、 B、为直角三角形 C、周长的最小值为 D、的最小值为2
-
17、已知正项等比数列的公比为 , 若 , 且 , 则( )A、 B、 C、是数列中的项 D、 , , 成等差数列
-
18、设椭圆的左、右焦点分别为、 , 点在椭圆上,为的平分线与轴的交点.若 , 则( )A、 B、 C、 D、
-
19、某新能源汽车公司生产的电池容量(单位:千瓦时),且 . 若质检部门随机抽检块电池,则恰好有块电池的容量在千瓦时以上的概率为( )A、 B、 C、 D、
-
20、2024年汤姆斯杯暨尤伯杯羽毛球团体锦标赛于4月27日在四川成都开赛.为保证锦标赛顺利进行,组委会需要提前把各项工作安排好.现要把甲、乙、丙、丁四名志愿者安排到七天中服务,若甲去两天,乙去三天,丙和丁各去一天,则不同的安排方法有( )A、140种 B、210种 C、420种 D、840种