相关试卷
-
1、已知函数的定义域为且满足 , 当时,.
(1)判断在上的单调性并加以证明;
(2)若方程有实数根 , 则称为函数的一个不动点,设正数为函数的一个不动点,且 , 求的取值范围.
-
2、给定椭圆 , 称圆心在原点、半径为的圆是椭圆的“卫星圆”,若椭圆的离心率为 , 点在上.
(1)求椭圆的方程和其“卫星圆”方程;
(2)点是椭圆的“卫星圆”上的一个动点,过点作直线、使得 , 与椭圆都只有一个交点,且、分别交其“卫星圆”于点、 , 证明:弦长为定值.
-
3、某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
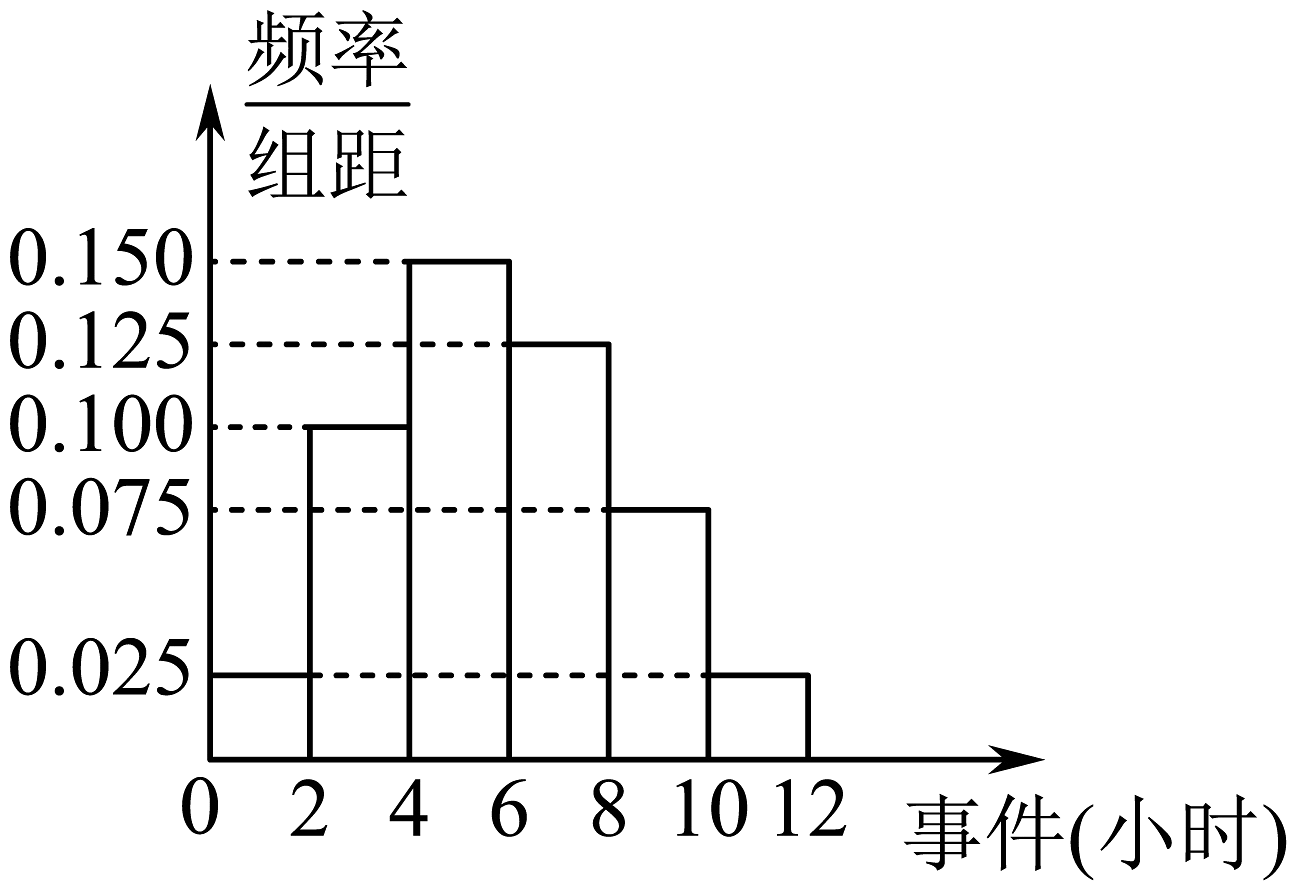 (1)、应收集多少位女生样本数据?(2)、根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: , , , , , . 估计该校学生每周平均体育运动时间超过4个小时的概率.(3)、视样本数据的频率为概率,现从全校取4名学生,记为这四名学生中运动时间超过4小时的人数,求的分布列以及数学期望.
(1)、应收集多少位女生样本数据?(2)、根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: , , , , , . 估计该校学生每周平均体育运动时间超过4个小时的概率.(3)、视样本数据的频率为概率,现从全校取4名学生,记为这四名学生中运动时间超过4小时的人数,求的分布列以及数学期望. -
4、已知函数有两个不同零点 , 且 , 则下列选项正确的是( )A、 B、 C、 D、
-
5、为了迎接2023年五四青年节,厦门一中计划在两个校区各布置一个优秀青年校友的事迹展板,由甲、乙在内的5名学生志愿者协助布置,每人参与且只参与一个展板的布置,每个展板都至少由两人安装,若甲和乙必须安装不同的展板,则不同的分配方案种数为( )A、8 B、10 C、12 D、14
-
6、不透明的盒子里装有除颜色外完全相同的3个黑球、2个白球,其中黑球编号为1,2,3,白球编号为4,5.(1)、现从盒子里随机取出2个小球,记事件“有放回地依次取出时,取到两个白球”,事件“不放回地依次取出时,取出小球编号之和为”,当时,分别求事件的概率;(2)、某班级为活跃班级氛围,组织了玩游戏送书签的活动.该活动由三个游戏组成,每个游戏各玩一次且结果互不影响,连胜两个游戏可以获得一张书签,连胜三个游戏可以获得两张书签.
游戏一:从盒子中随机取出一个球,取到白球时获胜;
游戏二:从盒子中有放回地依次取出2个球,取出两个白球时获胜;
游戏三:从盒子中无放回地依次取出2个球,取出球编号之和为时获胜.
小明同学决定先玩游戏一,当为何值时,接下来先玩游戏三比先玩游戏二获得书签的概率更大?
-
7、某校在2025年高三二轮复习备考中,年级备课组命制了一套与数学新定义有关的专题训练卷(满分100分),并对整个高三年级的学生进行了测试.现从全部高三年级学生的成绩中随机抽取了100名学生的成绩,并将成绩按照 , , , , 分成了5组.制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
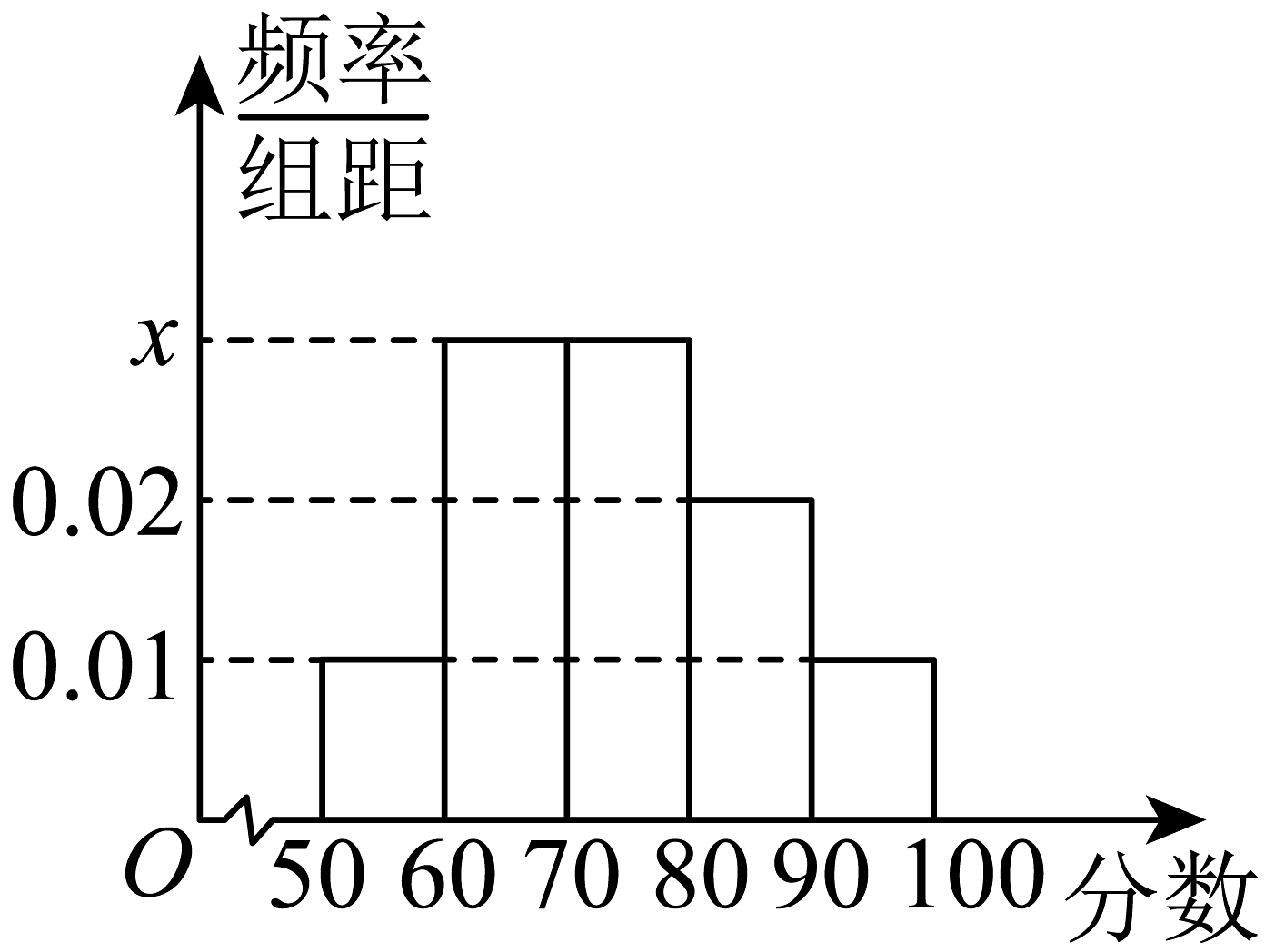 (1)、求频率分布直方图中的x的值:(2)、估计所抽取的100名学生成绩的平均数、中位数;(同一组中的数据用该组所在区间的中点值作代表)(3)、若按人数比例用分层随机抽样的方法从样本中成绩不低于70分的学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求成绩在内的至少有2人被抽到的概率.
(1)、求频率分布直方图中的x的值:(2)、估计所抽取的100名学生成绩的平均数、中位数;(同一组中的数据用该组所在区间的中点值作代表)(3)、若按人数比例用分层随机抽样的方法从样本中成绩不低于70分的学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求成绩在内的至少有2人被抽到的概率. -
8、已知为单位向量,且与的夹角为60°.(1)、求的值;(2)、若向量与的夹角为锐角,求实数的取值范围.
-
9、如图,在直三棱柱中, , , , 点是的中点.
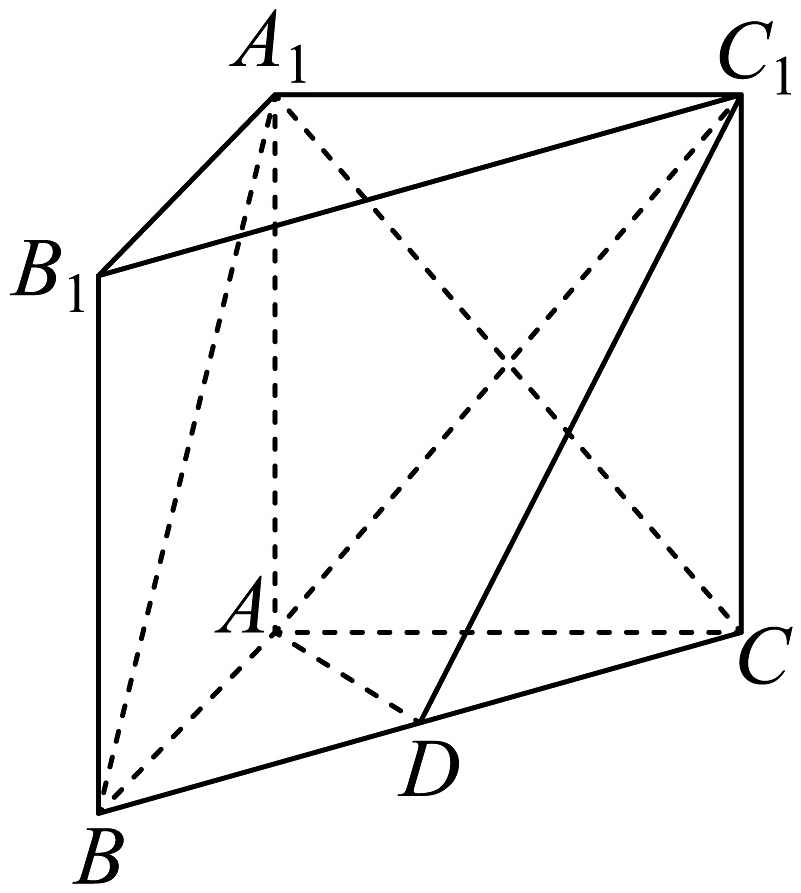 (1)、求证:平面;(2)、求二面角的正切值.
(1)、求证:平面;(2)、求二面角的正切值. -
10、某圆锥的侧面展开图是半径为4,圆心角为的扇形,则该圆锥的底面直径为 .
-
11、中国四大名楼是一种泛称,特指山西永济鹳雀楼、江西南昌滕王阁、湖北武汉黄鹤楼、湖南岳阳岳阳楼.记事件“只去黄鹤楼”,事件“至少去两个名楼”,事件“只去一个名楼”,事件“一个名楼也不去”,事件“至多去一个名楼”,则下列命题正确的是( )A、E与H是互斥事件 B、F与I是互斥事件,且是对立事件 C、 D、
-
12、甲、乙两人独立地破译一份密码,已知各人能破译的概率分别为 , 则甲、乙两人一起破译这份密码,密码被成功破译的概率为( )A、 B、 C、 D、
-
13、如图,在四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )
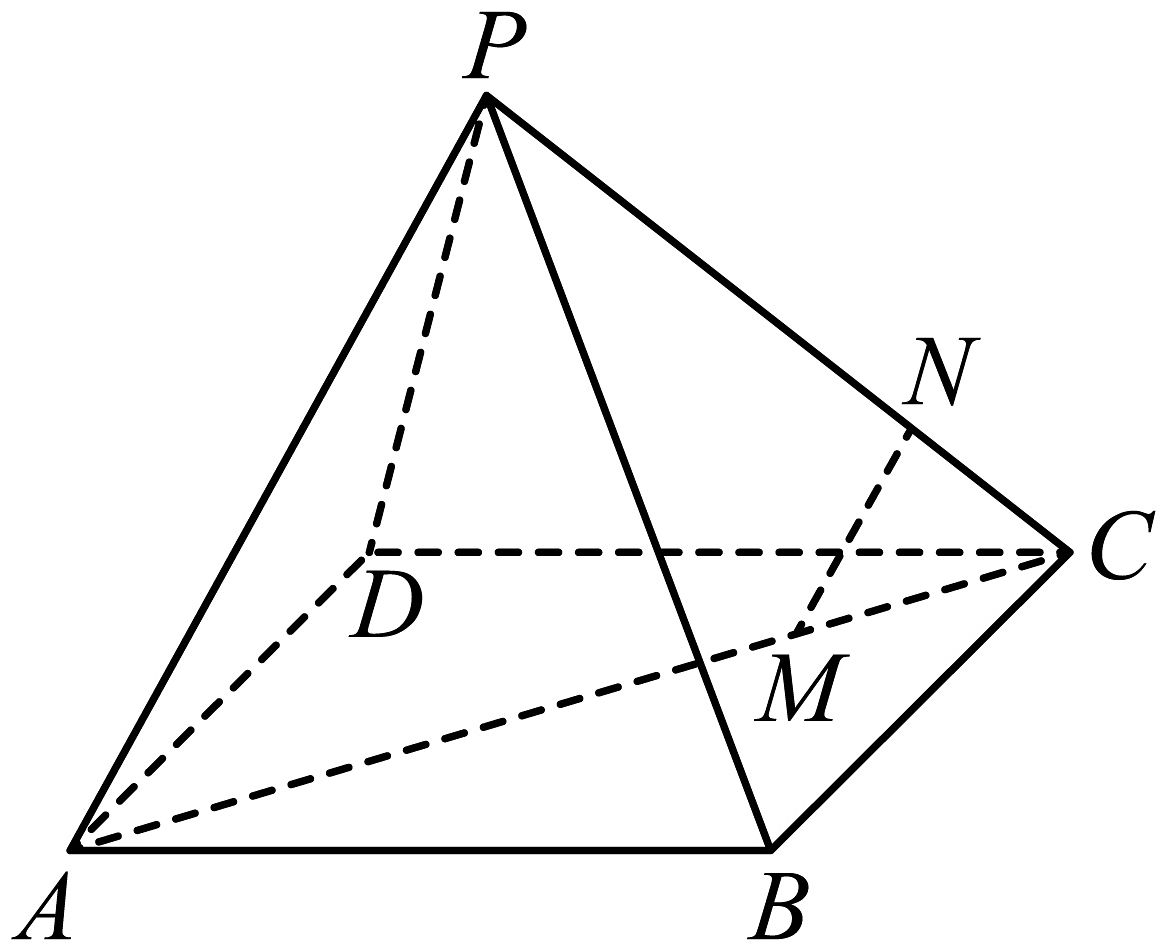 A、MN∥PD B、MN∥PA C、MN∥AD D、以上均有可能
A、MN∥PD B、MN∥PA C、MN∥AD D、以上均有可能 -
14、下列几何体中,不是旋转体的是( )A、
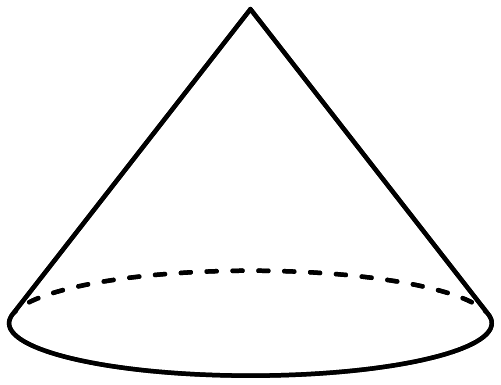 B、
B、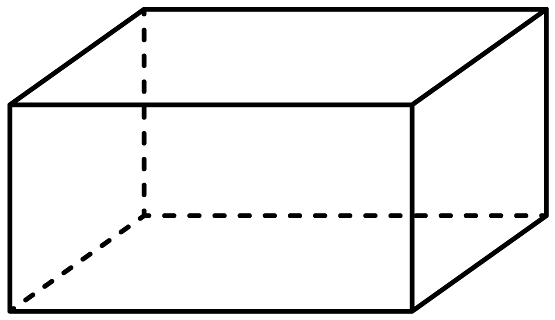 C、
C、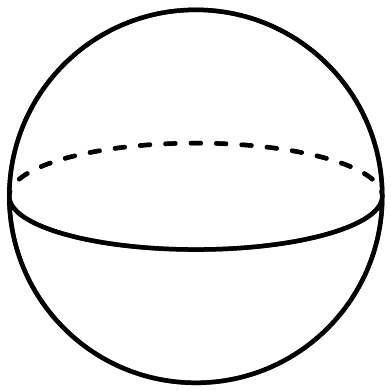 D、
D、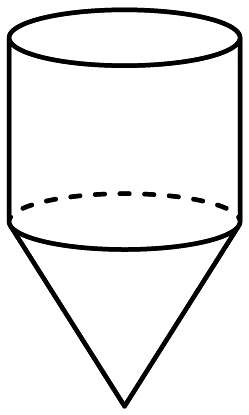
-
15、复数 , 则复数的虚部是( )A、 B、2 C、 D、1
-
16、已知函数是定义在上的奇函数,且 , 若对于任意两个实数 , 且 , 不等式恒成立,则不等式的解集为( )A、 B、 C、 D、
-
17、数列的一个通项公式为( )A、 B、 C、 D、
-
18、若恒成立,则实数 .
-
19、随着“一带一路”的发展,中国同某国贸易频繁,现统计近5年两国交易额(单位:百亿元),结果见表:
年份
2020
2021
2022
2023
2024
年份代码x
1
2
3
4
5
交易额y
9
12
17
21
26
(1)、统计学中常用线性相关系数r来衡量两个变量y与x之间线性关系的强弱.一般认为:若 , 则负相关性很强;若 , 则正相关性很强;若 , 则相关性一般;若 , 则相关性很弱.请用表中数据计算出r,并说明y与x的线性相关程度.(2)、求出y关于x的线性回归方程,并预测2025年两国的交易额.参考数据:;
参考公式:;回归方程 , , .
-
20、已知函数 .(1)、求函数的单调区间.(2)、求函数在上的值域.