相关试卷
-
1、已知函数 , 若 , , 满足 , 记 , 则的取值范围为 .
-
2、已知不等式的解集为 , 则 , 函数的单调递增区间为.
-
3、函数的定义域为 .
-
4、函数在 , 上有定义,若对任意 , , , 有 , 则称在 , 上具有性质 . 设在 , 上具有性质 , 下列命题正确的有A、在 , 上的图象是连续不断的 B、在 , 上具有性质 C、若在处取得最大值1,则 , , D、对任意 , , , , , 有
-
5、下列说法中正确的有( )A、若函数的定义域为 , 则函数的定义域为 B、函数和函数表示同一个函数 C、函数的值域为 D、函数满足 , 则
-
6、已知 , , 且 , 则的最小值为( )A、9 B、10 C、11 D、13
-
7、函数的图象大致是( )A、
 B、
B、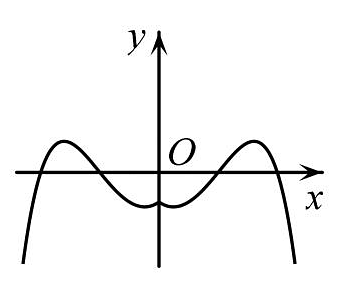 C、
C、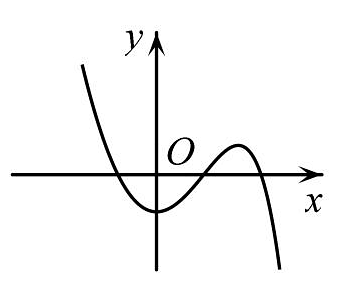 D、
D、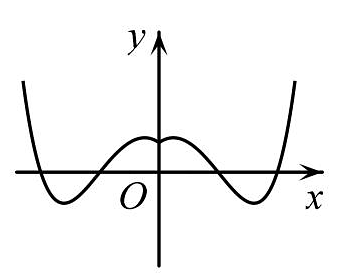
-
8、下列函数中,既是奇函数又在上单调递减的函数是( )A、 B、 C、 D、
-
9、已知集合 , 则( )A、 B、 C、 D、
-
10、已知全集 , 集合 , .(1)、当时,求;(2)、若 , 求实数的取值范围.
-
11、已知函数 , 且 .(1)、求m的值;(2)、证明:为奇函数;(3)、判断在上的单调性,并给予证明.
-
12、已知函数
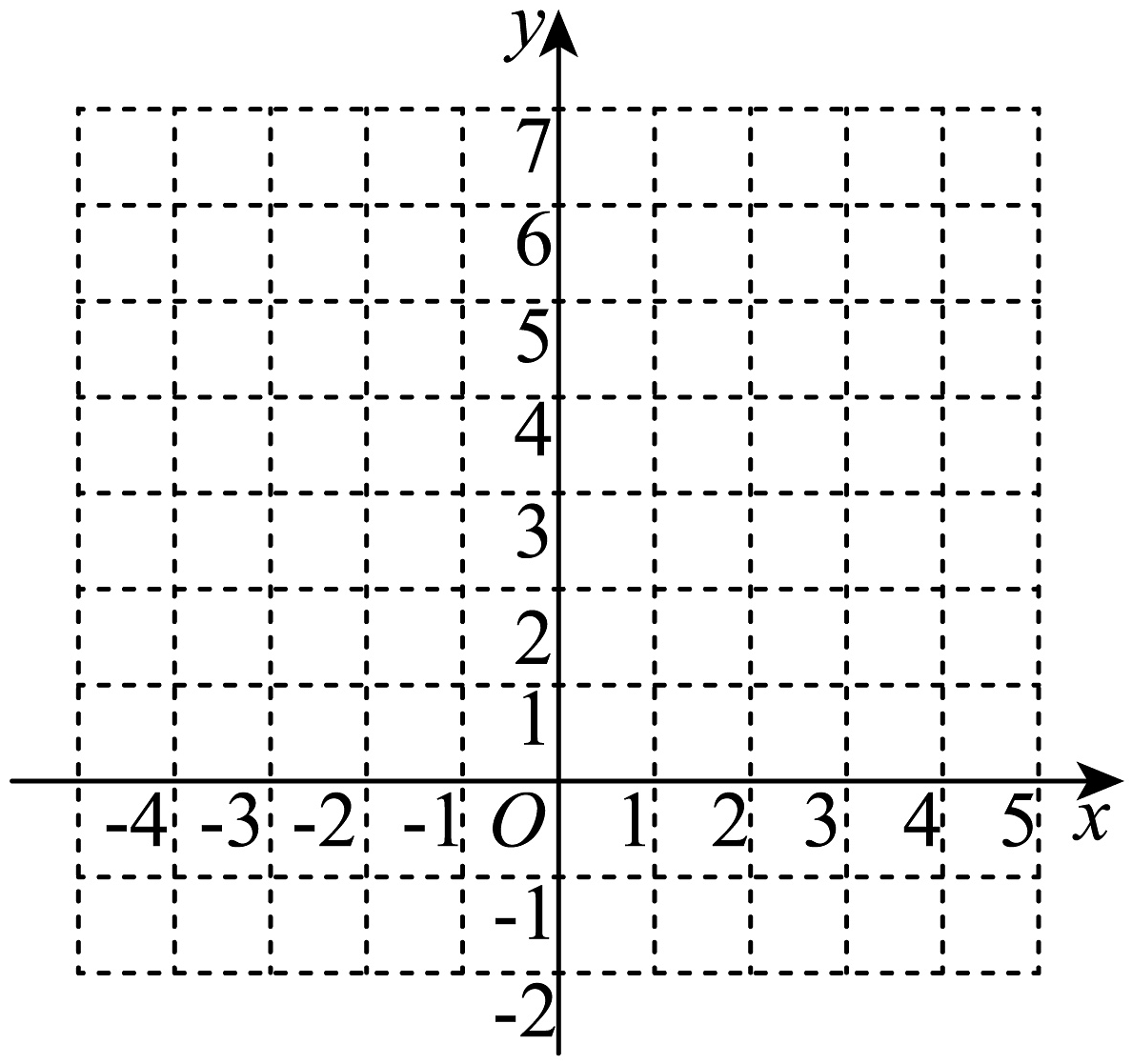 (1)、求;(2)、画出函数的图像;(3)、若 , 求的取值范围.
(1)、求;(2)、画出函数的图像;(3)、若 , 求的取值范围. -
13、已知全集 , 集合 ,
(1)求和
(2)求
-
14、对恒成立,则实数的范围为.
-
15、已知函数 , 若对任意的 , 不等式恒成立,则实数的取值范围是( )A、 B、 C、 D、
-
16、下列函数是偶函数,且在上单调递增的是( )A、 B、 C、 D、
-
17、“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
18、函数的定义域是( )A、 B、 C、 D、
-
19、为数列的前项和.已知 , .(1)、证明是等比数列,并求数列的通项公式;(2)、数列满足 , 求数列的前项和.
-
20、已知圆:与圆的公共弦所在的直线是: , 且圆的圆心在轴上.(1)、求圆的方程;(2)、若直线与圆相切,且在两条坐标轴上的截距相等,求直线的方程.