相关试卷
-
1、如图所示,正方体的棱长为1,点 , , 分别为 , , 的中点,则下列说法正确的是( )
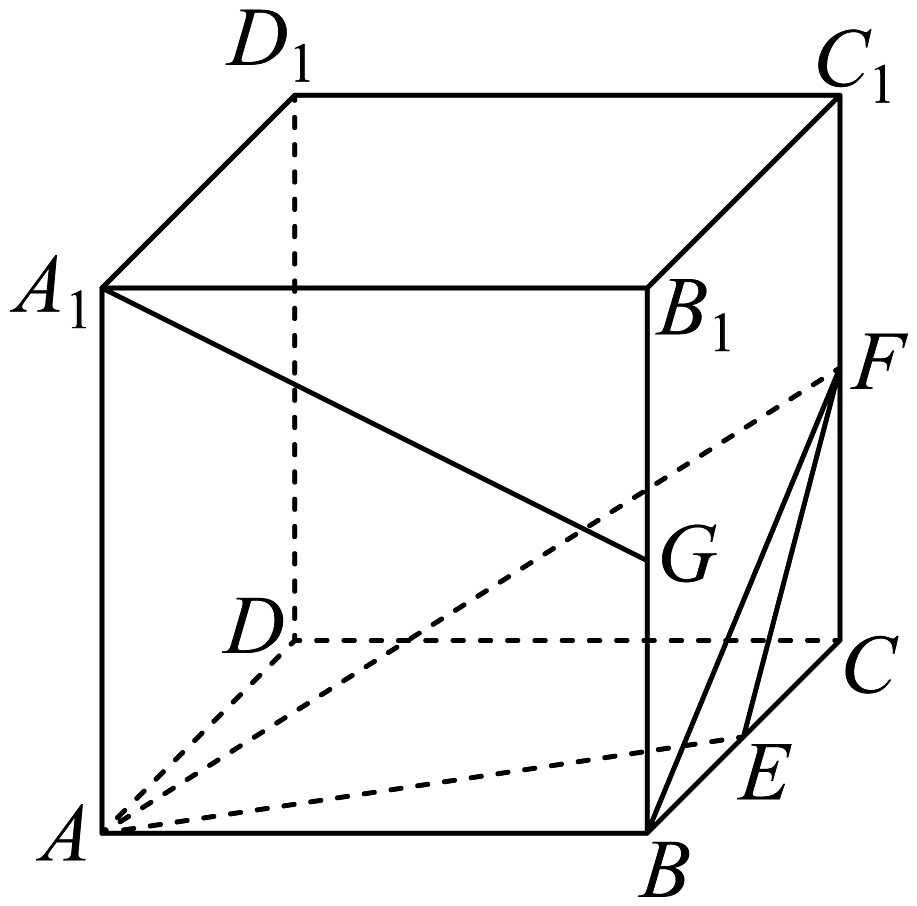 A、直线与直线垂直 B、三棱锥的体积为 C、直线与平面平行 D、直线与平面所成的角为
A、直线与直线垂直 B、三棱锥的体积为 C、直线与平面平行 D、直线与平面所成的角为 -
2、方程表示椭圆的充要条件是( )A、 B、 C、 D、或
-
3、空间四边形中, , , , 点在上,且为中点,为中点,则等于( )A、 B、 C、 D、
-
4、若点在圆的内部,则实数的取值范围是( )A、 B、 C、 D、
-
5、已知函数(1)、若 , 判断的奇偶性,求的最大值;(2)、若的最大值为 , 求的最小值.
-
6、某租赁公司,购买了一辆小型挖掘机进行租赁.据市场分析,该小型挖掘机的租赁利润(单位:万元)与租赁年数的关系为.(1)、该挖掘机租赁到哪几年时,租赁的利润超过万元?(2)、该挖掘机租赁到哪一年时,租赁的年平均利润最大?
-
7、设函数 , 其图像过点(1)、求出的解析式;(2)、判断函数在上的单调性,并用定义证明.
-
8、已知集合(1)、若 , 求;(2)、若 , 求实数的取值范围.
-
9、已知函数 , , 若对任意的 , 总存在 , 使成立,则实数的取值范围是 .
-
10、已知正数 , 满足: , 则的最小值为.
-
11、下列各组函数中,两个函数为同一函数的是( )A、和 B、和 C、和 D、和
-
12、设x,y为实数,满足 , 则下列结论正确的是( )A、 B、 C、 D、
-
13、已知 , 则取最大值时的值为( )A、 B、 C、 D、
-
14、函数的定义域为( )A、 B、 C、 D、
-
15、设集合 , 集合 , 则集合( )A、 B、 C、 D、
-
16、牛顿在《流数法》一书中,给出了代数方程的一种数值解法——牛顿法.具体做法如下:如图,设r是的根,首先选取作为r的初始近似值,若在点处的切线与x轴相交于点 , 称是r的一次近似值;用替代重复上面的过程,得到 , 称是r的二次近似值;一直重复,可得到一列数: , , , …, , ….在一定精确度下,用四舍五入法取值,当近似值相等时,该值即作为函数的一个零点r.
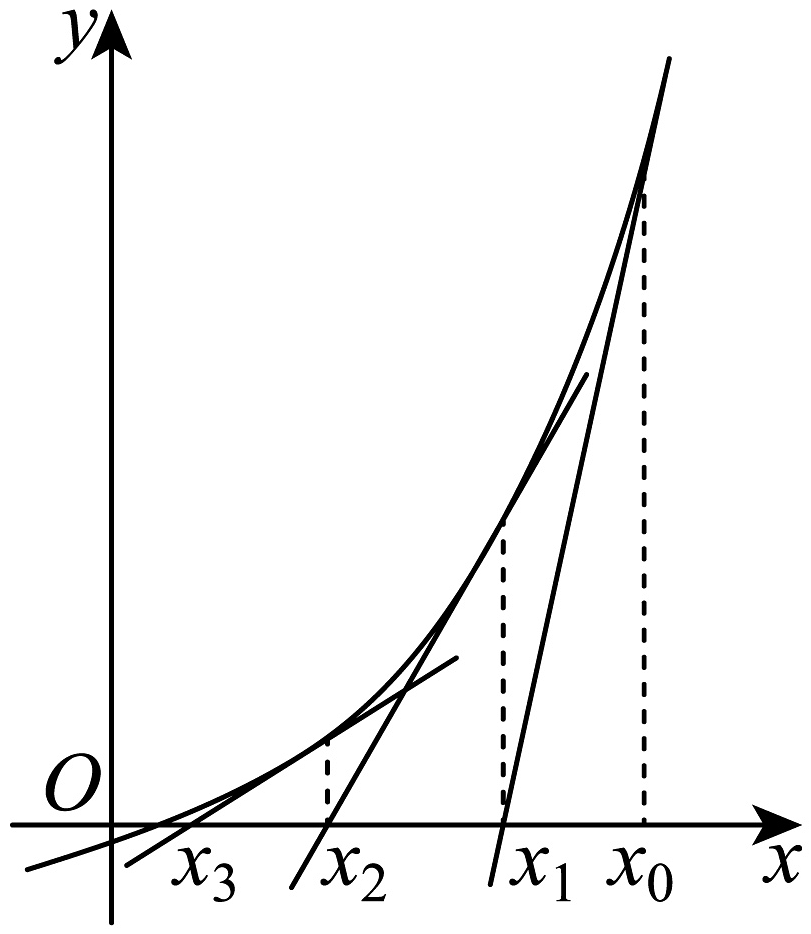 (1)、若 , 当时,求方程的二次近似值(保留到小数点后一位);(2)、牛顿法中蕴含了“以直代曲”的数学思想,直线常常取为曲线的切线或割线,求函数在点处的切线,并证明:;(3)、若 , 若关于x的方程的两个根分别为 , , 证明:.
(1)、若 , 当时,求方程的二次近似值(保留到小数点后一位);(2)、牛顿法中蕴含了“以直代曲”的数学思想,直线常常取为曲线的切线或割线,求函数在点处的切线,并证明:;(3)、若 , 若关于x的方程的两个根分别为 , , 证明:. -
17、已知函数在处取得极大值.(1)、求a的值;(2)、若有且只有3个零点,求实数b的取值范围.
-
18、已知的内角A,B,C的对边分别为a,b,c,且(1)、求角A的大小;(2)、若 , , 求的面积.
-
19、已知函数 , 方程有六个不相等实根,则实数b的取值范围是 .
-
20、设实数 , 若对不等式恒成立,则m的取值范围为 .