版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、拋物线 $x^{2} = 2 y$ 的准线方程是（）

A、 $x = \frac{1}{8}$ B、 $x = - \frac{1}{8}$ C、 $y = \frac{1}{2}$ D、 $y = - \frac{1}{2}$

查看解析
2、已知 $\vec{a} = (0, 2, 1), \vec{b} = (1, 4, - 1)$ ，则 $| \vec{a} - \vec{b} | =$ （）

A、2 B、 $\sqrt{5}$ C、3 D、 $\sqrt{37}$

查看解析
3、直线 $2 x - 2 \sqrt{3} y + 5 = 0$ 的倾斜角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看解析
4、已知函数 $f (x)$ 的定义域为 $D$ ，若最多存在 $n$ 个实数 $x_{1}$ ， $x_{2}$ ， $\dots$ ， $x_{n} \in D$ ， $(x_{1} < x_{2} < \dots < x_{n})$ ，使得 $f (x_{1}) = f (x_{2}) = \dots = f (x_{n})$ ， $(n \geq 2, n \in N^{*})$ ，则称函数 $f (x)$ 为“ $n$ 级 $E$ 函数”.

(1)、函数① $f (x) = x^{- 2}$ ， ② $g (x) = \frac{1}{x}$ 是否为“ $n$ 级 $E$ 函数”，如果是，求出 $n$ 的值，如果不是，请说明理由；

(2)、若函数 $f (x) = |x^{2} - 3 x + t|$ ，求 $x_{1} + x_{2} + \dots + x_{n}$ 的值；

(3)、若函数 $f (x) = x^{2} + x |x + a| (a > 0)$ ，求 $\frac{x_{1}}{x_{2}} + x_{1}$ ， $(x_{2} \neq 0)$ 的取值范围.（用 $a$ 表示）

查看解析
5、设函数 $f (x) = a x^{2} + b x + c (a \neq 0, b, c \in R)$ .

(1)、若 $f (1) = - a$ ，求证： $f (x)$ 在 $[0, 2]$ 内存在零点；

(2)、若不等式 $f (x) < 0$ 的解集是 $(- 2, - 1)$ ，且 $x \in [1, 2]$ 时， $f (2^{x}) \leq 4^{x}$ 恒成立，求 $a$ 的取值范围.

查看解析
6、设奇函数 $f (x) = \ln |\frac{2 e}{x + 1} - e| + b$ ，（ $e$ 为自然对数的底数， $e \approx 2.71828 \dots$ ）.

(1)、求 $f (x)$ 的定义域和 $b$ ；

(2)、 $x \in (\frac{1 - e}{1 + e}, 1)$ ，求函数 $f (x)$ 的值域.

查看解析
7、若函数 $f (x) = a^{a x + \frac{1}{x}}$ ，（ $a > 0$ ，且 $a \neq 1$ ）在区间 $(\frac{1}{2}, 2)$ 上单调递增，则 $a$ 的取值范围是

查看解析
8、已知 $f (x) = |lg x|$ ，若 $f (a) = f (b)$ ， $(a < b)$ ，则 $2 a + b$ 的最小值为.

查看解析
9、已知集合 $A = \{1, 3, m^{2}\}$ ， $B = \{1, m + 2\}$ ，若 $A \cup B = A$ ，则实数 $m$ 的值为.

查看解析
10、若函数 $f (x) = x |x| + a x + b$ ，当 $x \in [- 2, 2]$ 时， $f (x)$ 的最大值为 $M$ ，最小值为 $m$ ；则下列说法正确的是（）

A、 $M - m$ 的值与 $b$ 无关 B、 $M - m$ 的值与 $a$ 无关 C、函数 $f (x)$ ， $x \in R$ 至少有一个零点 D、函数 $f (x)$ ， $x \in R$ 至多有三个零点

查看解析
11、波恩哈德·黎曼（1866.07.20~1926.09.17）是德国著名的数学家.他在数学分析、微分几何方面作出过重要贡献，开创了黎曼几何，并给后来的广义相对论提供了数学基础.他提出了著名的黎曼函数，该函数的定义域为 $[0, 1]$ ，其解析式为： $R (x) = \{\begin{array}{l} \frac{1}{q}, x = \frac{p}{q} (p, q 为正整数且 p, q 互质) \\ 0, x = 0 或 1 或 (0, 1) 内的无理数 \end{array}$ ，下列关于黎曼函数的说法正确的是（）

A、 $R (\frac{6}{7}) = \frac{1}{7}$ B、 $R (a) R (b) \leq R (a b)$ ， $a$ ， $b \in [0, 1]$ C、 $R (x)$ 的值域为 $[0, \frac{1}{2}]$ D、 $y = R (x + \frac{1}{2})$ 为偶函数

查看解析
12、下列命题为真命题的是（）

A、若 $a > b$ ，则 $\frac{1}{a} > \frac{1}{b}$ B、若 $a > b > 0$ ， $c < d < 0$ ，则 $a c < b d$ C、若 $0 > c > a > b$ ，则 $\frac{a}{c - a} > \frac{b}{c - b}$ D、若 $a > b > c > 0$ ，则 $\frac{a}{b} > \frac{a + c}{b + c}$

查看解析
13、若集合 $A = {(m, n) ∣ m \leq - 2, 0 < n \leq t}$ 时， $\forall (m, n) \in A$ ，均有 $m {log}_{4} n - n - 3 m \geq 0$ 恒成立，则 $t$ 的最大值为（）

A、1 B、4 C、16 D、64

查看解析
14、已知函数 $f (x)$ 的定义域为 $R$ ， $y = f (x) - 2 e^{x} - 1$ 是奇函数， $y = f (x) - 4 e^{- x}$ 为偶函数，（ $e$ 为自然对数的底数， $e \approx 2.71828 \dots$ ），则 $f (x)$ 在区间 $[- 1, 0]$ 上的最小值为（）

A、2 B、3 C、 $\frac{3}{e} - e + 1$ D、 $3 e + 1 - \frac{1}{e}$

查看解析
15、图（1）是某条公共汽车线路收支差额 $y$ 关于乘客量 $x$ 的图象
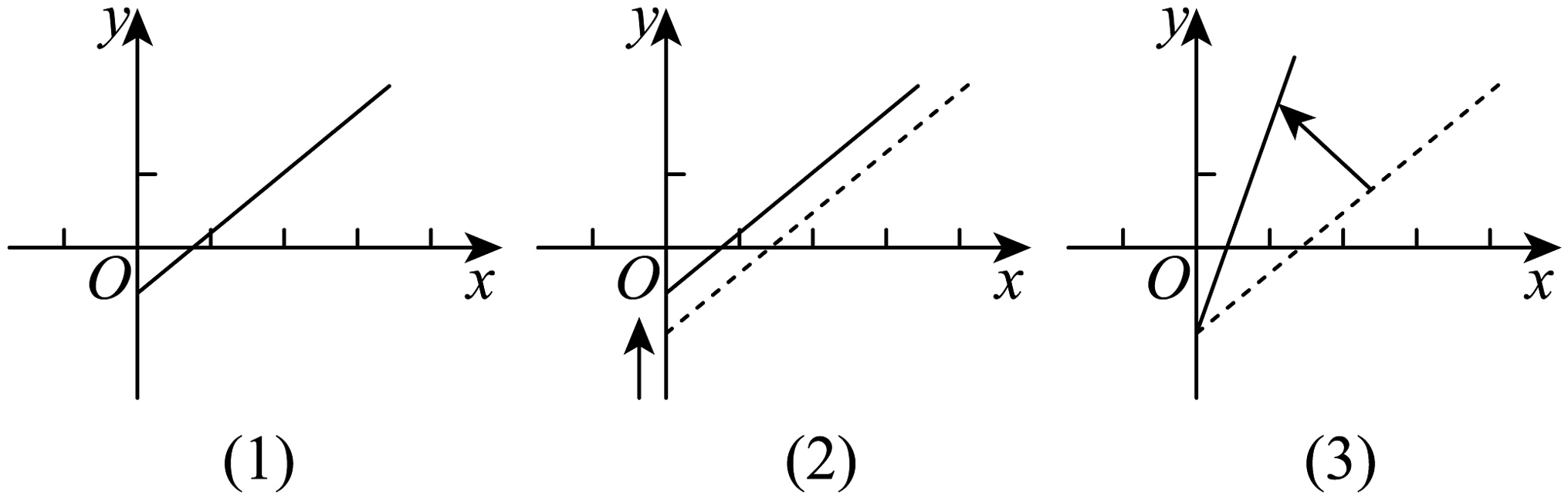
由于目前本条线路亏损，公司有关人员提出了两种扭亏为赢的建议，如图（2）（3）所示，这两种建议是（）

A、（2）：降低成本，票价不变；（3）：成本不变，提高票价. B、（2）：提高成本，票价不变；（3）：成本不变，降低票价. C、（2）：成本不变，提高票价；（3）：提高成本，票价不变. D、（2）：降低成本，提高票价；（3）：降低成本，票价不变.

查看解析
16、对于集合 $A$ ， $B$ 和全集 $U$ ， “ $A \cap (∁_{U} B) = \emptyset$ ”是“ $A \subseteq B$ ”的什么条件（）

A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件

查看解析
17、如图，①②③④中不属于函数 $y = 2^{x}$ ， $y = 3^{x}$ ， $y = {(\frac{1}{2})}^{x}$ 的一个是（）

A、① B、② C、③ D、④

查看解析
18、设 $a > 0$ ，且 $a \neq 1$ ，则下列运算中正确的是（）

A、 $a^{\frac{4}{3}} a^{\frac{3}{4}} = a$ B、 $a^{\log_{a} \sqrt{a}} = \frac{1}{2}$ C、 $\log_{a} 2 = - \log_{2} a$ D、 $\frac{\sqrt{a} \sqrt[3]{a} \sqrt[4]{a}}{{(\sqrt[6]{a})}^{5} a^{\frac{1}{4}}} = 1$

查看解析
19、已知点P( $\sqrt{2}$ ＋1，2－ $\sqrt{2}$ )，点M(3，1），圆C：(x－1)²＋(y－2)²＝4.
（1）求过点P的圆C的切线方程；
（2）求过点M的圆C的切线方程，并求出切线长．

查看解析
20、经过点 $P (4, - 2)$ 的抛物线的标准方程为（）

A、 $y^{2} = x$ B、 $x^{2} = 8 y$ C、 $x^{2} = - 8 y$ D、 $y^{2} = - 8 x$

查看解析

上一页 948 949 950 951 952 下一页跳转