相关试卷
-
1、已知复数满足 , 则( )A、3 B、2 C、1 D、
-
2、已知集合 , 且 , 则.
-
3、已知某校共有1000名学生参加体能达标测试,现从中随机抽取100名学生的成绩,将他们的测试成绩(满分:100分)分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],得到如下频数分布表.
成绩/分
[40,50)
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
10
15
20
30
15
10
(1)求这100名学生的体能测试平均成绩(同一组中的数据用该组区间的中点值为代表).
(2)在这100名学生中,规定:测试成绩不低于80分为“优秀”,成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为体能测试成绩是否优秀与性别有关?
优秀
非优秀
总计
男生
30
女生
50
总计
(3)根据样本数据,可认为该校全体学生的体能测试成绩X近似服从正态分布N(μ,14.312),其中μ近似为样本平均数 , 则这1000名学生中体能测试成绩不低于84.81分的估计有多少人?
参考公式及数据:X~N(μ,σ2),P(μ-σ≤X<μ+σ)≈0.6827,P(μ-2σ≤X<μ+2σ)≈0.9545;
, 其中n=a+b+c+d.
P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
-
4、某革命老区县因地制宜的将该县打造成“生态水果特色小县”.该县某水果树的单株产量(单位:千克)与施用肥料x(单位:千克)满足如下关系: , 且单株施用肥料及其它成本总投入为元.已知这种水果的市场售价为10元/千克.在国务院关于新时代支持革命老区振兴发展的意见,支持发展特色农业产业的保障下,该县水果销路畅通.记该水果树的单株利润为(单位:元).(1)、求函数的解析式;(2)、当施用肥料为多少千克时,该水果树的单株利润最大?最大利润是多少?
-
5、函数的定义域为 , 若对满足的任意、 , 均有 , 则称函数具有“性质”,已知 , 且函数具有性质,则实数的取值范围为 .
-
6、已知函数在区间内单调递减,则的最大值为 .
-
7、当时,曲线与交点的个数为 .
-
8、函数的图象如图所示,将其向左平移个单位长度,得到的图象,则下列说法正确的是( )
 A、 B、函数的图象关于点对称 C、函数的图象关于直线对称 D、函数在上单调递减
A、 B、函数的图象关于点对称 C、函数的图象关于直线对称 D、函数在上单调递减 -
9、在的二项展开式中,以下判断正确的是( )A、所有项的系数之和为1024 B、各二项式系数之和为32 C、第3项系数最大 D、常数项的值为90
-
10、设 , 将的图像向右平移个单位,得到的图像,设 , , 则的最大值为( )A、 B、 C、 D、
-
11、当变动时,动直线围成的封闭图形的面积为( )A、 B、 C、 D、
-
12、一位语文老师在网上购买了四书五经各一套,四书指《大学》《中庸》《论语》《孟子》,五经指《诗经》《尚书》《礼记》《周易》《春秋》,他将9本书整齐地放在同一层书架上,若四书,五经必须分别排在一起,且《大学》和《春秋》不能相邻,则不同方式的排列种数为( )A、5760 B、5660 C、5642 D、5472
-
13、不等式对任意恒成立,则的最小值为( )A、 B、2 C、 D、
-
14、已知圆过 , 两点,且圆心在直线上.(1)、求圆的方程;(2)、设直线与圆交于A,两点,在直线上是否存在定点 , 使得直线 , 的倾斜角互补?若存在,求出点的坐标;若不存在,说明理由.
-
15、已知顶点 , , .(1)、求边BC上的高所在直线的方程;(2)、若直线l过点A,且l的纵截距是横截距的2倍,求直线l的方程.
-
16、如图,已知二面角的大小为 , , , , 且 , , 则.

-
17、如图,点是棱长为2的正方体的表面上一个动点,则( )
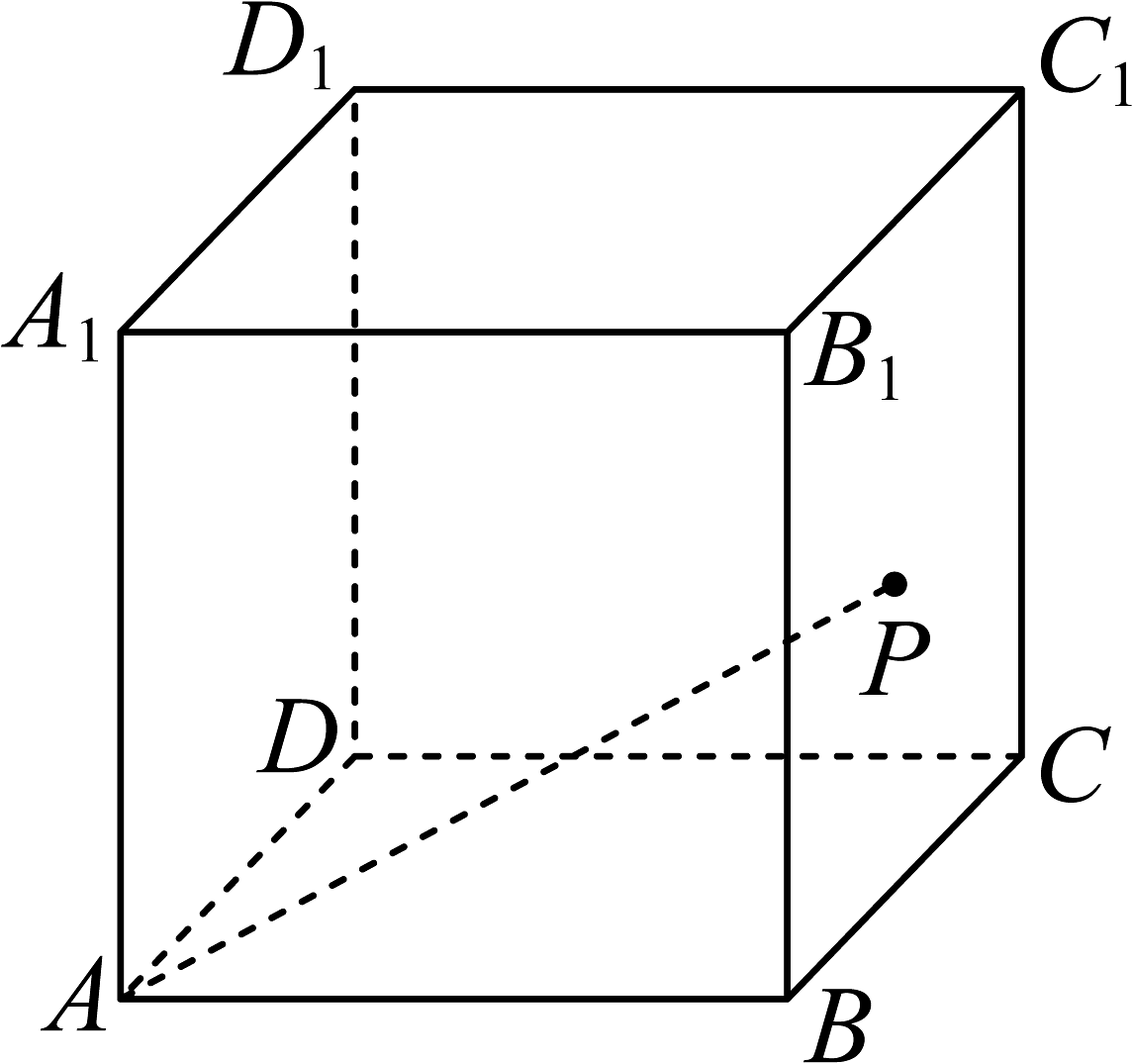 A、当在平面上运动时,三棱锥的体积为定值 B、当在线段上运动时,与所成角的取值范围是 C、若是的中点,当在底面上运动,且满足平面时,长度的最小值是 D、使直线与平面所成的角为的点的轨迹长度为
A、当在平面上运动时,三棱锥的体积为定值 B、当在线段上运动时,与所成角的取值范围是 C、若是的中点,当在底面上运动,且满足平面时,长度的最小值是 D、使直线与平面所成的角为的点的轨迹长度为 -
18、数列的前n项和为 , 且.(1)、求证:数列为等比数列,并求其通项公式;(2)、令 , 数列的前n项和为.求证:.
-
19、已知函数满足 , 且在上是增函数,则 , , 的大小顺序是( )A、 B、 C、 D、
-
20、为了加深师生对党史的了解,激发广大师生知史爱党、爱国的热情,我校举办了“学党史、育文化”暨“喜迎党的生日”党史知识竞赛,并将名师生的竞赛成绩(满分分)整理成如图所示的频率直方图.
 (1)、求频率直方图中的值以及师生竞赛成绩的中位数(2)、从竞赛成绩在 , 的师生中,采用分层抽样的方法抽取人,再从抽取的人中随机抽取人,求人的成绩来自同一区间的概率.
(1)、求频率直方图中的值以及师生竞赛成绩的中位数(2)、从竞赛成绩在 , 的师生中,采用分层抽样的方法抽取人,再从抽取的人中随机抽取人,求人的成绩来自同一区间的概率.