相关试卷
-
1、若数列满足 , , 则数列的前n项和最大时,n的值为( )A、6 B、7 C、8 D、9
-
2、数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.因为运算,数的威力无限;没有运算,数就只是一个符号.对数运算与指数幂运算是两类重要的运算.
(1)对数的运算性质降低了运算的级别,简化了运算,在数学发展史上是伟大的成就.对数运算性质的推导有很多方法.请同学们根据所学知识推导如下的对数运算性质:如果 , 且 , , 那么;
(2)请你运用上述对数运算性质计算的值;
(3)因为 , 所以的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断的位数.(注)
-
3、设数列的前项和为 , 且满足 , .
(1)求(用表示);
(2)求证:当时,不等式成立.
-
4、在平面直角坐标系中,已知角的终边与以原点为圆心的单位圆交于点.
(1)请写出 , , 的值;
(2)若角满足.
(ⅰ)计算的值;
(ⅱ)计算的值.
-
5、设数列的前项和为 , 若 , 且 , 则.
-
6、半径为的圆的一段弧长等于 , 则这段弧所对圆心角的弧度数为 .
-
7、设等比数列的公比为 , 其前项和为 , 前项积为 , 并且满足条件 , 则下列结论正确的是( )A、 B、 C、的最大值为 D、的最大值为
-
8、下列函数中,最小值为2的是A、 B、 C、 D、
-
9、若直线是函数图象的一条切线,则函数可以是( )A、 B、 C、 D、
-
10、设函数在定义域内可导,的图象如图所示,则导函数的图象为( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
11、若数列满足:对任意的 , 总存在 , 使 , 则称是“数列”.现有以下数列:①;②;③;④;其中是数列的有( ).A、①③ B、②④ C、②③ D、①④
-
12、著名物理学家李政道说:“科学和艺术是不可分割的”.音乐中使用的乐音在高度上不是任意定的,它们是按照严格的数学方法确定的.我国明代的数学家、音乐理论家朱载填创立了十二平均律是第一个利用数学使音律公式化的人.十二平均律的生律法是精确规定八度的比例,把八度分成13个半音,使相邻两个半音之间的频率比是常数,如下表所示,其中表示这些半音的频率,它们满足.若某一半音与的频率之比为 , 则该半音为( )
频率
半音
C
D
E
F
G
A
B
C(八度)
A、 B、G C、 D、A -
13、函数的定义域为A、 B、 C、 D、
-
14、已知集合 , , 则=A、 B、 C、 D、
-
15、已知函数是定义在上的偶函数,当时, . 现已画出函数在轴右侧的图象,如图所示.
 (1)、画出函数在轴左侧的图象,根据图象写出函数在上的单调区间;(2)、求函数在上的解析式;(3)、解不等式.
(1)、画出函数在轴左侧的图象,根据图象写出函数在上的单调区间;(2)、求函数在上的解析式;(3)、解不等式. -
16、已知函数的图象与的图象关于直线对称.(1)、求函数的解析式;(2)、若在定义域内恒成立,求的取值范围;(3)、求证:.
-
17、已知集合 , , 则图中阴影部分表示的集合为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、如图,在矩形中, , 取中点 , 将和分别沿直线 , 折叠,使 , 两点重合于点得到三棱锥 .
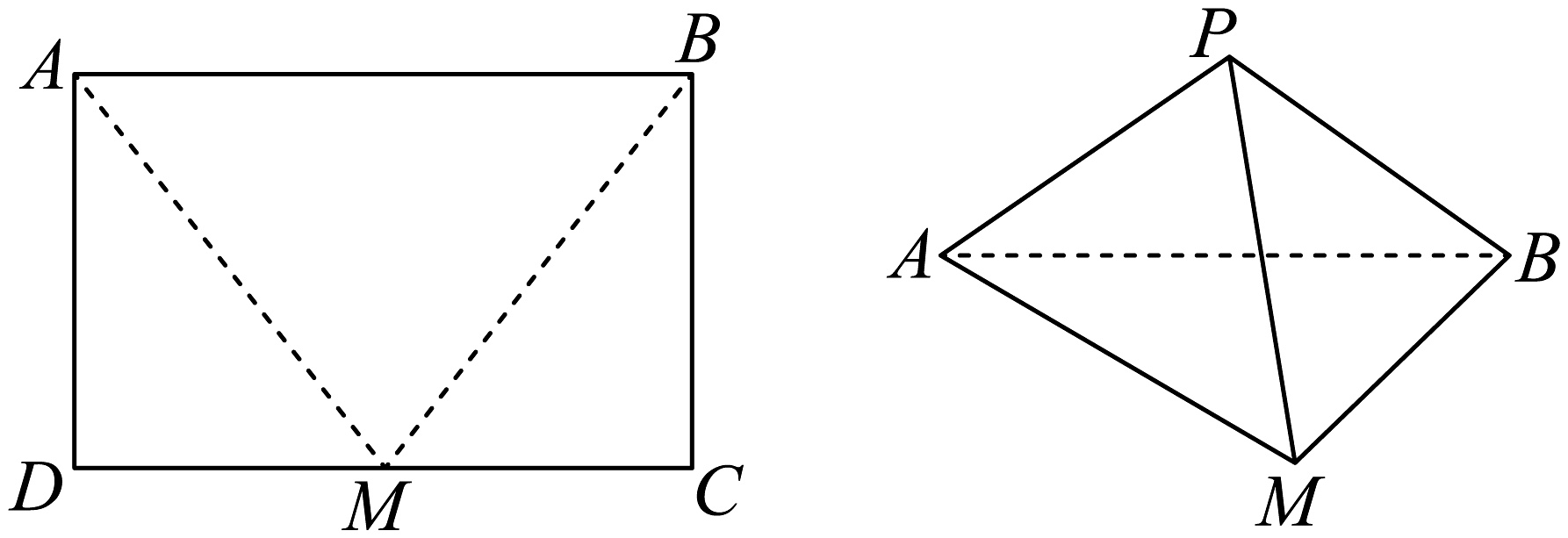 (1)、当时,求证:;(2)、若二面角的平面角为 , 是否存在上一点 , 使得与平面所成角的正弦值为?若存在,请求出点的位置;若不存在,请说明理由.
(1)、当时,求证:;(2)、若二面角的平面角为 , 是否存在上一点 , 使得与平面所成角的正弦值为?若存在,请求出点的位置;若不存在,请说明理由. -
19、若直线与曲线C:有两个不同的公共点,则k的取值范围是( )A、 B、 C、 D、
-
20、如图,在棱长为的正方体中, , 分别是 , 的中点,为上一点.
 (1)、求证:;(2)、求点到平面的距离;(3)、当为何值时,平面与平面所成的夹角的余弦值为.
(1)、求证:;(2)、求点到平面的距离;(3)、当为何值时,平面与平面所成的夹角的余弦值为.