相关试卷
-
1、已知椭圆和双曲线的焦点相同,则.
-
2、已知函数 , 则( )A、 B、当时, C、当时, D、当时,
-
3、已知 , , , , 其中 , 点为平面内一点,记点到 , 的距离分别为 , , 则下列条件中能使点的轨迹为椭圆的是( )A、 B、 C、 D、
-
4、观察下列散点图的分布规律和特点,其中两个变量存在相关关系的有( )A、
 B、
B、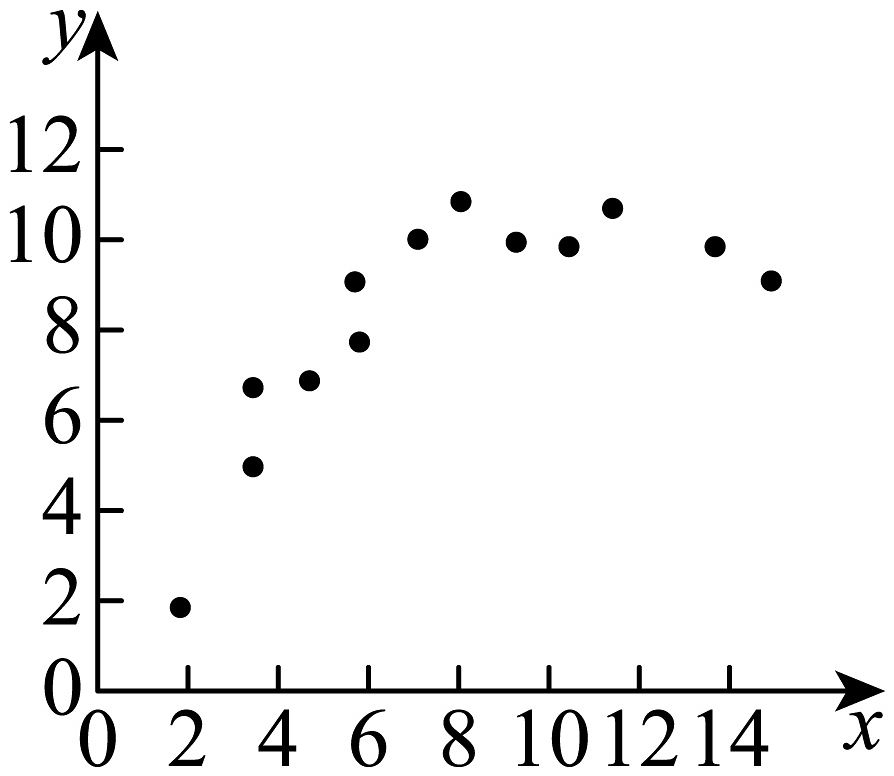 C、
C、 D、
D、
-
5、飞行棋是一种家喻户晓的竞技游戏,玩家根据骰子(骰子为均匀的正六面体)正面朝上的点数确定飞机往前走的步数,刚好走到终点处算“到达”,如果玩家投掷的骰子点数超出到达终点所需的步数,则飞机须往回走超出点数对应的步数.在一次游戏中,飞机距终点只剩3步(如图所示),设该玩家到达终点时投掷骰子的次数为 , 则( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
6、已知函数的值域为 , 则实数的取值范围为( )A、 B、 C、 D、
-
7、已知 , , 则( )A、 B、5 C、 D、
-
8、已知函数解集为 .(1)、求的解析式;(2)、用定义法证明函数在上为单调增函数;(3)、若在区间上恒成立,求实数的范围.
-
9、现有张形状相同的卡片,上而分别写有数字 , 将这张卡片充分混合后,每次随机抽取一张卡片,记录卡片上的数字后放回,现在甲同学随机抽取4次.(1)、若 , 求抽到的4个数字互不相同的概率;(2)、在统计学中,我们常用样本的均值来估计总体的期望.定义为随机变量的阶矩,其中1阶矩就是的期望 , 利用阶矩进行估计的方法称为矩估计.
(i)记每次抽到的数字为随机变量 , 计算随机变量的1阶矩和2阶矩;(参考公式:)
(ii)知甲同学抽到的卡片上的4个数字分别为 , 试利用这组样本并结合(i)中的结果来计算的估计值.(的计算结果通过四舍五入取整数)
-
10、已知函数.(1)、求的最值;(2)、求正整数 , 使其满足且;(3)、若 , 求证:.
-
11、如图,在三棱台中,分别是的中点,.
 (1)、求证:平面;(2)、若 , 求平面与平面所成二面角的正弦值.
(1)、求证:平面;(2)、若 , 求平面与平面所成二面角的正弦值. -
12、在平面直角坐标系中,椭圆的离心率是 , 上的点到两焦点的距离之和等于4.(1)、求椭圆的方程;(2)、过焦点作斜率为1的直线与椭圆相交于两点.求的面积.
-
13、在数列中,点在直线上;在等比数列中, , .(1)、求数列的通项公式;(2)、设 , 求数列的前项和.
-
14、已知边长为的等边三角形的一个顶点位于原点,另外两个顶点在抛物线上,则的方程是;设点在直线上,过点的两条直线分别与相切于两点,记直线的斜率分别为 , 则的最小值是.
-
15、一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数.在不超过30的质数中任取两个不同数,则其和是偶数的取法有种.
-
16、已知是等差数列的前项和,目 , 则.
-
17、已知函数.则( )A、当时,若有两个零点,则的值是或 B、若 , , 且 , 则的最小值是 C、对任意恒有 D、若存在极值点 , 且 , 其中 , 则
-
18、在中,角、、的对边分别为、、 , 若 , , , 则( )A、 B、外接圆半径 C、 , D、若是边中点,则
-
19、已知圆 , 直线 , 则( )A、当时,与圆相切 B、当时,被圆所截得的弦长为 C、对任意 , 与圆均有公共点 D、设与圆相交于不同两点 , 且 , 则
-
20、已知函数是偶函数,则( )A、 B、 C、 D、