相关试卷
-
1、为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度(单位:毫克/立方米)随着时间(单位:小时)变化的函数关系式近似为 . 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间约达几小时?(结果精确到0.1,参考数据: , )
(2)若第一次喷洒2个单位的净化剂,3小时后再喷洒2个单位的净化剂,设第二次喷洒小时后空气中净化剂浓度为(毫克/立方米),其中 .
①求的表达式;
②求第二次喷洒后的3小时内空气中净化剂浓度的最小值.
-
2、已知角()的顶点与原点重合,始边与轴的非负半轴重合,它的终边与单位圆交于点 .(1)、若角是由角的终边顺时针旋转得到的,求的值;(2)、若角满足 , 求的值.
-
3、已知函数是定义在上的奇函数,当时, .(1)、求函数的解析式;(2)、若 , 求函数的值域
-
4、计算:(1)、;(2)、 .
-
5、已知 , 则 .
-
6、函数的单调增区间为.
-
7、已知 , 都是定义在上的函数,对任意满足 , 且 , 则下列说法正确的有( )A、 B、函数的图象关于点对称 C、 D、若 , 则
-
8、已知函数 , 下列选项中正确的是( )A、的最小正周期为 B、的图象关于直线对称 C、在上单调递增 D、在上值域为
-
9、下列函数中,最小值等于4的函数是( )A、 B、 C、 D、
-
10、设若是的最小值,则的取值范围为A、 B、 C、 D、
-
11、函数在区间上有且仅有个零点,则实数ω有( )A、最大值 B、最大值 C、最小值 D、最小值
-
12、若对 , 恒成立,则的取值范围是( )A、 B、 C、 D、
-
13、已知 , 且 , 则( )A、 B、 C、 D、
-
14、设 , 则的大小关系是( )A、 B、 C、 D、
-
15、已知命题和命题 , 则是的( )A、充分不必要条件 B、必要不充分条件 C、既不充分也不必要条件 D、充要条件
-
16、若集合 , 则( )A、 B、 C、 D、
-
17、已知空间向量 , 且与垂直,则等于.
-
18、已知集合.(1)、集合 , 且中的任意三个不同的元素 , , 都有.
(i)当时,写出一个满足条件的恰有四个元素的集合;
(ii)对于任意给定的 , 求集合中的元素个数的最大值.
(2)、已知集合P={C|CA}, , 且同时满足以下条件:① , , 都有(其中 , , );② , , 使得(其中).求集合中的元素个数. -
19、如图,在三棱柱中,平面平面 , 平面.
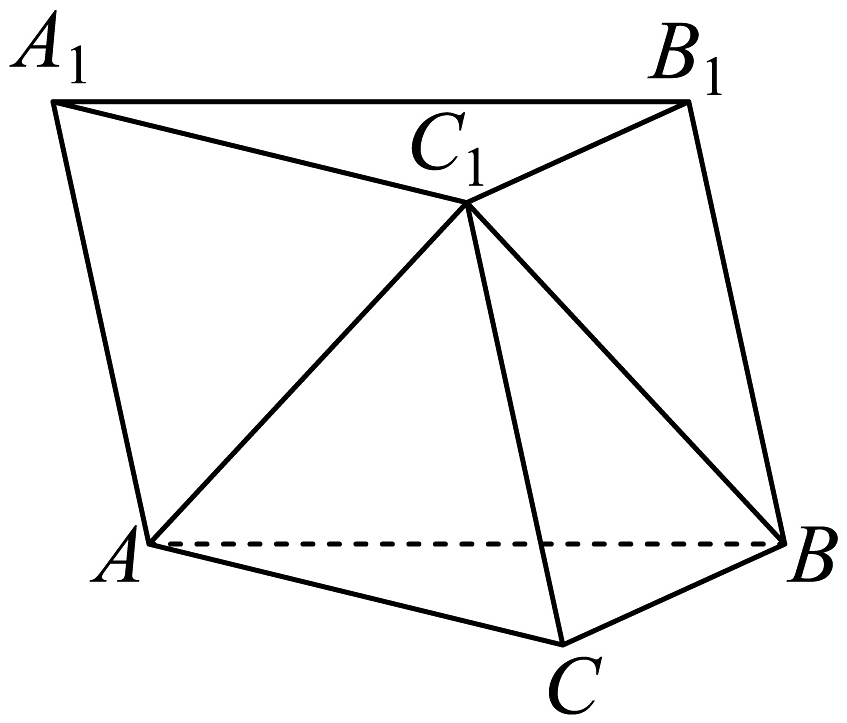 (1)、求证:;(2)、若二面角的正弦值为 , 且 , 求.
(1)、求证:;(2)、若二面角的正弦值为 , 且 , 求. -
20、如图所示的五面体为《九章算术》中记载的羡除,它指的是墓道或隧道.其中 , 四边形 , , 均为等腰梯形,平面平面 , , , , 和间的距离为2,和间的距离为4,则该羡除的体积为.
