相关试卷
-
1、函数在内恰有两个对称中心, , 将函数的图象向右平移个单位得到函数的图象.若 , 则( )A、 B、 C、 D、
-
2、函数的部分图象大致是( )A、
 B、
B、 C、
C、 D、
D、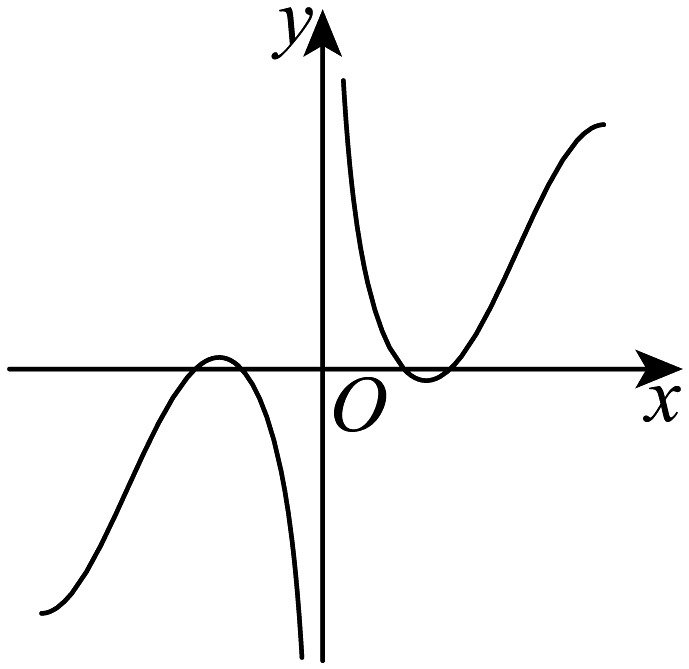
-
3、已知点是圆上任意一点,直线:分别与轴、轴相交于点 , 则( )A、直线与圆相离 B、面积的最小值为 C、的最大值为 D、的最小值为
-
4、若直线与圆O:相切,则圆与圆O( )A、相离 B、相交 C、内切 D、外切
-
5、已知函数 , 且 .(1)、求的值;(2)、若 , 判断的单调性,并根据定义证明;(3)、若函数存在零点,求的取值范围.
-
6、将正弦曲线向左平移个单位长度,再将所得曲线上每一点的横坐标伸长为原来的2倍(纵坐标不变),进一步将所得曲线上每一点的纵坐标扩大为原来的4倍(横坐标不变),得到函数的图象.(1)、求的解析式;(2)、求在上的值域;(3)、若在上的图象与直线有且仅有1个公共点,求的取值范围.
-
7、已知函数.(1)、求的单调递减区间;(2)、用“五点法”作出在一个周期内的简图的过程如下,请先补全表格,然后在下图的坐标系中作出在一个周期内的简图.
列表:
画图:

-
8、(1)若 , 求的值;
(2)若 , 是关于的方程的两根,求的值.
-
9、已知函数 .(1)、求的定义域;(2)、求不等式的解集.
-
10、已知函数( , 且)在上单调递增,则的取值范围为.
-
11、敦煌莫高窟飞天壁画折扇的展开图如图1所示,其平面简化图如图2所示,该扇子的扇面(扇环形)可视为扇形截去扇形所剩余的部分.已知 , , , 则该扇子的扇面面积为 .

-
12、已知是奇函数,当时, , 则 .
-
13、已知一正弦电流(单位:A)随时间(单位:s)变化的函数的部分图象如图所示,则( )
 A、 B、 C、 D、在一个周期内,电流不超过30A的时长为
A、 B、 C、 D、在一个周期内,电流不超过30A的时长为 -
14、关于的不等式的解集为的充分不必要条件有( )A、 B、 C、 D、
-
15、已知角的终边上一点的坐标为 , 则( )A、为第四象限角 B、 C、 D、
-
16、若 , , , 则( )A、 B、 C、 D、
-
17、函数的单调递减区间为( )A、 B、 C、 D、
-
18、已知 , 则的最小值为( )A、6 B、12 C、18 D、24
-
19、函数图象的对称中心为( )A、 B、 C、 D、
-
20、已知是幂函数,则( )A、 B、 C、1 D、2