相关试卷
-
1、科学家经过测量发现候鸟的飞行速度可以表示为函数 , 单位是 , 其中表示候鸟每分钟耗氧量的单位数,表示测量过程中候鸟每分钟的耗氧偏差.()(1)、若 , 候鸟每分钟的耗氧量为8100个单位时,它的飞行速度是多少?(2)、若雄性候鸟的飞行速度为 , 雌性候鸟的飞行速度为 , 那么此时雄性候鸟每分钟的耗氧量是雌性候鸟每分钟的耗氧量的多少倍?
-
2、设函数 , 已知对任意 , 若、满足 , , 则 , 则正实数的最大值为 .
-
3、甲、乙、丙3人做传球游戏,游戏规则为:一人随机将球传到另外两人中的一人手里,接到球的一人再将球随机传到另外两人中的一人手里,如此循环传递下去,如果由甲先传球,则连续传球五次后,球在甲手里的概率为.
-
4、已知由样本数据组成的一个样本,得到回归直线方程为 , 且 , 剔除一个偏离直线较大的异常点后,得到新的回归直线经过点.则下列说法正确的是( )A、相关变量 x,y具有正相关关系 B、剔除该异常点后,样本相关系数的绝对值变大 C、剔除该异常点后的回归直线经过点 D、剔除该异常点后,回归直线的斜率是
-
5、已知函数 , 若为方程的解,则( )A、2 B、3 C、4 D、5
-
6、如图所示
 , 5颗串珠用一根细线串起,现将它们依次取出(只允许从两边取出),一次取一颗,两颗☆☆串珠被连续取出的概率是( ) A、 B、 C、 D、
, 5颗串珠用一根细线串起,现将它们依次取出(只允许从两边取出),一次取一颗,两颗☆☆串珠被连续取出的概率是( ) A、 B、 C、 D、 -
7、函数(为自然常数)的大致图像是( )A、
 B、
B、 C、
C、 D、
D、
-
8、若直线与幂函数的图象依次交于不同的三点 , 则下列说法正确的是( )A、 B、 C、 D、以上说法都不正确
-
9、在的展开式中,系数为整数的项数是( )A、8 B、5 C、3 D、2
-
10、已知函数 .(1)、若 , 求函数的极值点;(2)、讨论的单调性.
-
11、定义:若对 , , 都有(j为常数,且),则称数列为“绝对等差数列”,常数j为数列的“绝对公差”.已知“绝对公差”数列所有项的和为E.(1)、若 , , , 请写出有序实数对的所有取值;(2)、若数列共有259项,且 , , , 求数列的通项公式;(3)、若j为奇数,数列共有2k( , )项,且 , . 证明:k为偶数,并写出一个符合条件的数列 .
-
12、已知双曲线( , )的焦距为 , 右顶点为A,直线l与双曲线E相交于P,Q两点,且与E的一条渐近线相交于点 .(1)、求双曲线E的方程;(2)、是否存在直线l,使得与的面积相等?若存在,求出直线l的方程;若不存在,请说明理由;(3)、若直线AP,AQ分别与y轴相交于M,N两点,证明:为定值.
-
13、已知函数 .(1)、当时,求函数的极值点个数;(2)、若对 , 恒成立,求实数a的取值范围.
-
14、如图,三棱柱中, , , 平面平面 , D为棱的中点, .
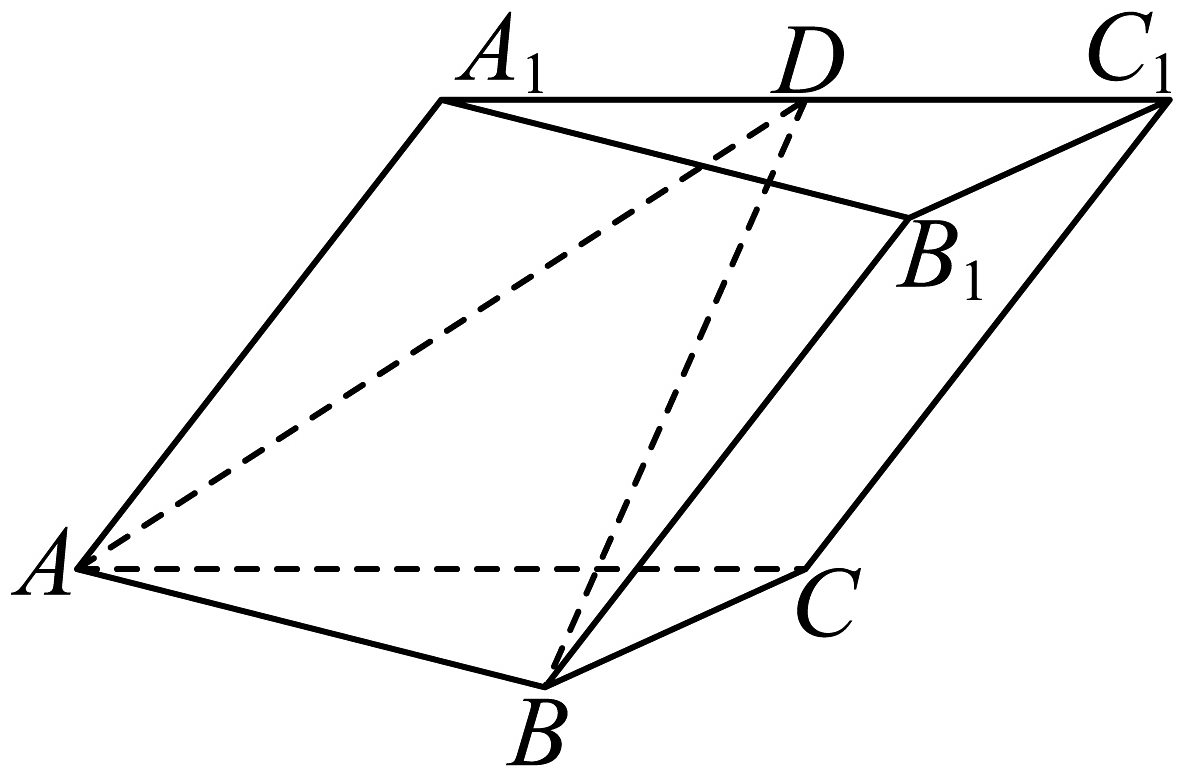 (1)、证明:;(2)、求平面ABD与平面夹角的余弦值.
(1)、证明:;(2)、求平面ABD与平面夹角的余弦值. -
15、固态电池是纯电动汽车搭载的新一代电池,与使用电解液的传统液态锂离子电池相比,固态电池具有安全性能高、能量密度大等特点.某公司试生产了一批新型固态电池,为了了解该批次固态电池的“循环寿命”x(循环寿命是指:电池的容量下降到初始容量的某一阈值时,完成充放电循环的次数)的情况,从这批固态电池中随机抽取了100组进行了测试,并统计绘制了下表:
循环寿命x(千次)
组数y
5
15
a
b
5
已知循环寿命x(千次)的平均值(同一组中的数据用该组区间的中点值代表).
(1)、求a,b的值;(2)、根据测试数据可以认为“循环寿命”x近似服从正态分布 , 经计算样本标准差s的估计值为0.7.用样本数据的平均值作为的值,用样本标准差s的估计值作为的值.(ⅰ)若规定:循环寿命的电池为一等品;的电池为优等品.求试生产的电池的一等品率和优等品率的估计值(结果用百分数表示);
(ⅱ)在该型电池的生产中,称发生概率低于0.27%的事件为小概率事件,在质量控制时,如果小概率事件未发生,则认为该批产品合格;否则可以认为该批产品不合格.若这100组电池中,循环寿命x的最大值和最小值分别为6.5和2.3.请判断该批固态电池是否合格?并说明理由.
参考数据:若随机变量 , 则 , , .
-
16、已知函数的值域为D,集合 , 若 , 则实数a的最大值为 .
-
17、将圆周率的近似值的各个数位上的数字重新排列后得到5位小数M(包括T),则的概率为 .
-
18、已知直线与抛物线相交于A,B两点,D为抛物线的准线与y轴的交点,若的面积为4,则 .
-
19、超椭圆(superellipse)也称为Lamé曲线,是一种类似于椭圆的封闭曲线,保留了椭圆的长轴、短轴、对称性等特点.超椭圆在平面直角坐标系中的方程为( , , ),当 , 时,该超椭圆即为著名的“星形线”,记为曲线C(如图),已知点在曲线C上,O为坐标原点,点为曲线C上任意一点.则下列结论正确的是( )
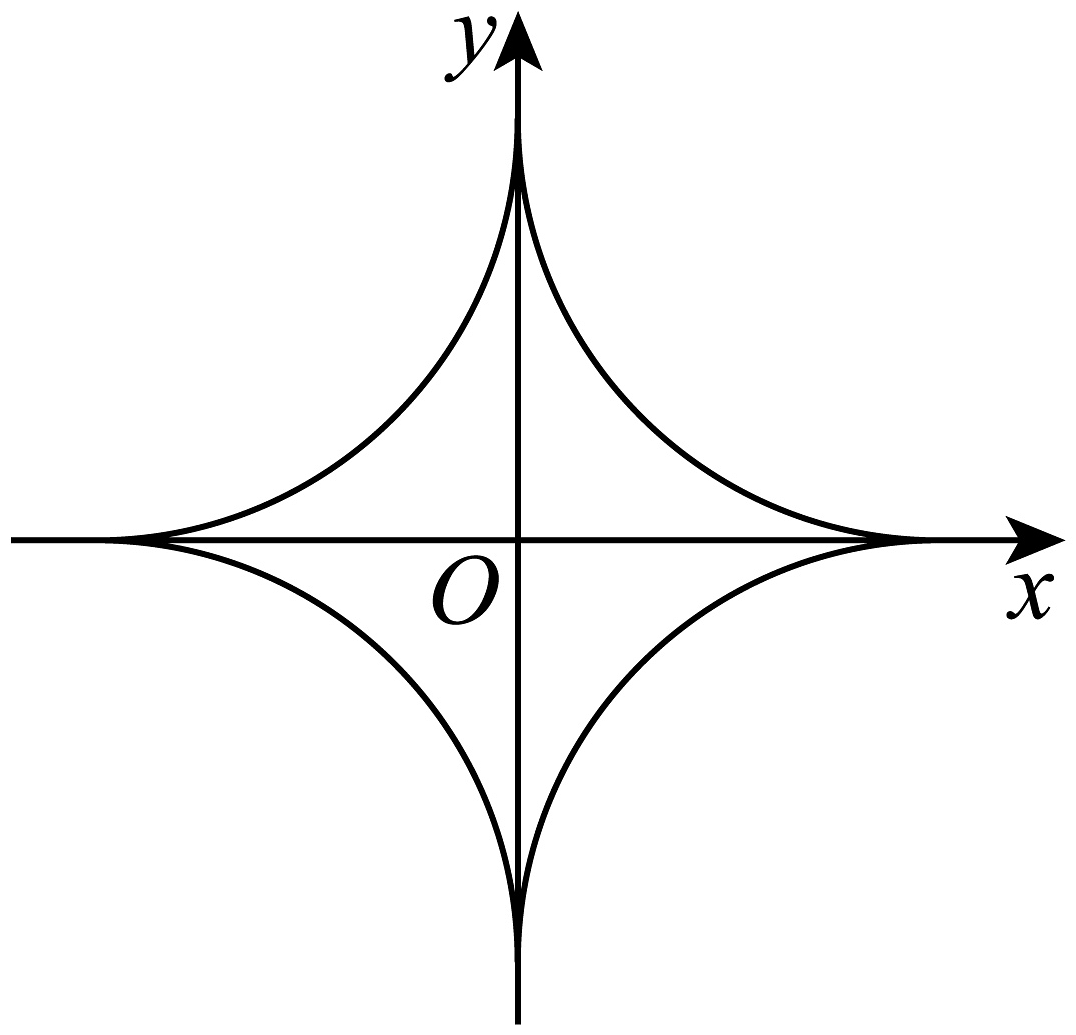 A、 B、的最大值为 C、的最小值为 D、直线与曲线C恰有3个公共点
A、 B、的最大值为 C、的最小值为 D、直线与曲线C恰有3个公共点 -
20、如图,在棱长为4的正方体中,分别为棱 , 底面的对角线上的动点,且 , 则下列结论正确的是( )
 A、三棱锥的体积为 B、平面 C、存在实数 , 使得 D、若直线与平面所成角的正弦值为 , 则
A、三棱锥的体积为 B、平面 C、存在实数 , 使得 D、若直线与平面所成角的正弦值为 , 则