相关试卷
-
1、已知函数 .(1)、若 , 试判断函数在区间内的极值点个数,并说明理由;(2)、当 , 时,求证: . (参考数据:)
-
2、记内角的对边分别为 , 已知 .(1)、求;(2)、若为钝角三角形,求 .
-
3、已知棱长为2的正方体中,为中点,四点都在球的球面上,且四点都在球的球面上,记球与球两球面上的所有公共点构成轨迹 , 则的周长为 .
-
4、在如下的数阵中选出3个数,要求这3个数既不在同一行,也不在同一列.若这3个数的极差不大于5,那么满足条件的选法共有种.
2
5
7
4
9
10
6
8
11
-
5、已知 , 为单位向量,且在上的投影向量为 , 则与的夹角为 .
-
6、已知集合 , 则称集合为分集.下列说法正确的是( )A、当时,是唯一的分集 B、对任意 , 总存在至少一个分集 C、若是分集,则 D、若是分集,则
-
7、动圆过定点 , 且与圆相内切于点 , 记圆心的轨迹为曲线 . 则( )A、曲线的方程为: B、动圆面积的最小值为 C、的最大值为3 D、的最小值是
-
8、已知 , , 且满足 , 则最小值为( )A、 B、 C、 D、
-
9、已知抛物线的焦点为 , 纵坐标为的点在上.若以为圆心,为半径的圆被轴截得的弦长为 , 则( )A、 B、2 C、 D、
-
10、已知直线是曲线的一条切线,则( )A、1 B、2 C、 D、
-
11、已知函数 , 则满足的实数的取值范围是( )A、 B、 C、 D、
-
12、为考察某种药物对预防疾病的效果,进行了动物试验,根据120个有放回随机样本的数据,得到如下列联表:
药物
疗效
合计
未患疾病
患疾病
未服用
10
50
60
服用
18
42
60
合计
28
92
120
经计算得到 , 根据小概率值的独立性检验(已知独立性检验中),结论为( )
A、药物对预防疾病没有效果 B、药物对预防疾病没有效果,这种判断犯错误的概率不超过 C、药物对预防疾病有效果 D、药物对预防疾病有效果,这种判断犯错误的概率不超过 -
13、已知空间中两条直线 , 及平面 , 且满足 , “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分又不必要条件
-
14、已知复数 , 则( )A、 B、2 C、 D、5
-
15、已知椭圆的右焦点为 , 则的长轴长为( )A、 B、 C、 D、
-
16、已知为等比数列的前项和,若 , 则( )A、5 B、9 C、 D、
-
17、已知圆锥的母线长为 , 其外接球体积为 , 则该圆锥的表面积为( )A、3π B、6π C、9π D、12π
-
18、如图,在△ABC中, , P是线段BN上的一点,若 , 则实数m等于( )
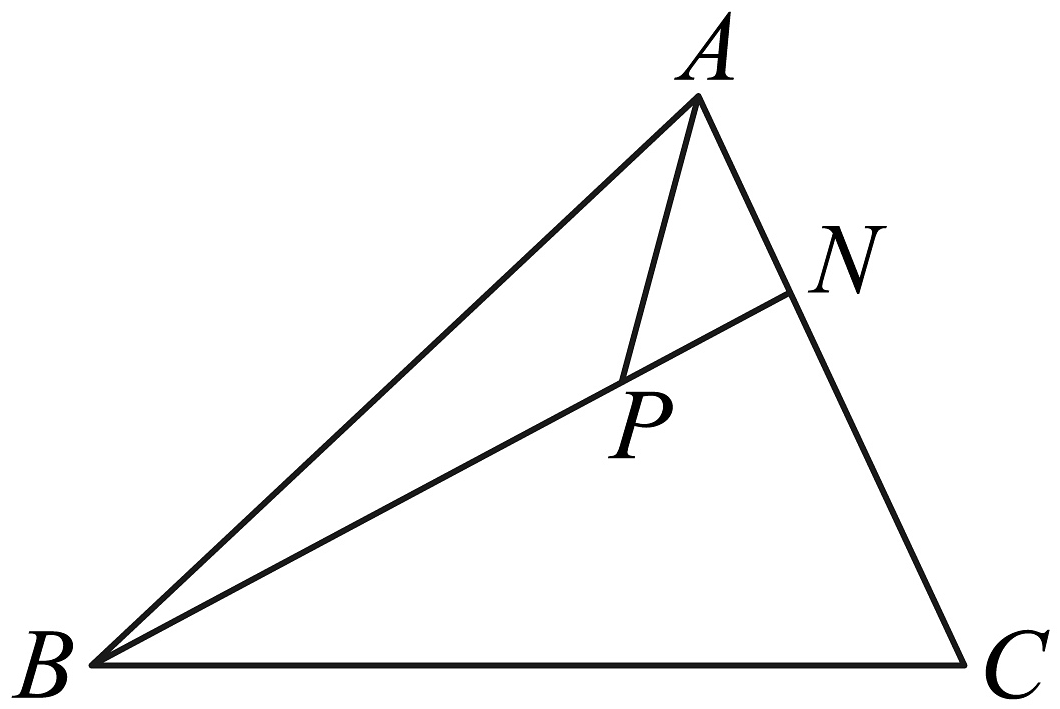 A、 B、 C、 D、
A、 B、 C、 D、 -
19、某封闭的圆锥容器的轴截面为等边三角形,高为6.一个半径为1的小球在该容器内自由运动,则小球能接触到的圆锥容器内壁的最大面积为 .
-
20、设函数 , 若且 , 则的取值范围是 .