相关试卷
-
1、已知正数满足 , 则的最小值为( )A、8 B、7 C、6 D、5
-
2、在中,角所对的边分别为 , 已知 , 且.(1)、求的值;(2)、求的值.
-
3、现有一种不断分裂的细胞,每个时间周期内分裂一次,一个细胞每次分裂能生成一个或两个新的细胞,每次分裂后原细胞消失,设每次分裂成一个新细胞的概率为 , 分裂成两个新细胞的概率为;新细胞在下一个周期内可以继续分裂,每个细胞的分裂相互独立. 设有一个初始的细胞,在第一个周期内开始分裂,记个周期结束后,细胞的数量为 , 其中.(1)、若 , 求的分布列和数学期望;(2)、求;(3)、求证:.
-
4、设函数 , 则下列结论错误的是( )A、的最小正周期为 B、的图象关于直线对称 C、的一个零点为 D、的最大值为1
-
5、如图1,在中, , , 为中点,于 , 延长交于 , 将沿折起,使平面平面 , 如图2所示.
 (1)、平面(2)、求二面角的余弦值;(3)、在线段上是否存在点使得平面?若存在,求的值;若不存在,请说明理由.
(1)、平面(2)、求二面角的余弦值;(3)、在线段上是否存在点使得平面?若存在,求的值;若不存在,请说明理由. -
6、已知数列的首项 , 且满足 .(1)、求数列的通项公式;(2)、记 , 求的前项和 .
-
7、如图,平行六面体的底面是边长为1的正方形,且 , , 则线段的长为( )
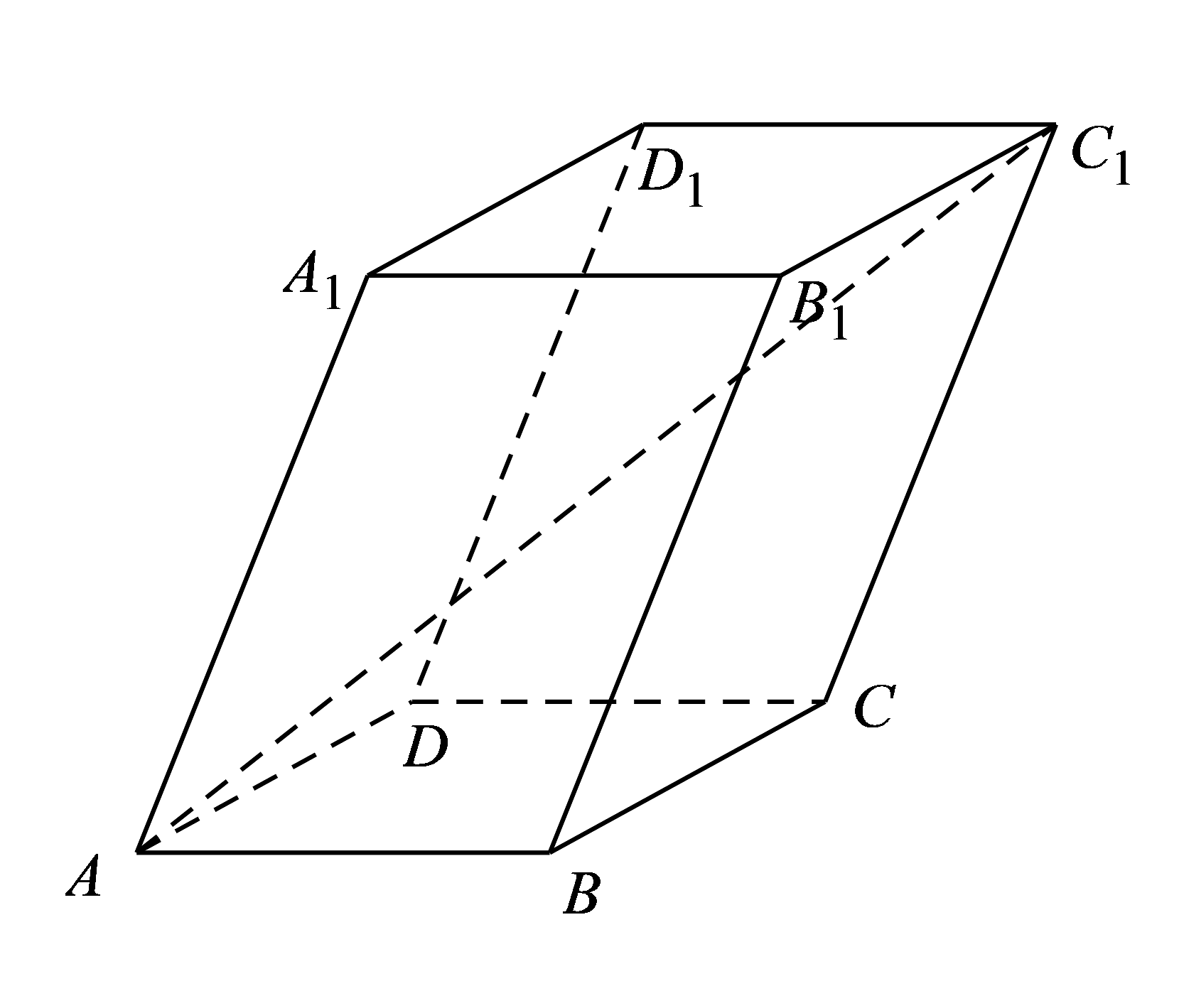 A、 B、 C、 D、
A、 B、 C、 D、 -
8、已知函数 , 若 , 则的取值范围是( )A、 B、 C、 D、
-
9、已知函数的定义域为 , 则函数的定义域为( )A、 B、 C、 D、
-
10、如图所示,椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.已知椭圆的左、右焦点为 , , P为椭圆上不与顶点重合的任一点,I为的内心,记直线OP,PI(O为坐标原点)的斜率分别为 , , 若 , 则椭圆的离心率为 .

-
11、已知空间向量 , , 若 , 则( )A、1 B、-2 C、2 D、
-
12、已知函数是偶函数,当时, , 若函数在区间上具有单调性,则实数a的取值范围是.
-
13、如图,在直三棱柱中,AB⊥AC, , 点E,F分别为棱AB、的中点.
 (1)、求直线与直线AF的夹角的余弦值;(2)、求点F到平面的距离.
(1)、求直线与直线AF的夹角的余弦值;(2)、求点F到平面的距离. -
14、已知数列的前项和满足.
(1)求数列的通项公式;
(2)若 , 求数列的前项和.
-
15、已知是各项均为正数的等比数列,数列满足 .(1)、求数列的通项公式;(2)、求数列的前项和 .
-
16、在中,角的对边分别为 , , , 已知 , .(1)、求角的大小.(2)、若.
(i)求的值.
(ii)求的面积.
-
17、设全集 , 已知集合 , .求和.
-
18、若 , , 则
-
19、若二项式的展开式中常数项为20,则 .
-
20、找规律:1,4,9,16, , 36.