相关试卷
-
1、已知实数、满足方程 , 则下列说法正确的是( )A、直线被圆截得的弦长为 B、的最大值 C、的最大值为 D、的最大值为
-
2、下列说法一定正确的是( )A、过点的直线方程为 B、直线的倾斜角为 C、若 , , 则直线不经过第三象限 D、过、两点的直线方程为
-
3、已知平面与平面平行,若是平面的一个法向量,则平面的法向量可能为( )A、 B、 C、 D、
-
4、已知向量 , 则与的夹角为( )A、 B、 C、 D、
-
5、若椭圆的右焦点坐标是 , 长轴长是 , 则椭圆的标准方程为( )A、 B、 C、 D、
-
6、已知直线的倾斜角为 , 在轴上的截距是 , 则直线的方程为( )A、 B、 C、 D、
-
7、向量 , , 若 , 则( )A、 B、 , C、 , D、 ,
-
8、已知点、 , 则过、两点的直线斜率为( )A、 B、 C、 D、
-
9、如图,在四棱锥中,平面为的中点,点在上,且 , 设点是线段上(含端点)的一动点.
 (1)、求证:平面;(2)、设与平面所成角为 , 求的范围;(3)、若 , 判断直线是否在平面内,说明理由.
(1)、求证:平面;(2)、设与平面所成角为 , 求的范围;(3)、若 , 判断直线是否在平面内,说明理由. -
10、已知双曲线的左、右顶点分别是 , 点在双曲线上,且直线的斜率之积为3.(1)、求双曲线的方程;(2)、过且斜率不为0的直线与双曲线交于两点,为坐标原点,证明为定值,并求出该定值.
-
11、已知圆的圆心在直线上,且过点.(1)、求圆的方程;(2)、已知点是圆上的一点,求的取值范围;(3)、已知直线与圆交于两点,求的最小值.
-
12、已知点是抛物线上一点,点是抛物线的焦点,为上异于的两动点,且 , 则的最小值为.
-
13、一条光线从射出,经过轴反射后,与圆相切,则反射光线所在直线的方程为.(写出一条即可)
-
14、已知直线的方向向量为 , 平面的法向量为 , 且 , 则.
-
15、如图,已知是相互垂直的两条异面直线,直线与直线相交且垂直,垂足为 , 且线段 , 动点分别位于直线上,若直线与所成的角 , 线段的中点为 , 则以下结论正确的有( )
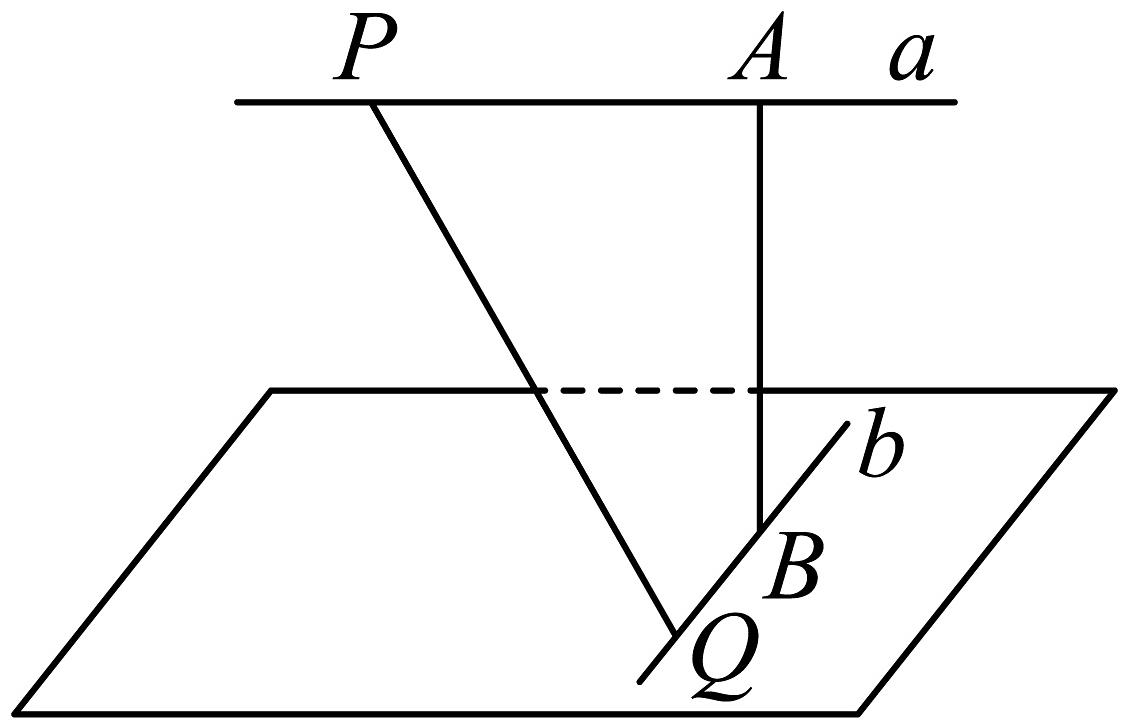 A、的长度为定值4 B、三棱锥的体积为定值 C、点的轨迹是圆 D、直线与所成的角为定值
A、的长度为定值4 B、三棱锥的体积为定值 C、点的轨迹是圆 D、直线与所成的角为定值 -
16、在空间直角坐标系中,点关于平面的对称点为( )A、 B、 C、 D、
-
17、如图所示,在平面直角坐标系中,点绕坐标原点逆时针旋转角至点.
 (1)、试证明点的旋转坐标公式:;(2)、设 , 点绕坐标原点逆时针旋转角至点 , 点再绕坐标原点逆时针旋转角至点 , 且直线的斜率 , 求角的值;(3)、试证明方程为的曲线是双曲线,并求其焦点坐标.
(1)、试证明点的旋转坐标公式:;(2)、设 , 点绕坐标原点逆时针旋转角至点 , 点再绕坐标原点逆时针旋转角至点 , 且直线的斜率 , 求角的值;(3)、试证明方程为的曲线是双曲线,并求其焦点坐标. -
18、已知双曲线的渐近线方程为 , 过右焦点且斜率为的直线与相交于、两点. 点关于轴的对称点为点.(1)、求双曲线的方程:(2)、求证:直线恒过定点,并求出定点的坐标;(3)、当时,求面积的最大值.
-
19、如图,在斜三棱柱中,是边长为2的等边三角形,侧面为菱形,.
 (1)、求证:;(2)、若为侧棱上(包含端点)一动点,求直线与平面所成角的正弦值的取值范围.
(1)、求证:;(2)、若为侧棱上(包含端点)一动点,求直线与平面所成角的正弦值的取值范围. -
20、已知点、的坐标分别为、直线、相交于点 , 且它们的斜率之积是(1)、求点的轨迹方程;(2)、若直线与点的轨迹交于两点,且 , 其中点是坐标原点. 试判断点到直线的距离是否为定值. 若是,请求出该定值;若不是,请说明理由.