相关试卷
-
1、已知等比数列的前n项和为 , 且 , 若 , , 则( )A、550 B、520 C、450 D、425
-
2、已知圆过点 , , 且圆心在直线上.(1)、求圆的方程;(2)、设点在圆上运动,点 , 记为过 , 两点的弦的中点,求的轨迹方程;(3)、在(2)的条件下,若直线与直线交于点 , 证明:恒为定值.
-
3、如图,在长方体中, , , 点E在棱AB上移动.
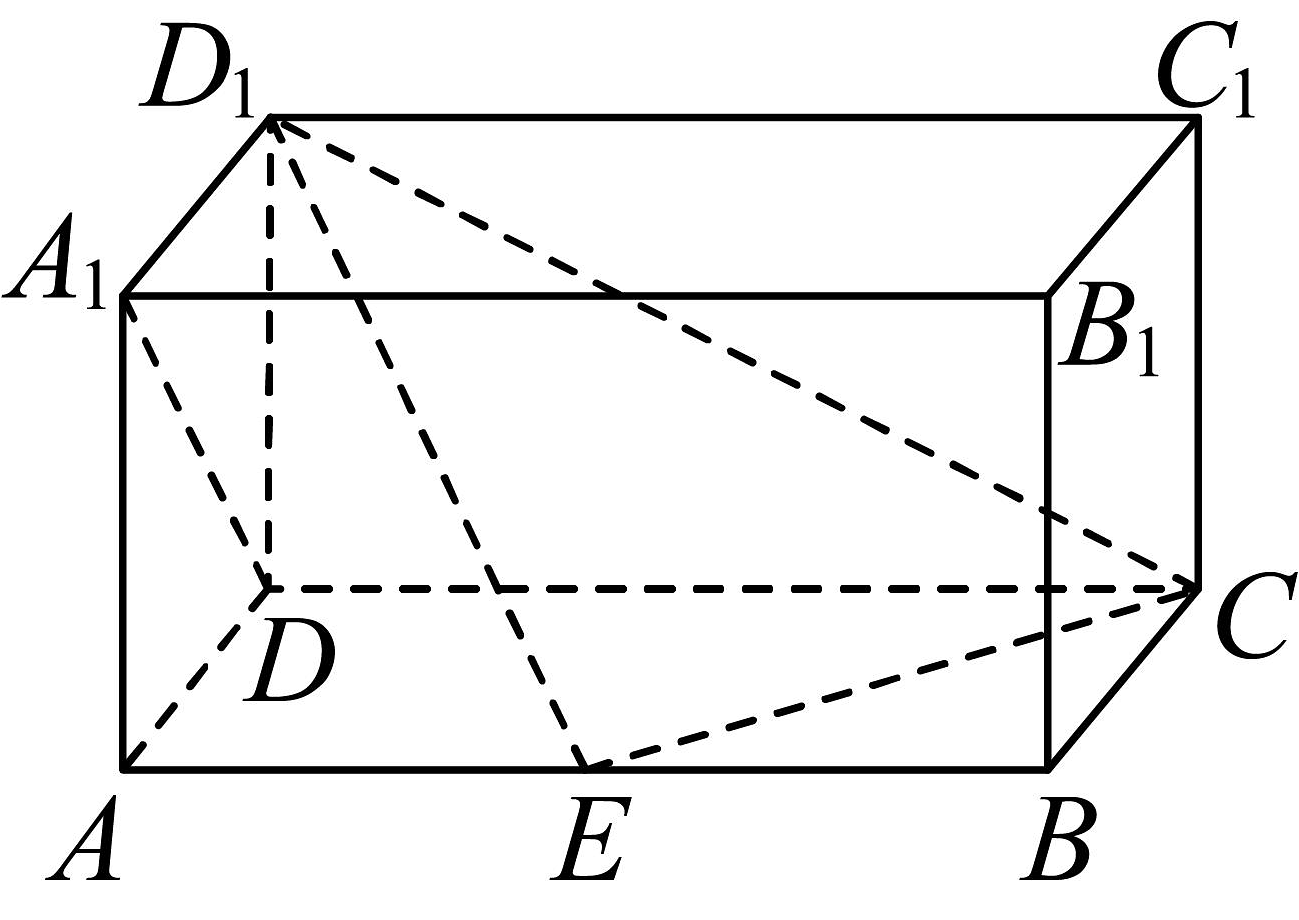 (1)、求证:;(2)、当点E为棱AB的中点时,求点B1到平面ECD1的距离;(3)、当AE为何值时,平面D1EC与平面AECD所成角为?
(1)、求证:;(2)、当点E为棱AB的中点时,求点B1到平面ECD1的距离;(3)、当AE为何值时,平面D1EC与平面AECD所成角为? -
4、如图所示,四棱锥的底面是矩形,底面 , , , , .
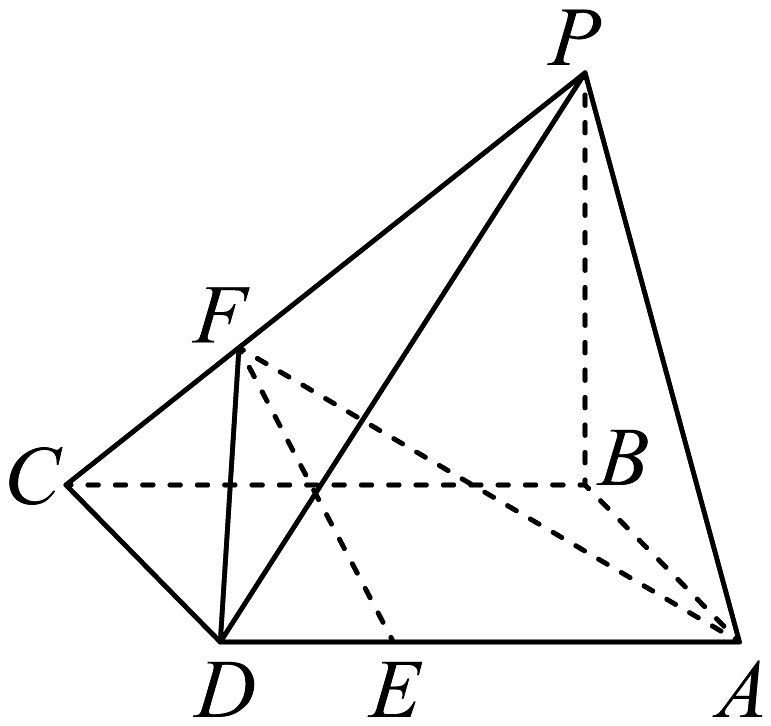 (1)、证明:平面;(2)、求异面直线与所成角的余弦值.
(1)、证明:平面;(2)、求异面直线与所成角的余弦值. -
5、直线与间的距离为3,则.
-
6、点到直线的距离为.
-
7、在正方体中,分别是棱上的动点,且 , 当、共面时,直线和平面夹角的正弦值为( )
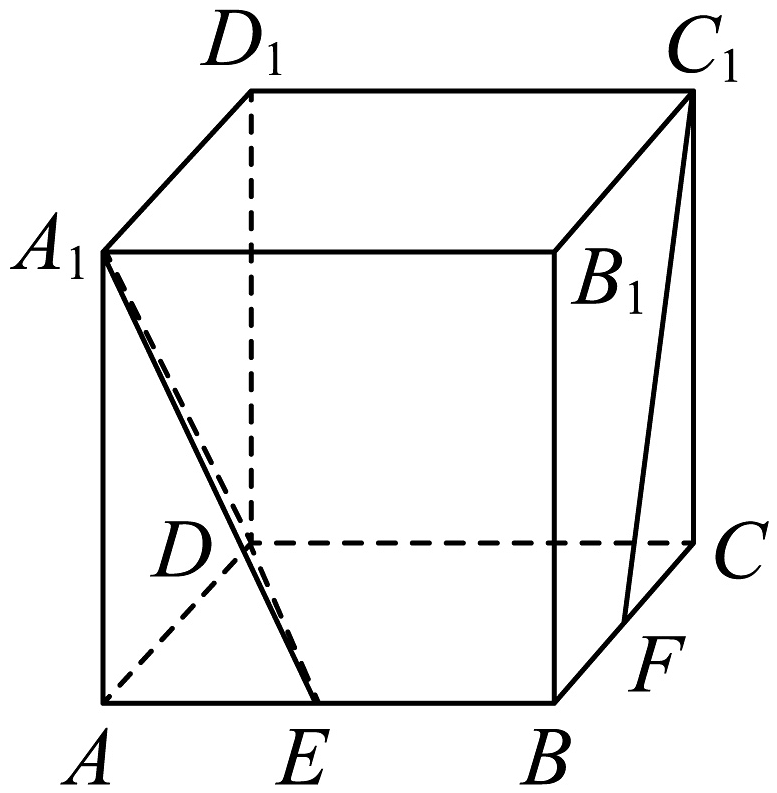 A、 B、 C、 D、
A、 B、 C、 D、 -
8、人教A版选择性必修二教材的封面图案是斐波那契螺旋线,它被誉为自然界最完美的“黄金螺旋”,自然界存在很多斐波那契螺旋线的图案,例如向日葵、鹦鹉螺等.斐波那契螺旋线的画法是:以斐波那契数1,1,2,3,5,8,…为边长的正方形拼成长方形,然后在每个正方形中画一个圆心角为90°的圆弧,这些圆弧所连起来的弧线就是斐波那契螺旋线.下图为该螺旋线在正方形边长为1,1,2,3,5,8的部分,如图建立平面直角坐标系(规定小方格的边长为1),则接下来的一段圆弧所在圆的方程为( ).
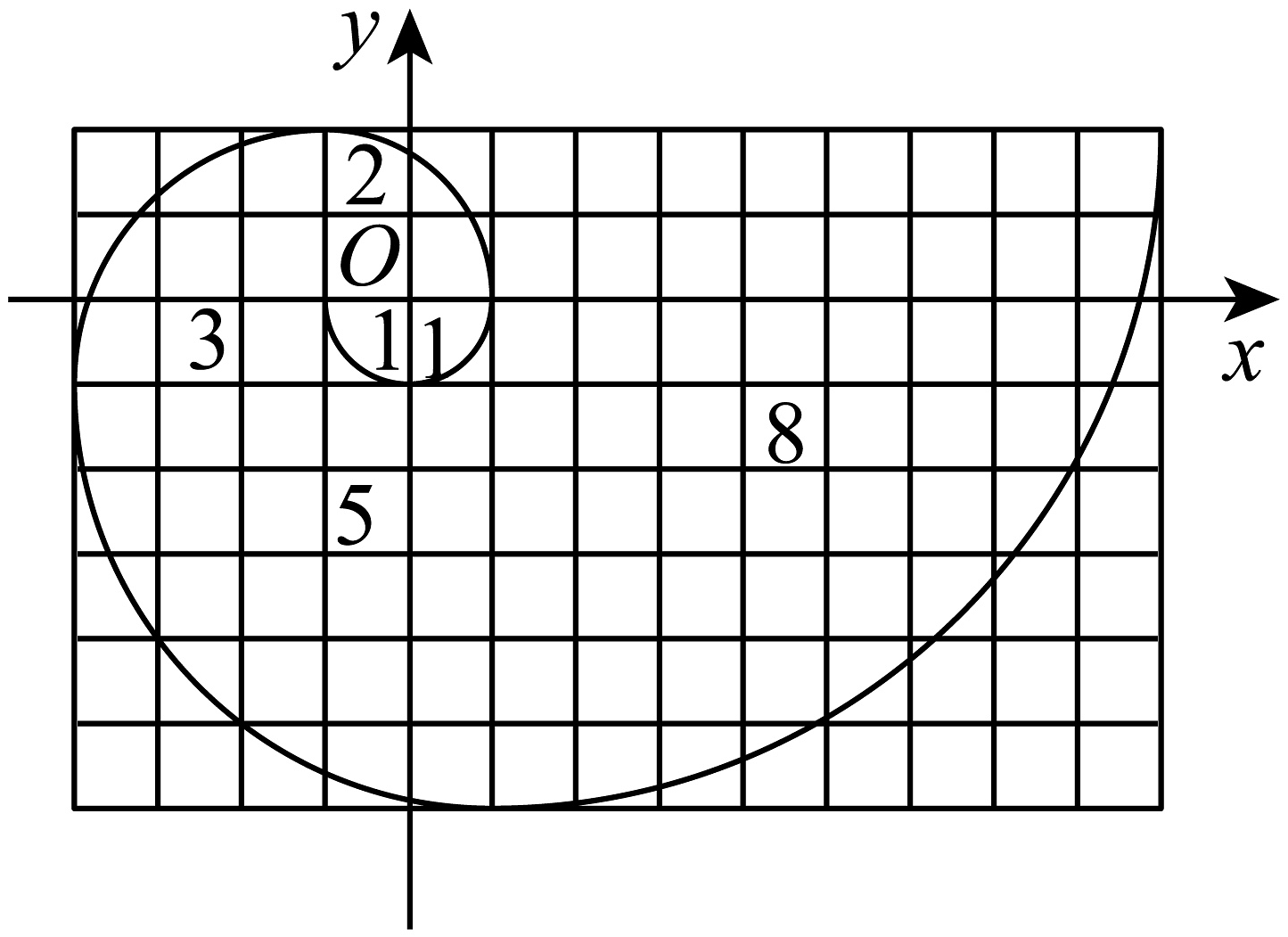 A、 B、 C、 D、
A、 B、 C、 D、 -
9、直线被圆截得的弦长为( )A、2 B、 C、4 D、
-
10、已知函数的定义域为 , 则函数的定义域为( )A、 B、 C、 D、
-
11、已知函数的最小值为.(1)、求的值;(2)、求在上的单调递增区间;(3)、若 , 求的值.
-
12、已知集合 , 则( )A、 B、 C、 D、
-
13、在数列 , 中, , , 且为正项等比数列.(1)、求的通项公式;(2)、证明: .
-
14、已知数列、满足 , , , .(1)、证明:数列为等差数列,并求数列的通项公式;(2)、记数列的前项和为 , 求 , 并证明:.
-
15、已知正项数列前n项和为 , 且满足.(1)、求数列的通项公式;(2)、若数列满足 , 求数列的前项和.
-
16、某部门为了对该城市共享单车加强监督管理,随机调查了1000名用户.根据这1000名用户对某品牌共享单车的评分(满分:100分),绘制出了如图所示的频率分布直方图,其中样本数据分组为
 (1)、试估计这1000名用户评分的平均分;(2)、若采用分层随机抽样的方法从评分在内的用户中抽取5人进行调查,并从这5人中随机选取2人作为记录员,求选取的2名记录员中至少有1人的评分在内的概率.
(1)、试估计这1000名用户评分的平均分;(2)、若采用分层随机抽样的方法从评分在内的用户中抽取5人进行调查,并从这5人中随机选取2人作为记录员,求选取的2名记录员中至少有1人的评分在内的概率. -
17、正项数列满足 , .(1)、证明:数列为等比数列;(2)、求数列的前n项和 .
-
18、数列中,若 , , 则 .
-
19、已知数列中, , 则( )A、 B、 C、 D、
-
20、如图所示的几何体出现在南宋数学家杨辉所著的《详解九章算法·商功》中,后人称为“三角垛”.“三角垛”最上层有1个球,第二层有3个球,第三层有6个球,…,设第层有个球,从上往下层球的总数为 , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、