相关试卷
-
1、如图,在矩形ABCD中, , , 沿矩形对角线BD将折起形成四面体ABCD,在这个过程中,下列结论正确的是( )
 A、在四面体ABCD中,当时, B、四面体ABCD的体积的最大值为 C、在四面体ABCD中,BC与平面ABD所成的角可能为 D、四面体ABCD的外接球的半径为定值
A、在四面体ABCD中,当时, B、四面体ABCD的体积的最大值为 C、在四面体ABCD中,BC与平面ABD所成的角可能为 D、四面体ABCD的外接球的半径为定值 -
2、某电视台的夏日水上闯关节目一共有三关,第一关与第二关的过关率分别为 , , 只有通过前一关才能进入下一关,每一关都有两次闯关机会,且通过每关相互独立.一选手参加该节目,则下列结论正确的是( )A、该选手闯过第一关的概率为 B、该选手单独闯过第二关的概率为 C、该选手能进入第三关的概率为 D、该选手能进入第三关的概率为
-
3、在中,内角A,B,C所对的边分别是a,b,c,则( )A、若 , 则 B、若是单位圆的内接三角形,则 C、若 , 则 D、若 , 则是锐角三角形
-
4、在中, , , , 若 , 则等于( )A、7 B、8 C、12 D、13
-
5、在三棱锥中,平面 , , .若 , A,B,C,D四点都在球的表面上,则球的表面积为( )A、 B、 C、 D、
-
6、已知外接圆的圆心为 , 半径为1,点到近的距离分别为 , , .若 , 则( )A、 B、1 C、 D、2
-
7、某湖中有一小岛 , 沿湖有一条正南方向的公路,一辆汽车在公路处测得小岛在南偏西的方向上,汽车行驶2公里到达处后,又测得小岛在南偏西的方向上,如图所示,则小岛到公路的距离为( )
 A、公里 B、公里 C、公里 D、公里
A、公里 B、公里 C、公里 D、公里 -
8、已知为坐标原点, , , , 若为直线OC上一动点,当取最小值时,( )A、 B、 C、 D、
-
9、不透明的口袋中装有50个大小相同的红球、白球和黑球,其中红球有20个,从口袋中摸出一个球,若摸出白球的概率是0.2,则摸出黑球的概率是( )A、0.2 B、0.3 C、0.4 D、0.6
-
10、若棱长为的正方体的内切球的表面积为 , 则( )A、2 B、4 C、 D、
-
11、如图,已知全集 , 集合 , 则图中阴影部分表示的集合是( )
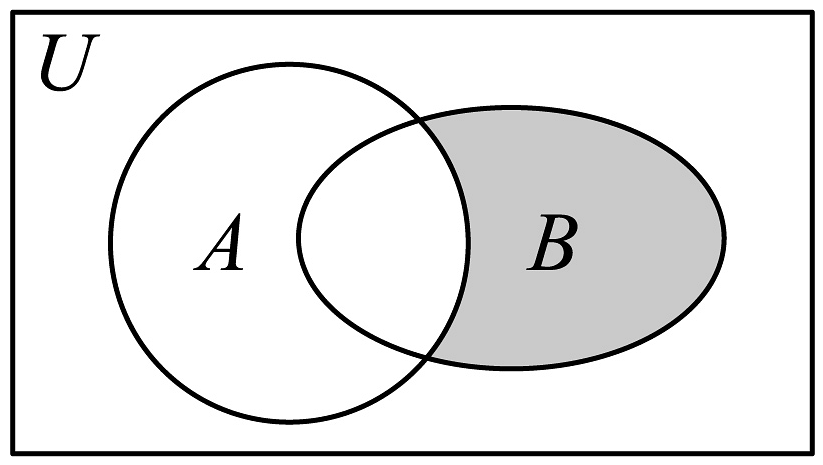 A、 B、 C、 D、
A、 B、 C、 D、 -
12、某学校为了解本校历史、物理方向学生的学业水平模拟测试数学成绩情况,分别从物理方向的学生中随机抽取60人的成绩得到样本甲,从历史方向的学生中随机抽取人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:

已知乙样本中数据在的有10个.
(1)、求和乙样本直方图中的值;(2)、试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的中位数(同一组中的数据用该组区间中点值为代表);(3)、若本校历史方向的学生约为300人,估计其中数学成绩在85分以上的人数. -
13、一个圆锥的侧面展开图是半径为2,圆心角为的扇形,则该圆锥的表面积为 .
-
14、下列说法正确的是( )A、某人在玩掷骰子游戏,掷得数字5的概率是 , 则此人掷6次骰子一定能掷得一次数字5 B、为了了解全国中学生的心理健康情况,应该采用普查的方式 C、一组数据8,8,7,10,6,8,9的众数和中位数都是8 D、若甲组数据的方差 , 乙组数据的方差 , 则乙比甲稳定
-
15、若向量 , 则( )A、 B、2 C、1 D、0
-
16、某校数学兴趣小组的同学对杨辉三角性质进行探究发现:“第n行各数平方和等于第2n行中间的数,即:”,证明如下.证明:考虑多项式中的系数,一方面:代数式中,的系数为.另一方面:代数式中,的系数为.因为 , 所以.所以.(1)、如果证明过程中考虑中的系数,能得到的组合恒等式为________.请先填空,再构造一个实际背景,对所得恒等式的意义作出解释;(2)、证明:①;②.注:组合数 , 若 , 则.
-
17、将函数的图象绕坐标原点逆时针旋转后,所得曲线仍然是一个函数的图象,即函数的图象与直线至多有1个交点,则称函数具有“α旋转不变性”.(1)、证明:函数 , 具有“旋转不变性”;(2)、若函数具有“旋转不变性”,求m的取值范围.
-
18、长时间近距离看电子产品会影响视力.泉泉调查了某校1000名学生,发现40%的学生近视;而该校20%的学生每天近距离看电子产品时间超过1h,这些人的近视率为50%.(1)、请完成下列2×2列联表,并根据小概率值的独立性检验,判断近视与每天近距离看电子产品时间超过1h是否有关联;
近视
每天近距离看电子产品时间超过1h
合计
是
否
是
否
合计
1000
(2)、研究发现,近视儿童每年眼轴的增速要大于非近视儿童,长时间近距离看电子产品会导致眼轴快速增长,最终影响视力.高度近视者的眼轴长度一般大于26mm.下图是每天近距离看电子产品时间超过1h近视儿童和非近视儿童6~16岁的眼轴生长发育散点图.
①根据散点图判断,和哪一个更符合每天近距离看电子产品时间超过1h的近视儿童的眼轴生长发育情况?(给出判断即可,不必说明理由)
②根据①中的判断结果,建立该类近视儿童眼轴长度y(单位:mm)关于年龄x( , 且)的经验回归方程;
③根据②中的结果,估计该类近视儿童开始高度近视时的年龄.(结果保留整数)
参考公式及数据:(ⅰ) , ,
α
0.01
0.005
0.001
6.635
7.879
10.828
(ⅱ)回归方程中斜率和截距的最小二乘估计公式分别为: , ;
(ⅲ)散点图1中 , ;散点图2中 , .
-
19、函数.(1)、当时,求的单调区间;(2)、当时,记在区间上的最大值为M,最小值为m,求的取值范围.
-
20、一个质点从数轴上的原点0开始移动,通过抛掷一枚质地均匀的硬币决定质点向左或者向右移动.若硬币正面向上,则质点向右移动一个单位;若硬币反面向上,则质点向左移动一个单位.抛掷硬币4次后,质点所在位置对应数轴上的数记为随机变量 , 求:(1)、质点位于2的位置的概率;(2)、随机变量的分布列和期望.