相关试卷
-
1、关于空间向量,以下说法正确的是( )A、若 , 则向量 , 的夹角是锐角 B、空间中的三个向量,若有两个向量共线,则这三个向量一定共面 C、若对空间中任意一点O,有 , 则P,A,B,C四点共面 D、若分别表示空间两向量的有向线段所在的直线是异面直线,则这两个向量不共面
-
2、已知直线的一个方向向量为 , 平面的一个法向量为 , 若 , 则( )A、 B、 C、 D、
-
3、在棱长均为1的平行六面体中, , , 则( )A、30° B、45° C、60° D、90°
-
4、已知 , 则在方向上的投影数量为( )A、 B、 C、 D、
-
5、已知 , , , 若、、三个向量共面,则实数A、3 B、5 C、7 D、9
-
6、在空间直角坐标系中,点关于x轴对称的点坐标是( )A、 B、 C、 D、
-
7、函数.(1)、时,讨论的单调性;(2)、若函数有两个极值点、 , 曲线上两点、连线斜率记为 , 求证:.(3)、盒子中有编号为的个小球(除编号外无区别),有放回的随机抽取个小球,记抽取的个小球编号各不相同的概率为 , 求证:.
-
8、已知椭圆的离心率为 , 其左顶点到点的距离为 , 不过原点的直线与椭圆相交于不同的 , 两点,与直线交于点 , 且 , 直线与轴,轴分别交于点 , .(1)、求椭圆的标准方程;(2)、当的面积取最大值时,求的面积.
-
9、如图,在四棱锥中,平面平面 , , , , 为棱的中点.
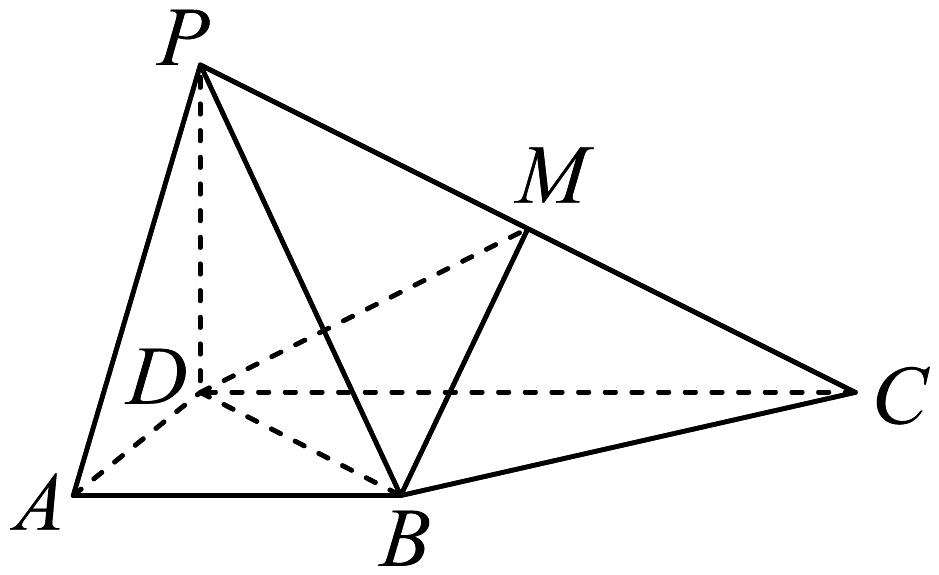 (1)、证明:平面;(2)、若 , ,
(1)、证明:平面;(2)、若 , ,(i)求二面角的余弦值;
(ii)在线段上是否存在点 , 使得点到平面的距离是?若存在,求出的值;若不存在,说明理由.
-
10、已知函数 .(1)、当时,曲线在点()处的切线记为 .
①求的方程;
②设的交点构成 , 试判断的形状(锐角、钝角或直角三角形)并加以证明.
(2)、讨论的极值. -
11、在中,内角的对边分别是 , , .(1)、求角;(2)、若 , 求边上的角平分线长;(3)、若为锐角三角形,求边上的中线的取值范围.
-
12、已知点 , 点F为抛物线的焦点.若以点P,F为焦点的椭圆与抛物线有公共点,则椭圆的离心率的最大值为 .
-
13、在数列中, , 若对于任意的恒成立,则实数k的最小值为.
-
14、随机变量X服从正态分布 , , , 则的最小值为.
-
15、已知圆和圆的交点为 , 则( )A、公共弦所在直线的方程为 B、线段的中垂线方程为 C、公共弦的长为 D、为圆上一动点,则到直线距离的最大值为
-
16、如图,圆锥的底面直径和母线长均为 , 其轴截面为 , 为底面半圆弧上一点,且 , , , 则( )
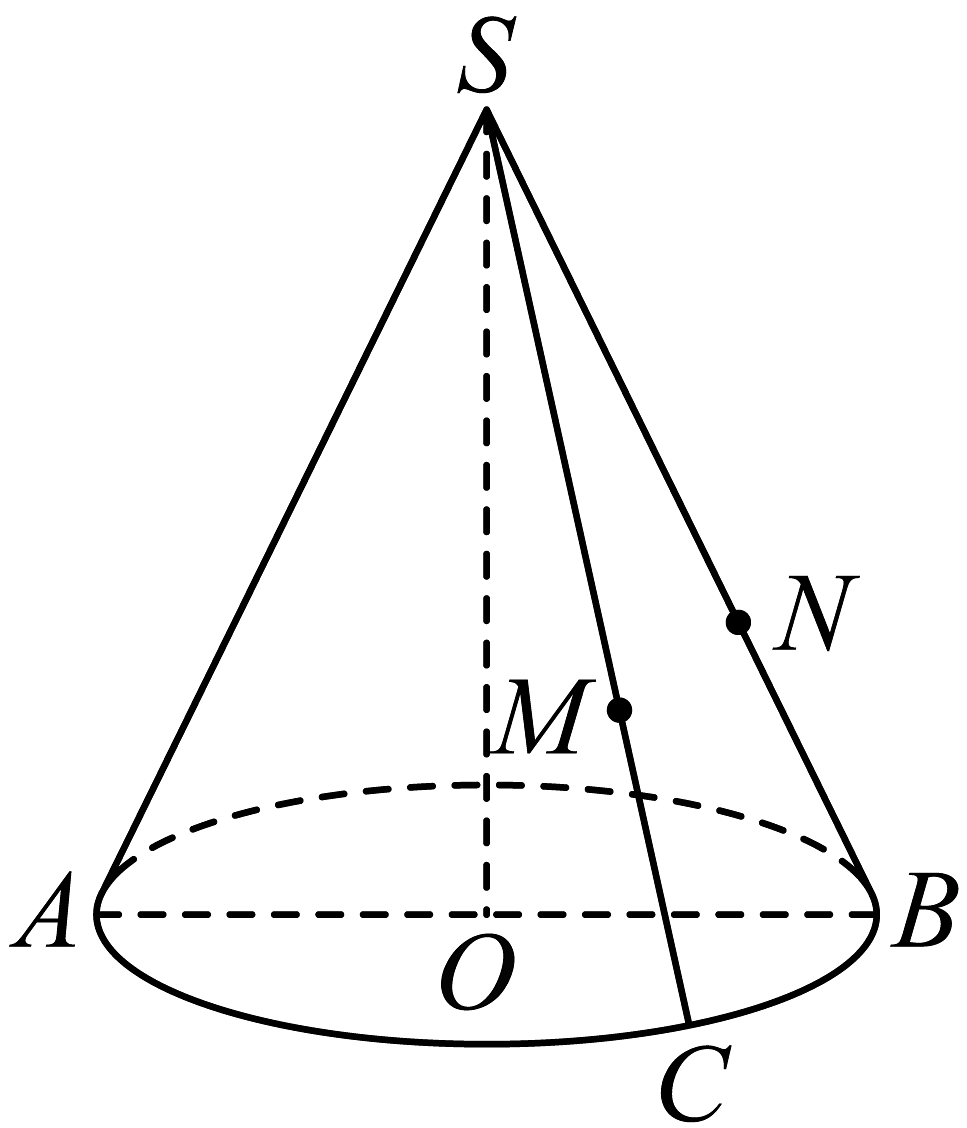 A、存在 , 使得 B、当时,存在 , 使得平面 C、当 , 时,四面体的体积为 D、当时,
A、存在 , 使得 B、当时,存在 , 使得平面 C、当 , 时,四面体的体积为 D、当时, -
17、已知是关于的方程的两根,则( )A、 B、 C、若 , 则 D、若 , 则
-
18、在△中,为的角平分线(在线段上), , 当取最小值时,( ).A、 B、 C、 D、
-
19、已知函数定义域为 , , , , 且 , , 则实数的取值范围是( )A、 B、 C、 D、
-
20、已知点、是椭圆的左、右焦点,点M为椭圆B上一点,点关于的角平分线的对称点N也在椭圆B上,若 , 则椭圆B的离心率为( )A、 B、 C、 D、