相关试卷
-
1、随机变量X服从正态分布 , , , 则的最小值为.
-
2、已知圆和圆的交点为 , 则( )A、公共弦所在直线的方程为 B、线段的中垂线方程为 C、公共弦的长为 D、为圆上一动点,则到直线距离的最大值为
-
3、如图,圆锥的底面直径和母线长均为 , 其轴截面为 , 为底面半圆弧上一点,且 , , , 则( )
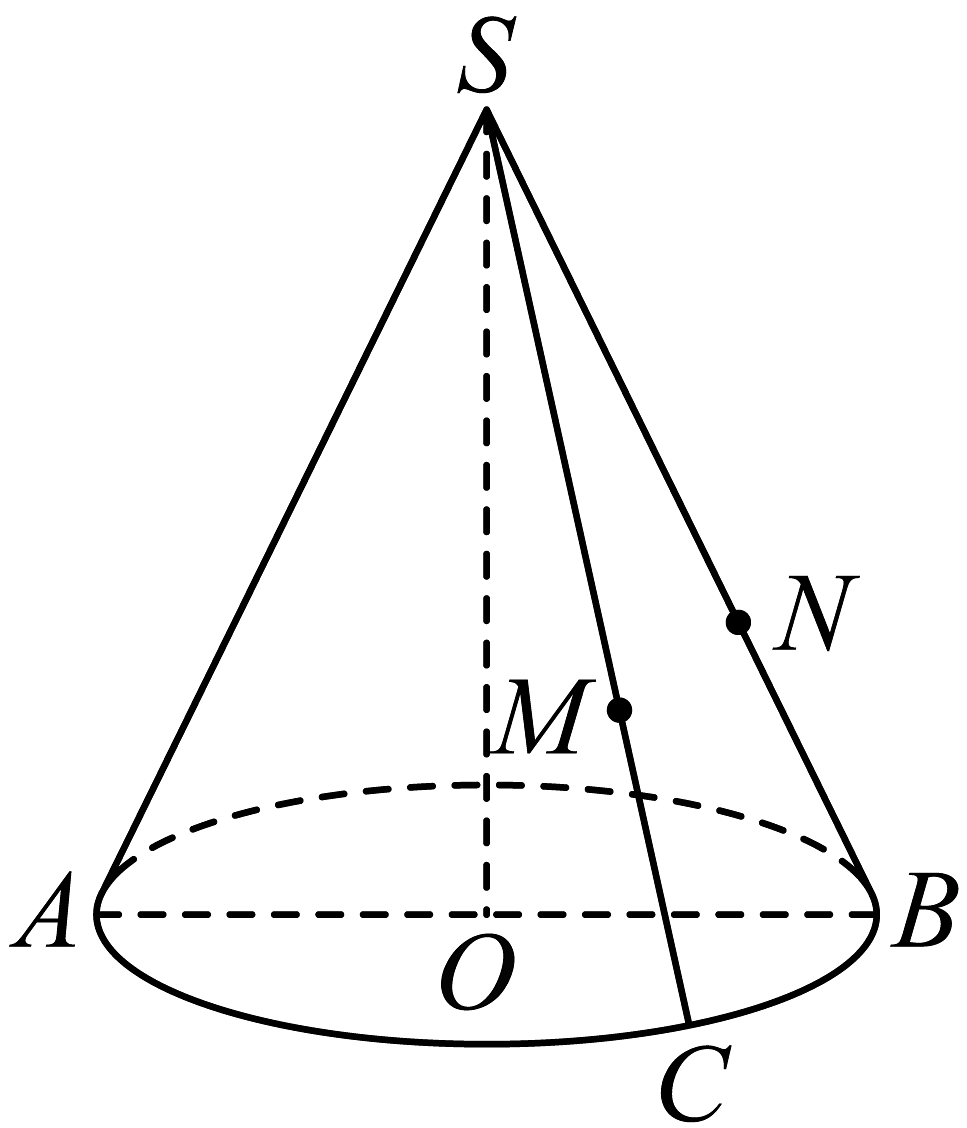 A、存在 , 使得 B、当时,存在 , 使得平面 C、当 , 时,四面体的体积为 D、当时,
A、存在 , 使得 B、当时,存在 , 使得平面 C、当 , 时,四面体的体积为 D、当时, -
4、已知是关于的方程的两根,则( )A、 B、 C、若 , 则 D、若 , 则
-
5、在△中,为的角平分线(在线段上), , 当取最小值时,( ).A、 B、 C、 D、
-
6、已知函数定义域为 , , , , 且 , , 则实数的取值范围是( )A、 B、 C、 D、
-
7、已知点、是椭圆的左、右焦点,点M为椭圆B上一点,点关于的角平分线的对称点N也在椭圆B上,若 , 则椭圆B的离心率为( )A、 B、 C、 D、
-
8、函数图象的一条对称轴为直线 , 则( )A、 B、 C、 D、
-
9、正项递增等比数列 , 前n项的和为 , 若 , , 则( )A、121 B、364 C、728 D、1093
-
10、在中,点是边上一点,若 , 则的最小值为( )A、 B、 C、 D、1
-
11、设集合 , , 若 , 则的取值范围是( )A、 B、 C、 D、
-
12、定义:对函数和 , , 若对任意 , 且 , 均有 , 则称“函数与具有类性质”.(1)、判断与是否具有类性质,并说明理由;(2)、已知 ,
①若与具有类性质,求的取值范围;
②若与具有类性质,且 , 证明: 对任意 , .
-
13、函数满足:对任意实数 , , 有成立;函数 , , , 且当时,.(1)、求并证明函数为奇函数;(2)、证明:函数在上单调递增;(3)、若关于的不等式恒成立,求的取值范围.
-
14、某市为迎接国庆游客,出台了一系列政策.已知该市最多能容纳游客35万人,每万名游客平均可创造160万元的经济效益.已知该市维持旅游市场的成本分为固定成本和流动成本两部分,其中固定成本为300万元/年,每接待万名游客需要投入的流动成本为(单位:万元),
当游客人数不超过14万人时,;
当游客人数超过14万人时, .
(1)、写出该市旅游净收入(万元)关于游客人数(万人)的函数解析式;(注:旅游净收入旅游收入固定成本流动成本);(2)、当游客人数达到多少万人时,该市的旅游净收入能达到最大? -
15、如图,在三棱柱中,侧面是矩形,侧面是菱形,分别是的中点,且 .
 (1)、求证:平面;(2)、若 , 且是边长为4的正三角形,求三棱锥的体积.
(1)、求证:平面;(2)、若 , 且是边长为4的正三角形,求三棱锥的体积. -
16、已知函数 , 若关于的方程有5个不同的实数根,则的取值范围为․
-
17、已知函数是定义在上的奇函数,且时, , 则.
-
18、直线的倾斜角大小为.
-
19、已知非空集合R,若对 , 都有 , 成立,则称集合是封闭集.下列说法中正确的是( )A、集合是封闭集 B、若集合是封闭集,则也是封闭集 C、若集合 , 为封闭集,且 , 则也是封闭集 D、若集合 , 为封闭集,且 , 则也是封闭集
-
20、下列命题为真命题的是( )A、若 , 则 B、若 , 则 C、若 , 且 , 则 D、若 , 则