相关试卷
-
1、如图,在正三棱柱中, , 分别为的中点,则多面体体积为 .

-
2、已知向量与的夹角为 , 且 , , 则在方向上的投影向量坐标为 .
-
3、如图,正三棱台的上下底面边长分别为3和6,侧棱长为3,则下列结论中正确的有( )
 A、过AC的平面截该三棱台所得截面三角形周长的最小值为 B、棱长为的正四面体可以在该棱台内随意转动 C、直径为的球可以整体放入该三棱台内(含与某面相切) D、该三棱台可以整体放入直径为的球内
A、过AC的平面截该三棱台所得截面三角形周长的最小值为 B、棱长为的正四面体可以在该棱台内随意转动 C、直径为的球可以整体放入该三棱台内(含与某面相切) D、该三棱台可以整体放入直径为的球内 -
4、若是平面内两个不共线的向量,则下列选项中正确的是( )A、平面内存在向量不能表示为“”的形式 B、对于平面内的任意向量 , 有且仅有一个实数对 , 使得使 C、若共线的非零向量满足 , 则存在实数 , 使得 D、若实数满足 , 则
-
5、若 , 则( )A、 B、 C、 D、
-
6、若 , 则实数的值为( )A、3 B、2 C、 D、1
-
7、在平面四边形ABCD中,E,F分别为AD,BC的中点,若 , , 且 , 则( )A、 B、 C、 D、
-
8、已知圆锥的母线长为4,过该圆锥顶点的平面截此圆锥所得截面面积的最大值为8,则该圆锥底面半径的取值集合为( )A、 B、 C、 D、
-
9、唐代是我国古代金银器制造最为成熟与发达的时期.强盛的国力、开放的心态、丝绸之路的畅通,使得唐代对外交往空前频繁.走进陕西历史博物馆珍宝馆,你会看到“东学西渐”和“西风东来”,各类珍宝无不反映出唐人对自我文化的自信.素面高足银杯(如图1)就是其中一件珍藏.银杯主体可以近似看作半球与圆柱的组合体(假设内壁光滑,杯壁厚度可忽略),如图2所示.已知球的半径为 , 酒杯容积为 , 则其内壁表面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、在中,“”是“为等腰三角形”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
11、在中,点是上靠近的三等分点,是上靠近的三等分点,则( )A、 B、 C、 D、
-
12、设为虚数单位,复数z满足 , 则复数的虚部是( )A、 B、 C、 D、3
-
13、已知集合 , 则( )A、 B、 C、 D、
-
14、如图,在五棱锥中,平面平面 , , . 四边形为矩形,且 , , .
 (1)、证明:平面;(2)、若 , 求二面角的余弦值;(3)、求直线与平面所成角的正弦值的最小值.
(1)、证明:平面;(2)、若 , 求二面角的余弦值;(3)、求直线与平面所成角的正弦值的最小值. -
15、设是一个随机试验的两个事件,则( )A、若对立,则一定互斥 B、若 , 则 C、若 , 则相互独立 D、若 , 则一定对立
-
16、已知某平面图形的直观图是如图所示的梯形 , 且 , 则原图形OABC的面积为( )
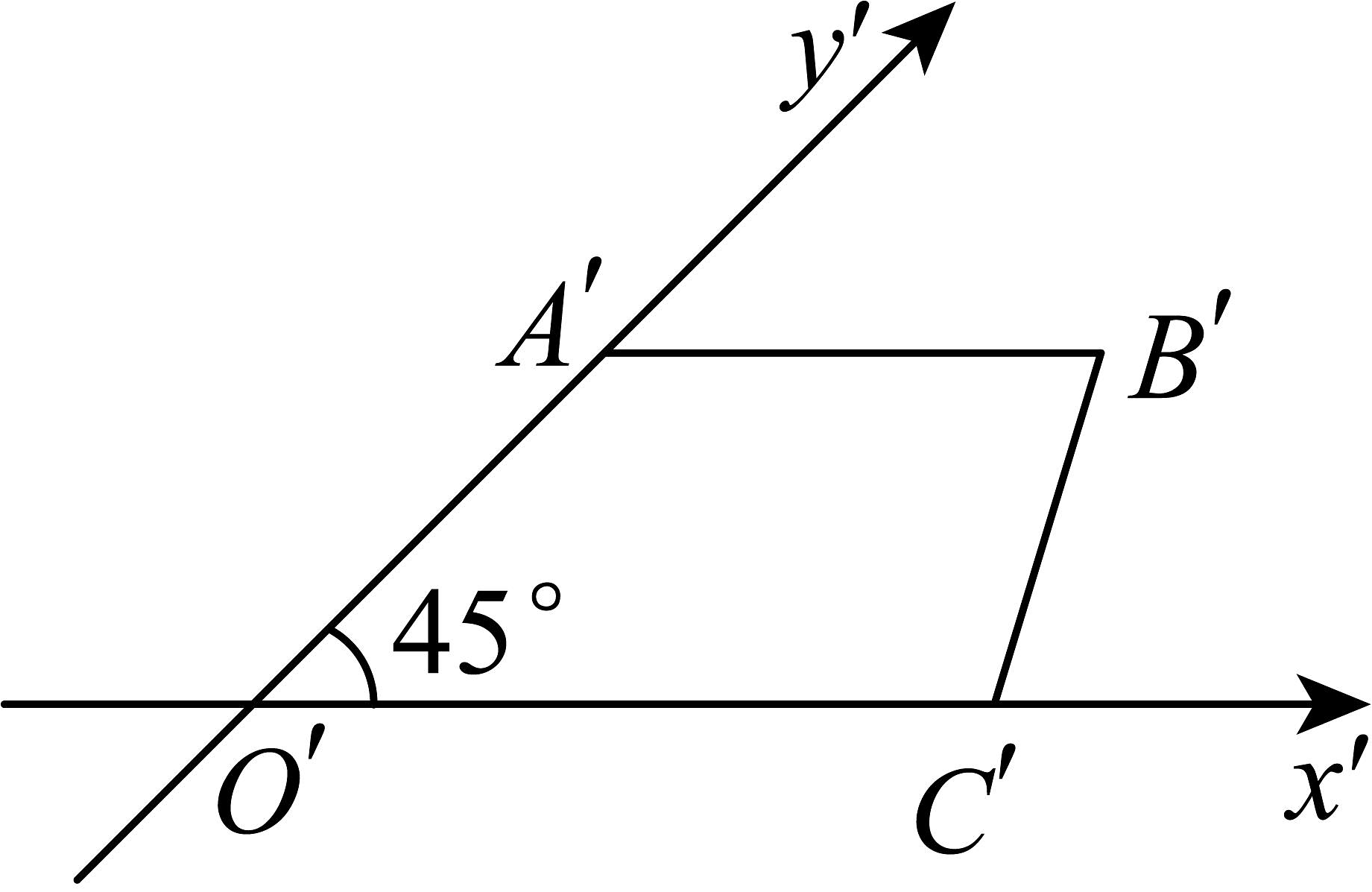 A、 B、 C、12 D、10
A、 B、 C、12 D、10 -
17、二项分布是离散型随机变量重要的概率模型.我们已经知道,若 , 则.多项分布是二项分布的推广,同样是重复次试验,不同的是每次试验的结果不止2种,而有种,记这种结果为事件 , 它们的概率分别为 , 则.现考虑某厂生产的产品分成一等品、二等品、三等品和不合格品 , 它们出现的概率分别为 , 从该厂产品中抽出个,研究各类产品出现的次数的情况,就是一个多项分布.由于产品很多,每次抽取可以看作是独立重复的.(1)、若从该厂产品中抽出4个,且和分别为和0.05,求抽出一等品1个、二等品2个,三等品1个的概率;(2)、现从该厂中抽出个产品,记事件出现的次数为随机变量.为了定出这一多项分布的分布列,只需求出事件的概率,其中为非负整数,.
(i)求;
(ii)对于上述多项分布,求在给定的条件下,随机变量的数学期望.
-
18、已知函数.(1)、若 , 求曲线在点处的切线方程;(2)、求函数在区间上的最大值的表达式;(3)、若函数有两个零点,求实数的取值范围.
-
19、已知分别为三个内角的对边,且.(1)、证明:;(2)、求的最小值.
-
20、如图,在四棱锥中,四边形为正方形,为等边三角形,分别为的中点, , 垂足为.
 (1)、证明:平面;(2)、若 , 求平面与平面形成的锐二面角的余弦值.
(1)、证明:平面;(2)、若 , 求平面与平面形成的锐二面角的余弦值.