版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知圆 $O : x^{2} + y^{2} = 4$ ，弦 $A B$ 过定点 $P (1, 1)$ ，则弦长 $|A B|$ 不可能的取值是（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、4 D、 $2 \sqrt{5}$

查看解析
2、已知 $m, n, l$ 是空间中三条互不重合的直线， $α, β$ 是两个不重合的平面，则下列说法正确的是（）

A、 $m ⊥ α, m ⊥ n$ ，则 $n ∥ α$ B、 $m ∥ n$ 且 $m ⊥ α$ ，则 $n ⊥ α$ C、 $m ∥ α, m ⊥ n$ ，则 $n ⊥ α$ D、 $α ∥ β, l \subset α, n \subset β$ ，则 $l ∥ n$

查看解析
3、已知函数 $f (x) = \frac{3 \cdot 2^{x} - 7}{2^{x} - 3}$ ， $g (x) = |\log_{2} x|$ .
（1）当 $x \in [0, 1]$ 时，求函数 $f (x)$ 的值城
（2）若关于 $x$ 的方程 $g (x) = t$ 有两个不等根 $α, β (α < β)$ ，求 $α β$ 的值；
（3）是否存在实数 $a$ ，使得对任意 $m \in [0 ， 1]$ ，关于 $x$ 的方程 $4 g^{2} (x) - 4 a g (x) + 3 a - 1 - f (m) = 0$ 在区间 $[\frac{1}{8}, 4]$ 上总有3个不等根 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ，若存在，求出实数 $a$ 与 $x_{1} \cdot x_{2} \cdot x_{3}$ 的取值范围；若不存在，说明理由.

查看解析
4、在四棱锥 $P - A B C D$ 中， $B C ∥ A D$ ， $P A ⊥ A D$ ，平面 $P A B ⊥$ 平面 $A B C D$ ， $∠ B A D = 120 °$ ，且 $P A = A B = B C = \frac{1}{2} A D = 2$ .

(1)、求证： $P A ⊥$ 平面 $A B C D$ ；

(2)、求直线 $P B$ 与平面 $P A D$ 所成角的正弦值；

(3)、求二面角 $B - P C - D$ 的余弦值.

查看解析
5、在 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 所对的边长分别为 $a$ ， $b$ ， $c$ ，且满足 $\frac{2 c}{b} = 1 + \frac{\tan A}{\tan B}$ .

(1)、求角 $A$ ；

(2)、角 $A$ 的内角平分线交 $B C$ 于点 $M$ ，若 $a = 4 \sqrt{7}$ ， $A M = 3 \sqrt{3}$ ，求 $\sin ∠ A M C$ .

查看解析
6、函数 $f (x) = 6 {cos}^{2} \frac{ω x}{2} + \sqrt{3} \sin ω x - 3 (ω > 0)$ 在一个周期内的图象如图所示， $A$ 为图象的最高点， $B$ 、 $C$ 为图象与 $x$ 轴的交点，且 $Δ A B C$ 为正三角形.
（1）求 $ω$ 的值及函数 $f (x)$ 的值域；
（2）若 $f (x_{0}) = \frac{8 \sqrt{3}}{5}$ ，且 $x_{0} \in (- \frac{10}{3}, \frac{2}{3})$ ，求 $f (x_{0} + 1)$ 的值.

查看解析
7、某校从参加高一年级期中数学考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段 $[90, 100)$ ， $[100, 110)$ ， $[110, 120)$ ， $[120, 130)$ ， $[130, 140)$ ， $[140, 150]$ ，后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：

(1)、求分数在 $[120, 130)$ 内的频率，并补全这个频率分布直方图；

(2)、估计本次考试的平均分、中位数及 $80 %$ 分位数的值.

查看解析
8、设 $G$ 为 $△ A B C$ 的重心，满足 $\vec{A G} \cdot \vec{B G} = 0$ .若 $\frac{1}{tan A} + \frac{1}{tan B} = \frac{λ}{tan C}$ ，则实数 $λ$ 的值为.

查看解析
9、如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $E, F$ 分别是棱 $A_{1} D_{1}, A_{1} B_{1}$ 的中点， $P$ 是侧面正方形 $B C C_{1} B_{1}$ 内一点（含边界），若 $F P / /$ 平面 $A E C$ ，则线段 $F P$ 长度的取值范围是．

查看解析
10、已知 $α$ 是第三象限角，且 $cos 2 α = - \frac{3}{5}$ ，则 $cos (\frac{π}{2} + α) =$ ， $tan (\frac{π}{4} + 2 α) =$ .

查看解析
11、已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为2，点 $P$ 为平面 $A B C D$ 内一动点，则下列说法正确的是（）

A、若点 $P$ 在棱 $A D$ 上运动，则 $A_{1} P + P C$ 的最小值为 $2 + 2 \sqrt{2}$ B、若点 $P$ 是棱 $A D$ 的中点，则平面 $P B C_{1}$ 截正方体所得截面的周长为 $2 \sqrt{5} + 3 \sqrt{2}$ C、若点 $P$ 满足 $P D_{1} ⊥ D C_{1}$ ，则动点 $P$ 的轨迹是一条直线 D、若点 $P$ 在直线 $A C$ 上运动，则 $P$ 到棱 $B C_{1}$ 的最小距离为 $\frac{2 \sqrt{2}}{3}$

查看解析
12、如图，BC，DE是半径为1的圆O的两条不同的直径， $\overset{⃑}{B F} = 2 \overset{⃑}{F O}$ ，则（）

A、 $\overset{⃑}{B F} = \frac{1}{3} \overset{⃑}{F C}$ B、 $\overset{⃑}{F D} \cdot \overset{⃑}{F E} = - \frac{8}{9}$ C、 $- 1 < \cos < \overset{⃑}{F D}, \overset{⃑}{F E} > \leq - \frac{4}{5}$ D、满足 $\overset{⃑}{F C} = λ \overset{⃑}{F D} + μ \overset{⃑}{F E}$ 的实数 $λ$ 与 $μ$ 的和为定值4

查看解析
13、若正数 $a, b$ 满足 $\frac{1}{a} + \frac{1}{b} = 1$ ，则 $\frac{1}{a - 1} + \frac{4}{b - 1}$ 的最小值为（）

A、4 B、6 C、9 D、16

查看解析
14、若 $\frac{\sin α + \cos α}{\sin α - \cos α} = 2$ ，则 $\sin (α - 5 π) \cdot \sin (\frac{3}{2} π - α)$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{3}{10}$ C、 $\pm \frac{3}{10}$ D、 $- \frac{3}{10}$

查看解析
15、如图，正三角形 $A B C$ 的边长为1，它是水平放置的一个平面图形的直观图，则原图形面积是（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{6}}{2}$ D、 $\frac{\sqrt{6}}{4}$

查看解析
16、已知复数 $z = \frac{2 - i}{1 + i}$ ，则复数 $z$ 的虚部为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{2} i$ C、 $- \frac{3}{2}$ D、 $- \frac{3}{2} i$

查看解析
17、设 $\vec{a}, \vec{b}$ 均为单位向量，且 $\vec{a} \cdot \vec{b} = \frac{1}{4}$ ，则 $|\vec{a} + 2 \vec{b}| =$ （）

A、 $3$ B、 $\sqrt{6}$ C、 $6$ D、 $9$

查看解析
18、已知函数 $f (x) = \frac{1}{x} - x + 2 a \ln x$ （其中 $a$ 是实数）.
（1）若 $a = \frac{1}{2}$ ，求曲线 $y = f (x)$ 在 $(1, f (1))$ 处的切线方程；
（2）求函数 $f (x)$ 的单调区间；
（3）设 $g (x) = \ln x - b x - c x^{2}$ ，若函数 $f (x)$ 的两个极值点 $x_{1}, x_{2} (x_{1} < x_{2})$ 恰为函数 $g (x)$ 的两个零点，且 $y = (x_{1} - x_{2}) g^{'} (\frac{x_{1} + x_{2}}{2})$ 的范围是 $[\ln 2 - \frac{2}{3}, + \infty)$ ，求实数 $a$ 的取值范围.

查看解析
19、放行准点率是衡量机场运行效率和服务质量的重要指标之一.某机场自2012年起采取相关策略优化各个服务环节，运行效率不断提升.以下是根据近10年年份数 $x_{i}$ 与该机场飞往A地航班放行准点率 $y_{i}$ （ $i = 1 ， 2 ， \dots ， 10$ ）（单位：百分比）的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
$\bar{x}$
$\bar{y}$
$\bar{t}$
$\sum_{i = 1}^{10} x_{i}^{2}$
$\sum_{i = 1}^{10} x_{i} y_{i}$
$\sum_{i = 1}^{10} t_{i}^{2}$
$\sum_{i = 1}^{10} t_{i} y_{i}$
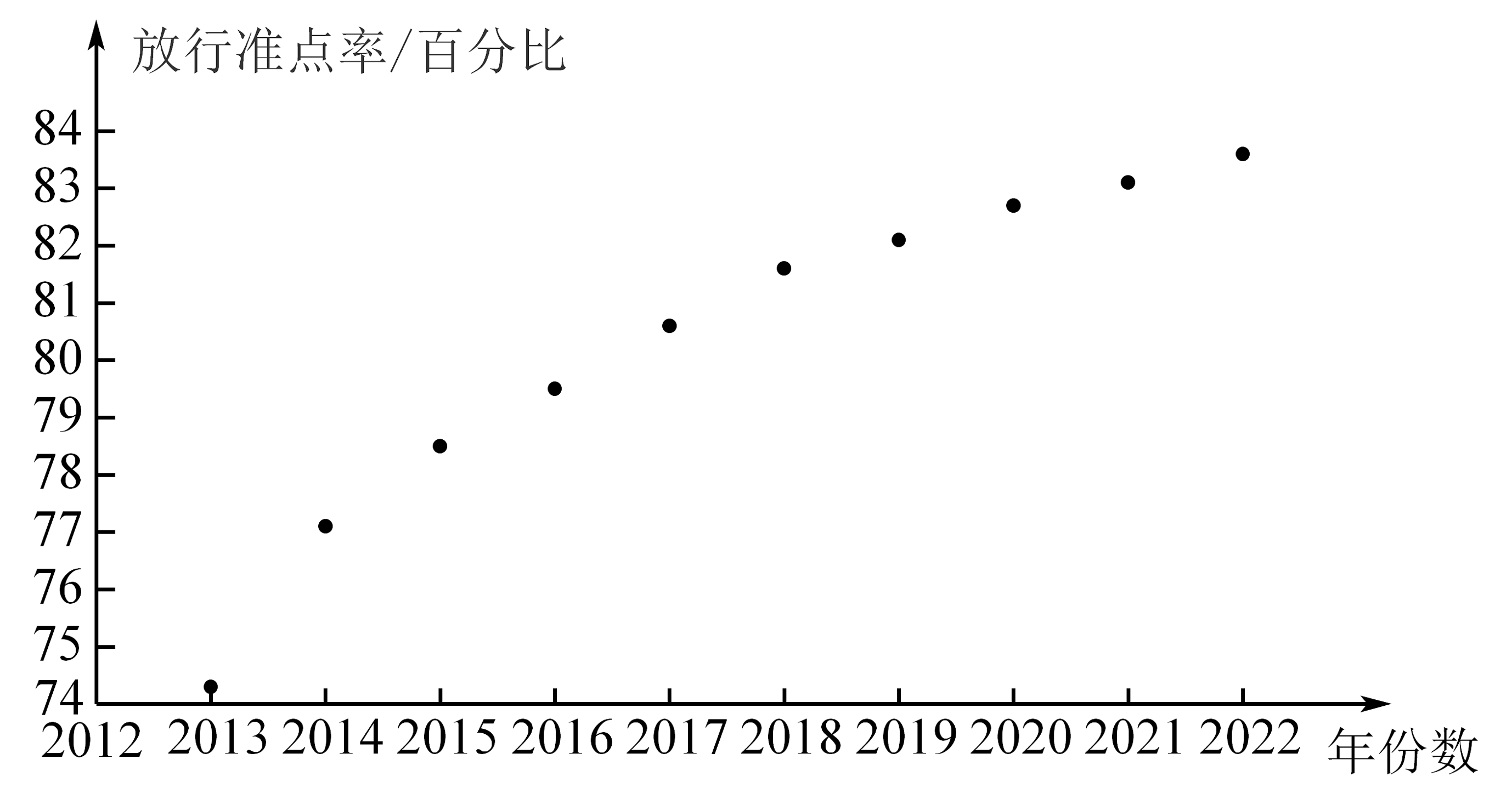
2017.5
80.4
1.5
40703145.0
1621254.2
27.7
1226.8
其中 $t_{i} = \ln (x_{i} - 2012)$ ， $\bar{t} = \frac{1}{10} \sum_{i = 1}^{10} t_{i}$

(1)、根据散点图判断， $y = b x + a$ 与 $y = c \ln (x - 2012) + d$ 哪一个适宜作为该机场飞往A地航班放行准点率y关于年份数x的经验回归方程类型（给出判断即可，不必说明理由），并根据表中数据建立经验回归方程，由此预测2023年该机场飞往A地的航班放行准点率.

(2)、已知2023年该机场飞往A地､B地和其他地区的航班比例分别为0.2、0.2和0.6.若以（1）中的预测值作为2023年该机场飞往A地航班放行准点率的估计值，且2023年该机场飞往B地及其他地区（不包含A、B两地）航班放行准点率的估计值分别为 $80 %$ 和 $75 %$ ，试解决以下问题：
（i）现从2023年在该机场起飞的航班中随机抽取一个，求该航班准点放行的概率；
（ii）若2023年某航班在该机场准点放行，判断该航班飞往A地、B地、其他地区等三种情况中的哪种情况的可能性最大，说明你的理由.
附：（1）对于一组数据 $(u_{1}, v_{1})$ ， $(u_{2}, v_{2})$ ， …， $(u_{n}, v_{n})$ ，其回归直线 $v = α + β u$ 的斜率和截距的最小二乘估计分别为 $\hat{β} = \frac{\sum_{i = 1}^{n} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(u_{i} - \bar{u})}^{2}} = \frac{\sum_{i = 1}^{n} u_{i} v_{i} - n \bar{u} \cdot \bar{v}}{\sum_{i = 1}^{n} u_{i}^{2} - n {\bar{u}}^{2}}$ ， $\hat{α} = \bar{v} - \hat{β} \bar{u}$
参考数据： $\ln 10 \approx 2.30$ ， $\ln 11 \approx 2.40$ ， $\ln 12 \approx 2.48$ .

查看解析
20、已知 $f (x) = {(2 x - 3)}^{n}$ 展开式的二项式系数和为512，且 ${(2 x - 3)}^{n} = a_{0} + a_{1} (x - 1) + a_{2} {(x - 1)}^{2} + \dots + a_{n} {(x - 1)}^{n}$ .

(1)、求 $a_{3}$ 的值；

(2)、求 $a_{1} + a_{2} + a_{3} + \dots + a_{n}$ 的值；

(3)、求 $f (6) - 6$ 被8整除的余数.

查看解析

上一页 1270 1271 1272 1273 1274 下一页跳转

$\bar{x}$	$\bar{y}$	$\bar{t}$	$\sum_{i = 1}^{10} x_{i}^{2}$	$\sum_{i = 1}^{10} x_{i} y_{i}$	$\sum_{i = 1}^{10} t_{i}^{2}$	$\sum_{i = 1}^{10} t_{i} y_{i}$
2017.5	80.4	1.5	40703145.0	1621254.2	27.7	1226.8