相关试卷
-
1、已知曲线 , 则( )A、曲线在第一象限为双曲线的一部分 B、曲线的图象关于原点对称 C、直线与曲线没有交点 D、存在过原点的直线与曲线有三个交点
-
2、关于二项式的展开式,下列说法正确的有( )A、有3项 B、常数项为3 C、所有项的二项式系数和为8 D、所有项的系数和为0
-
3、已知 , 且 , 则的最大值为( )A、9 B、12 C、36 D、48
-
4、已知等比数列的前项和为 , 若恒成立,则的最小值为( )A、 B、 C、 D、1
-
5、若 , 设 , 则a,b,c的大小关系为( )A、 B、 C、 D、
-
6、若将大小形状完全相同的三个红球和三个白球(除颜色外不考虑球的其他区别)排成一排,则有且只有两个白球相邻的排法有( )A、6 B、12 C、18 D、36
-
7、已知直线a,b,c是三条不同的直线,平面α,β,γ是三个不同的平面,下列命题正确的是( )A、若 , 则 B、若 , 则 C、若 , 且 , 则 D、若 , 且 , 则
-
8、在锐角中,角 , , 的对边为 , , , 若 , .
 (1)、求角的大小;(2)、若为的中点,且 , 求的面积;(3)、如图,过点在所在平面内作 , 且满足.求线段的最大值.
(1)、求角的大小;(2)、若为的中点,且 , 求的面积;(3)、如图,过点在所在平面内作 , 且满足.求线段的最大值. -
9、如图,在正三棱柱中, , 分别为棱 , 的中点,.
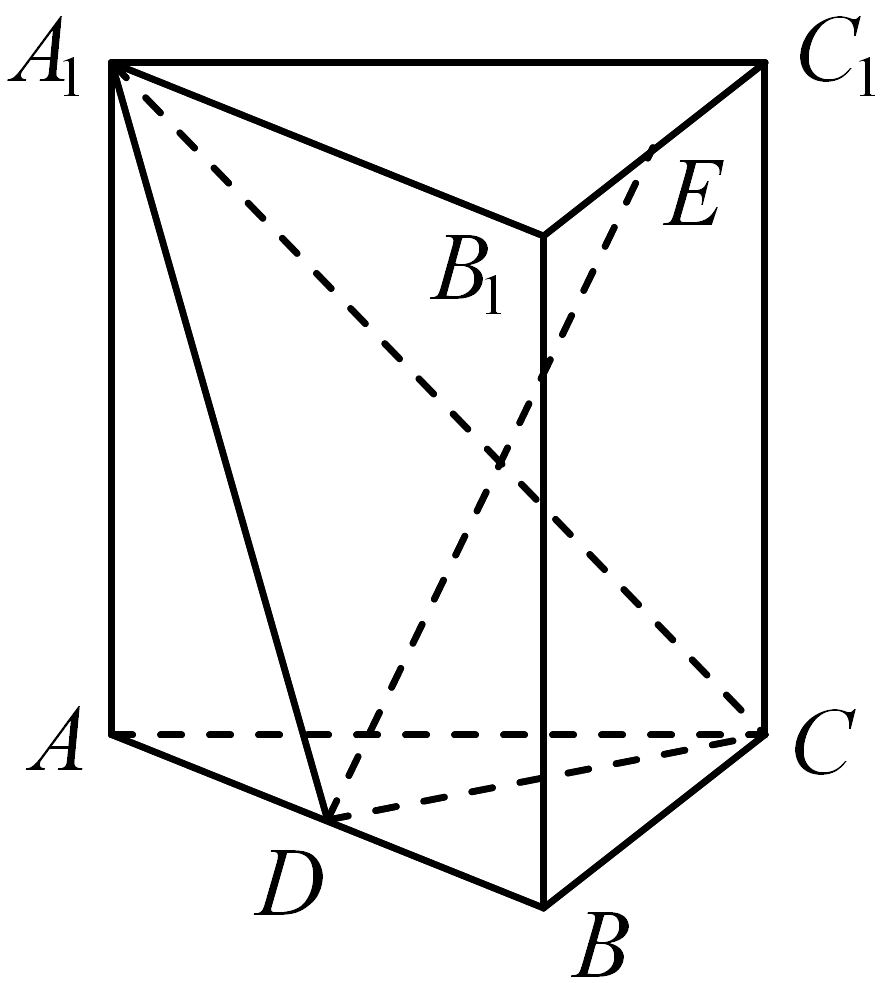 (1)、证明:平面;(2)、若三棱锥的体积为 , 求二面角的余弦值.
(1)、证明:平面;(2)、若三棱锥的体积为 , 求二面角的余弦值. -
10、“数学好玩”是国际著名数学家陈省身赠送给少年数学爱好者们的一句话.某校为了更好地培养学生创新精神和实践能力,激发学生钻研数学的兴趣和热情,特举办数学节活动.在活动中,共有20道数学问题,满分100分在所有的答卷中随机抽取100份作为样本,将样本的成绩分成六段: , , ……, , 得到如图所示的频率分布直方图.
 (1)、求频率分布直方图中a的值,并估计该校全体学生这次数学成绩的中位数;(2)、活动中,甲、乙、丙三位同学独立参加竞赛,已知甲同学答对了12道,乙同学答对了8道,丙同学答对了n道,假设每道数学问题难度相当,被答对的可能性都相同.
(1)、求频率分布直方图中a的值,并估计该校全体学生这次数学成绩的中位数;(2)、活动中,甲、乙、丙三位同学独立参加竞赛,已知甲同学答对了12道,乙同学答对了8道,丙同学答对了n道,假设每道数学问题难度相当,被答对的可能性都相同.(i)任选一道数学问题,求甲、乙两位同学恰有一人答对的概率;
(ii)任选一道数学问题,若甲、乙、丙三个人中至少有一个人答对的概率为 , 求n的值.
-
11、已知向量 , , 设.(1)、求的最小正周期;(2)、若 , , 求的值.
-
12、在圆台中,圆的半径是2,母线 , 圆是的外接圆, , , 则三棱锥体积最大值为 .
-
13、若(为虚数单位)为方程()的一个根,则.
-
14、已知向量 , , 则在上的投影向量的坐标是 .
-
15、一只不透明的口袋内装有9张卡片,上面分别标有数字1,2,3,…,9.从袋中任意抽取1张卡片,记“抽出的卡片号为1,4,7”为事件A,“抽出的卡片号小于7”为事件 , “抽出的卡片号大于7”记为事件.下列说法正确的是( )A、事件A与事件是互斥事件 B、事件A与事件是互斥事件 C、事件A与事件相互独立 D、事件与事件是对立事件
-
16、如图,在多面体中,四边形ABCD是边长为3的正方形, , E到平面ABCD的距离为3, , .若A,B,C,D,E,F在同一球面上,则该球的表面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、如图,在正方形中,点E、F分别是AB、BC的中点,将、分别沿DE、DF折起,使A,C两点重合于P,连接EF,PB.
 (1)、求证:;(2)、点M是PD上一点,若直线MF与平面所成角的正切值为 , 求二面角的余弦值.
(1)、求证:;(2)、点M是PD上一点,若直线MF与平面所成角的正切值为 , 求二面角的余弦值. -
18、在① , ② , ③这三个条件中任选一个作为已知条件,补充在下面的问题中,然后解答补充完整的题.
的内角A,B,C所对的边分别为a,b,c,已知___________(只需填序号).
(1)、求角;(2)、设是BC上一点,且 , , 求面积的最大值.注:若选择多个条件分别解答,则按第一个解答计分.
-
19、如图,平面 , , 平面.
 (1)、求证:;(2)、若 , , , 求三棱锥的体积.
(1)、求证:;(2)、若 , , , 求三棱锥的体积. -
20、文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创建者,某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取100份作为样本,将样本的成绩(满分100分,成绩均不低于40分)分成六段: , , …, , 得到如图所示的频率分布直方图.
 (1)、求频率分布直方图中a的值,并求样本成绩的第75百分位数;(2)、现从以上各段中采用样本量比例分配的分层随机抽样再抽取20份答卷作为“典型答卷”进一步统计研究,若落在的“典型答卷”的平均成绩与方差分别是82和8,落在的“典型答卷”的平均成绩与方差分别是96和1,据此估计这100份答卷中落在的所有答卷的成绩的方差.
(1)、求频率分布直方图中a的值,并求样本成绩的第75百分位数;(2)、现从以上各段中采用样本量比例分配的分层随机抽样再抽取20份答卷作为“典型答卷”进一步统计研究,若落在的“典型答卷”的平均成绩与方差分别是82和8,落在的“典型答卷”的平均成绩与方差分别是96和1,据此估计这100份答卷中落在的所有答卷的成绩的方差.