相关试卷
-
1、已知椭圆的左焦点为 , 左顶点为 , 直线过点 , 且与轴垂直,交于 , 两点,已知的周长为 , 则椭圆的离心率为( )A、 B、 C、 D、
-
2、已知直线 , 圆 , 为上一动点,则到的最小距离为( )A、1 B、2 C、3 D、4
-
3、某学校高二年级开设了乒乓球、羽毛球和篮球三门课,甲、乙两位同学每人从中选择一门,且允许多位同学选择同一门课.若至少有一位同学选择了乒乓球,则这两位同学不同的选课方法共有( )种.A、2 B、4 C、5 D、9
-
4、已知圆 , 圆 , 两圆的交点为 , , 则( )A、 B、1 C、 D、2
-
5、等差数列的前项和为 , , 则( )A、10 B、20 C、30 D、40
-
6、直线与直线一定( )A、平行 B、垂直 C、重合 D、相交但不垂直
-
7、向量( )A、 B、 C、 D、
-
8、“是“”的( )A、充分且不必要条件 B、必要且不充分条件 C、充要条件 D、既不充分也不必要条件
-
9、数据 , , , , 的平均数与众数的差为( )A、 B、 C、 D、
-
10、深圳是一个沿海城市,拥有大梅沙等多样的海滨景点,每年夏天都有大量游客来游玩.为了合理配置旅游资源,文旅部门对来大梅沙游玩的游客进行了问卷调查,据统计,其中的人选择只游览海滨栈道,另外的人选择既游览海滨栈道又到海滨公园游玩.每位游客若选择只游览海滨栈道,则记1分;若选择既游览海滨栈道又到海滨公园游玩,则记2分.假设游客之间的旅游选择意愿相互独立,视频率为概率.(1)、从游客中随机抽取2人,记这2人的合计得分为 , 求的分布列和数学期望;(2)、从游客中随机抽取个人 , 记这个人的合计得分恰为分的概率为 , 求;(3)、从游客中随机抽取若干人,记这些人的合计得分恰为分的概率为 , 随着抽取人数的无限增加,是否趋近于某个常数?若是,求出这个常数;若不是,请说明理由.
-
11、已知椭圆的右焦点为 , 点在上,且轴.(1)、求的方程;(2)、过点的直线交于两点,求面积的最大值.
-
12、如图,四棱锥中,平面平面 , 为棱上一点.
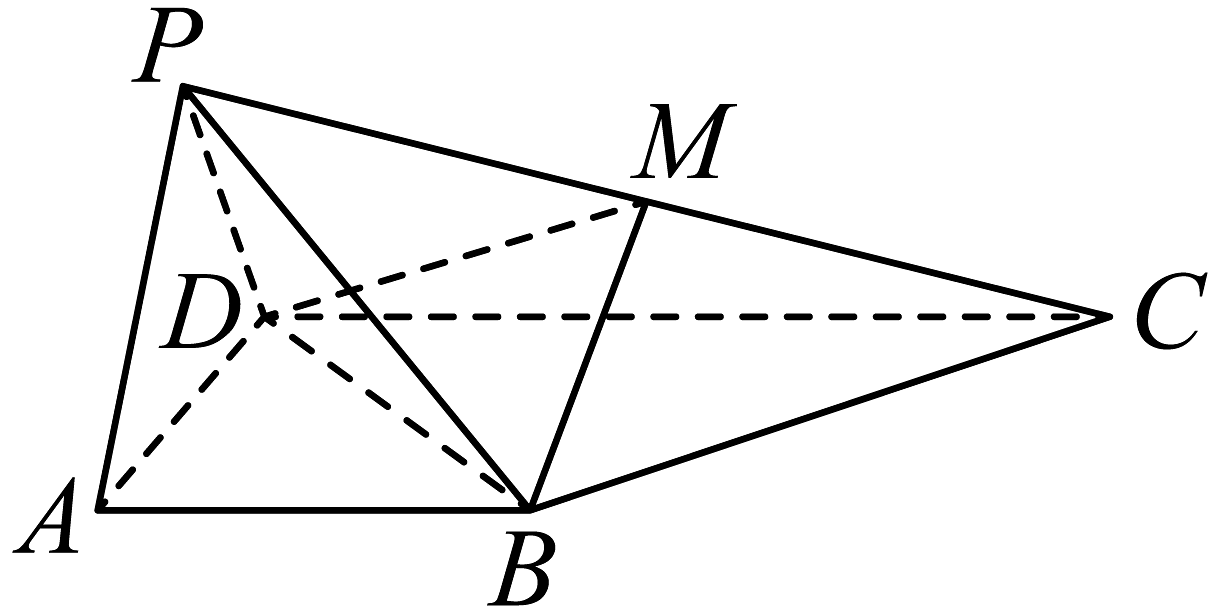 (1)、证明:;(2)、若平面 , 求直线与平面所成角的正弦值.
(1)、证明:;(2)、若平面 , 求直线与平面所成角的正弦值. -
13、已知的最小值为.
-
14、如图,等边的边长为4,为边的中点,将沿折成三棱锥 , , B,C,D都在球的球面上.记 , , 与平面所成的角分别为 , , , 平面 , , 与平面所成的角分别为 , , , 则( )
 A、与所成的角为定值 B、球的表面积的最大值为 C、 D、存在点使得
A、与所成的角为定值 B、球的表面积的最大值为 C、 D、存在点使得 -
15、已知函数的导函数为 , 下列判断正确的是( )A、函数关于中心对称,函数关于轴对称 B、在复数范围内方程有三个根,且三个根的和为3 C、时, D、四次函数必为轴对称函数
-
16、已知函数 , 对任意 , 都有 , 且存在 , 使得 , 则实数的取值范围是( )A、 B、 C、 D、
-
17、只用1,2,3这三个数字组成一个五位数,规定这三个数字必须全部使用,且同一数字不能相邻出现,这样的五位数共有( )A、30个 B、36个 C、42个 D、48个
-
18、已知的半径为 , 直线恒过点 , 且成等差数列,过点作的切线,则点到切点的距离为( )A、 B、 C、 D、
-
19、曲线在点 处的切线与直线和 围成的三角形的面积为( )A、 B、 C、 D、1
-
20、已知向量 , 满足 , , 且 , 则( )A、 B、 C、 D、