相关试卷
-
1、已知函数是定义域为的奇函数,当时,.
 (1)、求出函数的解析式;(2)、画出函数的图象,并写出函数的单调区间;(3)、根据图象写出使的x的取值集合.
(1)、求出函数的解析式;(2)、画出函数的图象,并写出函数的单调区间;(3)、根据图象写出使的x的取值集合. -
2、已知集合.(1)、求(2)、;(3)、若 , 求实数a的取值范围.
-
3、若函数的定义域为 , 值域为 , 则a的值可能为( )A、1 B、2 C、4 D、5
-
4、若正实数a,b满足 , 则下列说法正确的是( )A、有最小值9 B、有最大值 C、有最大值 D、有最小值
-
5、设 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
6、已知椭圆经过点 , 两个焦点为和.(1)、求椭圆的标准方程;(2)、直线过点且与椭圆相交于、两点, , 点与关于轴对称,点与关于轴对称,设直线的斜率为 , 直线的斜率为.
(i)求证:为定值,并求出这个定值;
(ii)若 , 求直线的方程.
-
7、设函数 , 曲线在点处的切线方程为.(1)、求的值;(2)、若在定义域内恰有2个零点,求的取值范围;(3)、记点 , 当时,曲线在点处的切线与轴交于点 , 求三角形面积的最大值.
-
8、在四棱锥中,底面是边长为2的正方形, , 直线与所成的角的余弦值等于 , , 点为线段上的动点,是的中点.
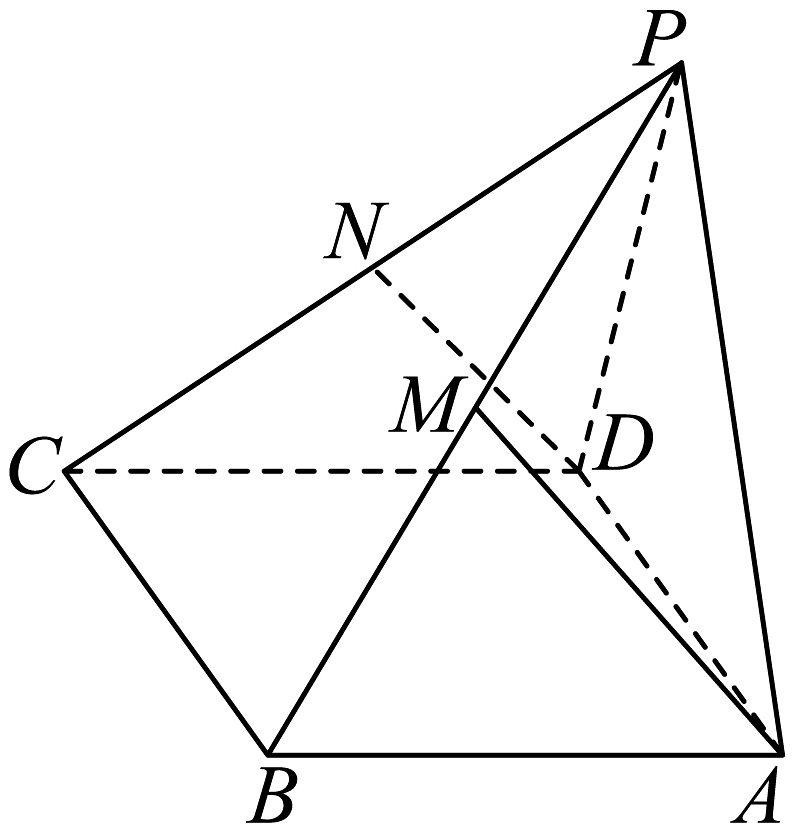 (1)、若直线和相交,求证:;(2)、求证:平面平面;(3)、当三棱锥的体积最大值时,求此时三棱锥外接球的体积.
(1)、若直线和相交,求证:;(2)、求证:平面平面;(3)、当三棱锥的体积最大值时,求此时三棱锥外接球的体积. -
9、某学校号召学生参加“每天锻炼1小时”活动,为了解学生参加活动的情况,统计了全校所有学生在假期每周锻炼的时间,现随机抽取了60名同学在某一周参加锻炼的数据,整理如下列联表:
性别
不经常锻炼
经常锻炼
合计
男生
7
女生
16
30
合计
21
注:将一周参加锻炼时间不小于3小时的称为“经常锻炼”,其余的称为“不经常锻炼”.
(1)、请完成上面列联表,并依据小概率值的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;(计算结果精确到小数点后三位)(2)、将频率视为概率,从学校不经常锻炼的学生中抽取4人,设抽取的4人中男生人数为 , 求的分布列和数学期望.附: ,
0.1
0.05
0.01
2.706
3.841
6.635
-
10、已知定义在实数集上的函数满足 , 则的取值范围为 .
-
11、抛物线C:的焦点为F,准线为l,M是C上的一点,点N在l上,若 , 且 , 则.
-
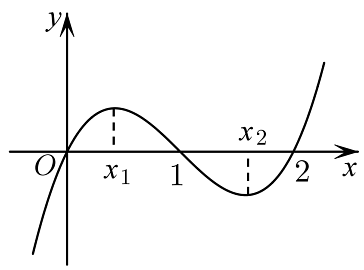
12、已知函数的图象如图所示,则.
-
13、已知函数 , 则下列说法中正确的是( )A、 B、的最大值是 C、在上单调递增 D、若函数在区间上恰有个极大值点,则的取值范围为
-
14、下列选项中,正确的命题是( )A、已知随机变量 , 若 , , 则 B、的展开式中的系数为10. C、用独立性检验进行检验时,的值越大,说明有更大的把握认为两事件有关系. D、样本相关系数越接近1,成对样本数据的线性相关程度越强.
-
15、已知的内角A,B,C的对边分别为a,b,c,且 , 则( )A、 B、 C、 D、
-
16、已知关于的函数图象如图所示,则实数满足的关系式可以为( )
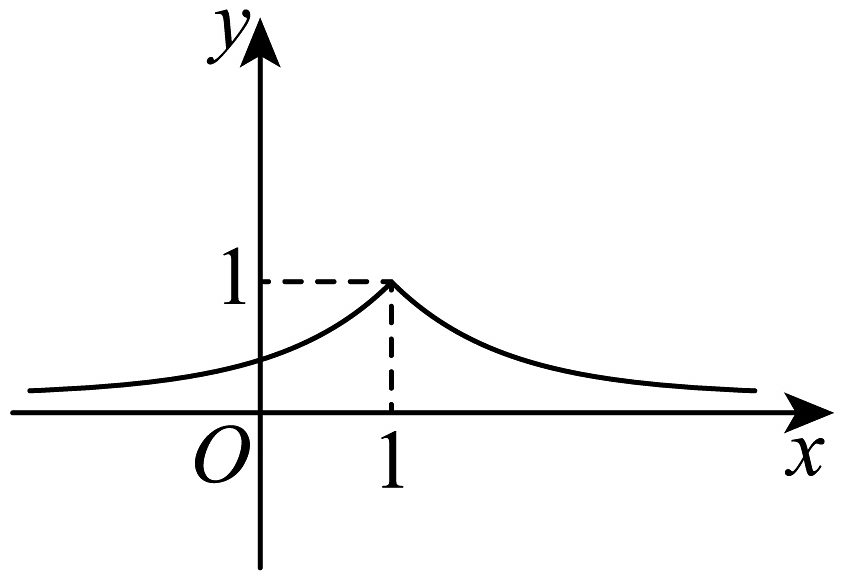 A、 B、 C、 D、
A、 B、 C、 D、 -
17、以模型去拟合一组数据时,为了求出回归方程,设 , 将其变换后得到经验回归方程 , 则的值分别是( )A、 B、 C、 D、
-
18、已知集合 , 则( )A、 B、 C、 D、
-
19、已知复数满足 , 则的虚部为( )A、-1 B、 C、1 D、i
-
20、已知函数 , 若函数恰有3个不同的零点,则实数的取值范围是( )A、 B、 C、 D、