相关试卷
- 江苏省扬州市高邮市2017-2018学年高一上学期数学期中考试试卷
- 江苏省扬州市高邮市2017-2018学年高二上学期数学期中考试试卷
- 2017-2018学年江苏省盐城市2017-2018学年高三上学期数学期中考试试卷
- 江苏省徐州市2017-2018学年高三上学期数学期中考试试卷
- 江苏省泰州市靖江市2017-2018学年高一上学期数学期中考试试卷
- 江苏省泰州市靖江市2017-2018学年高二上学期数学期中考试试卷
- 江苏省苏州市常熟市2017-2018学年高二上学期数学期中考试试卷
- 江苏省南通市2017-2018学年高二上学期数学期中考试试卷
- 江苏省淮安市、宿迁市2017-2018学年高三上学期数学期中考试试卷
- 江苏省常州市武进区2017-2018学年高三上学期理数期中考试试卷
-
1、命题“ , ”的否定为.
-
2、下列选项中正确的是( )A、已知集合 , 若 , 则 B、若不等式的解集为 , 则 C、若集合满足 , 则满足条件的集合有8个 D、已知集合 , 若 , 则的取值范围为
-
3、下列说法中正确的是( )A、若 , , 则: B、若 , , 则: C、若 , , 则: D、若 , , 则:
-
4、下列命题正确的有( )A、 , B、 , C、 , D、 ,
-
5、关于的不等式的解集中恰有1个整数,则实数的取值范围为( )A、或 B、或 C、或 D、或
-
6、某快递公司为降低新冠肺炎疫情带来的经济影响,引进智能机器人分拣系统,以提高分拣效率和降低物流成本.已知购买台机器人的总成本为(单位:万元).若要使每台机器人的平均成本最低,则应买机器人( )A、100台 B、200台 C、300台 D、400台
-
7、已知全集 , 集合 , 集合 , 用如图所示的阴影部分表示的集合为( )
 A、{2,4} B、{0,3,5,6} C、{0,2,3,4,5,6} D、{1,2,4}
A、{2,4} B、{0,3,5,6} C、{0,2,3,4,5,6} D、{1,2,4} -
8、不等式的解集是( )A、 B、或 C、或 D、或
-
9、以下命题既是存在量词命题又是真命题的是( )A、锐角三角形有一个内角是钝角 B、至少有一个实数 , 使 C、两个无理数的和必是无理数 D、存在一个负数 , 使
-
10、设集合 , , 则( )A、 B、 C、 D、
-
11、已知四棱锥如图,且 , , 分别是 , 的中点,则下列说法正确的有( )
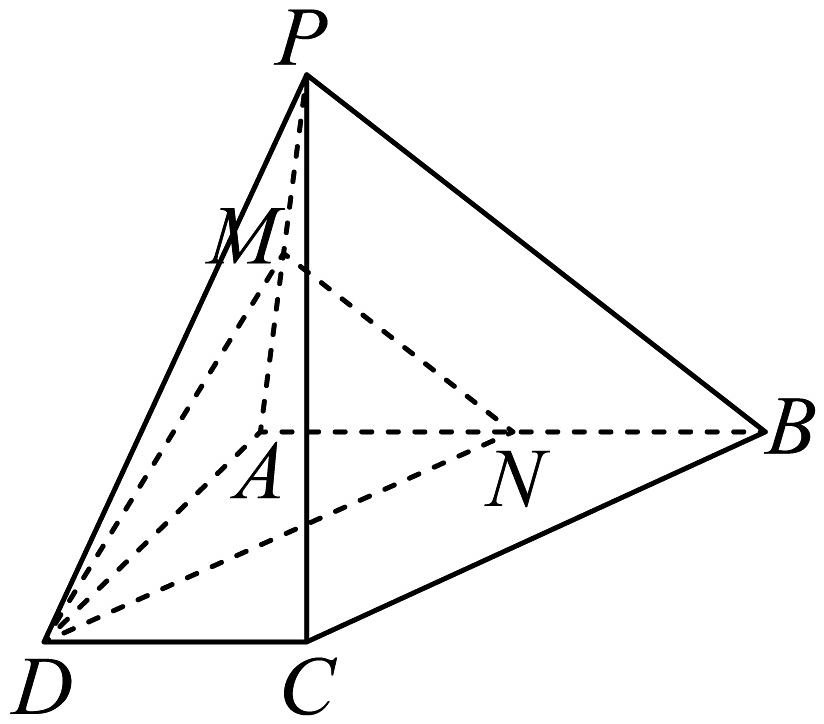 A、平面 B、四棱锥的体积为 , 三棱锥的体积为 , 则 C、平面与平面的交线记为 , 则直线平面 D、平面与平面的交线记为 , 则直线平面
A、平面 B、四棱锥的体积为 , 三棱锥的体积为 , 则 C、平面与平面的交线记为 , 则直线平面 D、平面与平面的交线记为 , 则直线平面 -
12、若是数据的第75百分位数,则二项式的展开式的常数项是( )A、240 B、90 C、12 D、5376
-
13、已知向量若则( )A、 B、 C、1 D、2
-
14、已知 , , 且 , 则( )A、4 B、2 C、 D、1
-
15、已知函数 , 其中 .(1)、讨论函数的单调性;(2)、已知 , 若对任意的恒成立,求的最小值.
-
16、在中,内角的对边分别为 , 且满足.(1)、求;(2)、若为边上一点(异于端点), , 求的取值范围.
-
17、已知抛物线的焦点为 , 斜率为的直线与交于两个不同的点 , 且为线段的一个三等分点,则( )A、4 B、8 C、12 D、16
-
18、对于给定的项整数数列:(),定义变换:①若 , 则加 , 均加 , 其余项不变;②若 , 则加 , 均加 , 其余项不变;③若 , 则加 , 均加 , 其余项不变.例如,对数列:做变换得到 , 即;而对数列:先后做变换 , 可得到 , 即 .(1)、找出一系列变换,使得数列:经过这系列变换后成为常数列;(2)、是否能找出一系列变换,使得数列:经过这系列变换后成为常数列,若存在,请给出具体的变换;若不存在,请说明理由;并请判断当为奇数时,对于任意数列 , 是否总存在一系列变换能使该数列成为常数列(无须证明).(3)、当为偶数且数列是递增数列时,是否存在一系列变换,使得该数列成为常数列,若存在,请给出具体的变换;若不存在,请说明理由.
-
19、已知函数(),为坐标原点.(1)、当时,
(i)求曲线在点处的切线方程;
(ii)若点是函数图象上一点,求的最小值;
(2)、若函数图象上存在不同两点满足 , 求的取值范围. -
20、已知双曲线()的左,右焦点分别为 , 且 , 圆与的渐近线相切.(1)、求双曲线的标准方程;(2)、若上两点满足(),且四边形的面积为 , 求的值.