-
1、已知函数的图象如图所示,点 , , 为与轴的交点,点 , 分别为的最高点和最低点,而函数的相邻两条对称轴之间的距离为 , 且其在处取得最小值.
 (1)、求参数和的值;(2)、若 , 求向量与向量的夹角;(3)、若点为函数图象上的动点,当点在 , 之间运动时,恒成立,求的取值范围.
(1)、求参数和的值;(2)、若 , 求向量与向量的夹角;(3)、若点为函数图象上的动点,当点在 , 之间运动时,恒成立,求的取值范围. -
2、如图,平行四边形的两条对角线相交于点C,点满足 , , 设 , , 且 .
 (1)、用 , 表示;(2)、若 , 求 .
(1)、用 , 表示;(2)、若 , 求 . -
3、已知向量 , , 函数 .(1)、求函数图象的对称轴;(2)、若在上有解,求整数m的最小值.
-
4、在① , ② , ③中任选一个条件,补充在下面问题中,并解决问题.
已知 , _____,.
(1)求的值;
(2)求.
-
5、已知向量满足 , 且 , .(1)、求;(2)、求与的夹角(3)、求.
-
6、已知 , 求(1)、及的值;(2)、
-
7、如图,在△ABC中, , , , M是BC边上的中点,P是AM上一点,且满足 , 则.

-
8、已知扇形的圆心角为 , 弧长为 , 则该扇形的面积为 .
-
9、将函数图象上所有点的横坐标缩短到原来的(纵坐标不变),再向左平移个单位长度,所得图象对应的函数为 , 若在上有且仅有5个零点,则( )A、 B、在单调递增 C、的取值范围是 D、在有且仅有3个零点
-
10、对于任意的两个向量 , , , 下列命题一定正确的是( )A、 B、 C、 D、
-
11、已知是边长为1的正的边上的动点,为的中点,则的取值范围是( )A、 B、 C、 D、
-
12、已知 , , 且 , 则与的夹角为( )A、0° B、90° C、135° D、180°
-
13、如图,在矩形中,为中点,那么向量等于( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、若角的终边与单位圆的交点坐标是 , 则( )A、 B、 C、 D、
-
15、下列向量组中,能作为表示它们所在平面内的所有向量的基底的是( )A、 , B、 , C、 , D、 ,
-
16、如图,斜三棱柱中,底面是正三角形,分别是侧棱上的点,且 , 设直线与平面所成的角分别为 , 平面与底面所成的锐二面角为 , 则( )
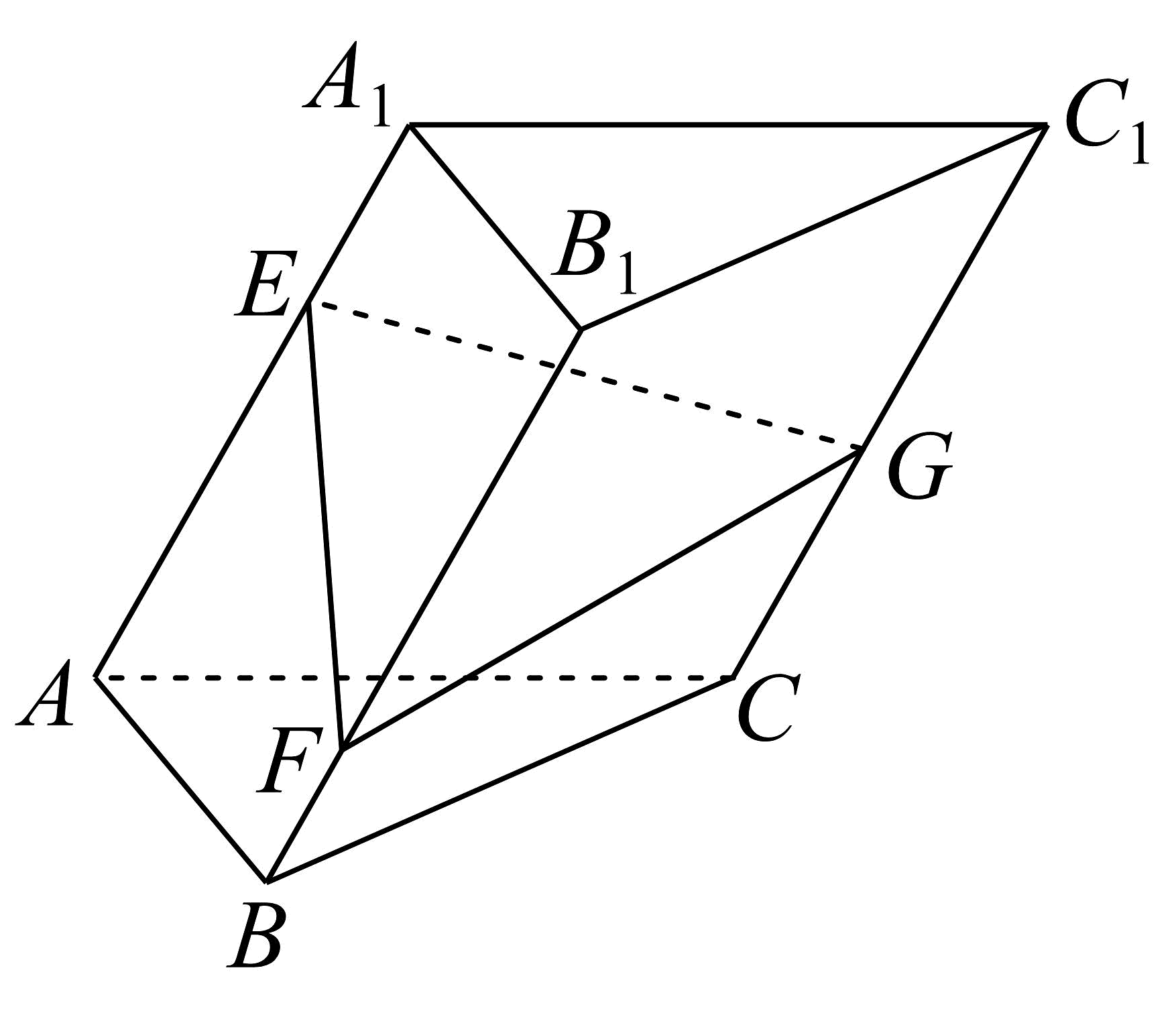 A、 B、 C、 D、
A、 B、 C、 D、 -
17、在中,角、、所对的边分别为、、 , 且 , .(1)、求;(2)、若为锐角三角形,求的面积范围.
-
18、已知正的边长为1,中心为 , 过的动直线与边分别相交于点 .
 (1)、若 , 求 .(2)、求与的面积之比的最小值.
(1)、若 , 求 .(2)、求与的面积之比的最小值. -
19、已知角是的内角,若 , .
(1)若 , 求角A的值;
(2)设 , 当取最大值时,求在上的投影向量(用坐标表示).
-
20、已知复数( , 为虚数单位).(1)、当时,求;(2)、设为复数z的共轭复数,若不是纯虚数,求m的取值范围.