-
1、如图1,在直角梯形中, , , , , 为的中点.将沿翻折,使点到点的位置,且 , 得到如图2所示的四棱锥 , 若为的中点,是棱上动点.
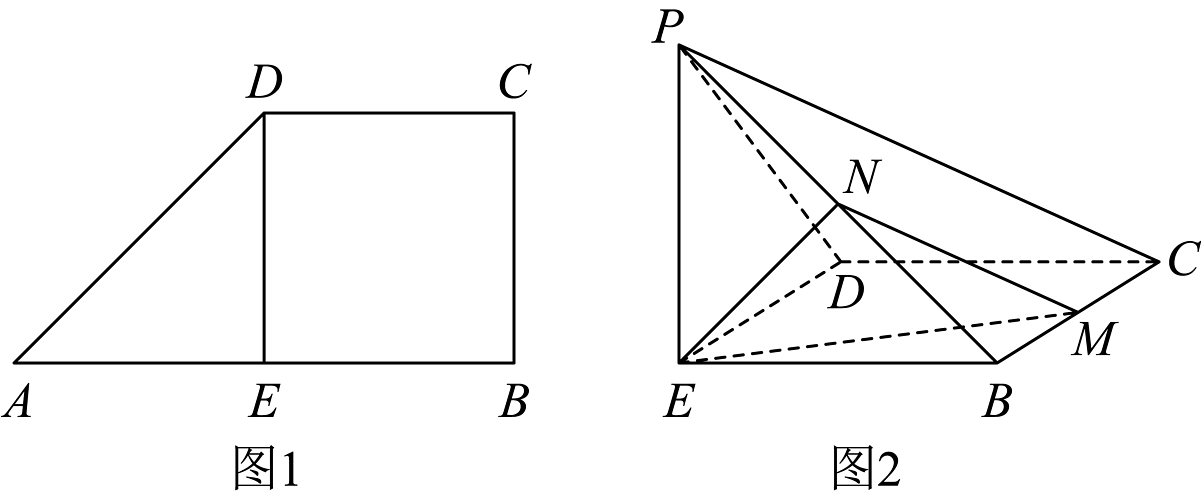 (1)、当为的中点时.
(1)、当为的中点时.①求证:平面平面;
②求直线与平面所成角的正弦值.
(2)、若 , 求二面角的正弦值的取值范围. -
2、已知、、分别为三个内角、、的对边,且.(1)、求的值;(2)、若 , , 的面积为 , 求的值;(3)、若 , , 为垂心,为的外心,求的值.
-
3、如图,中, , , , , N为的中点,设 , 与相交于点.
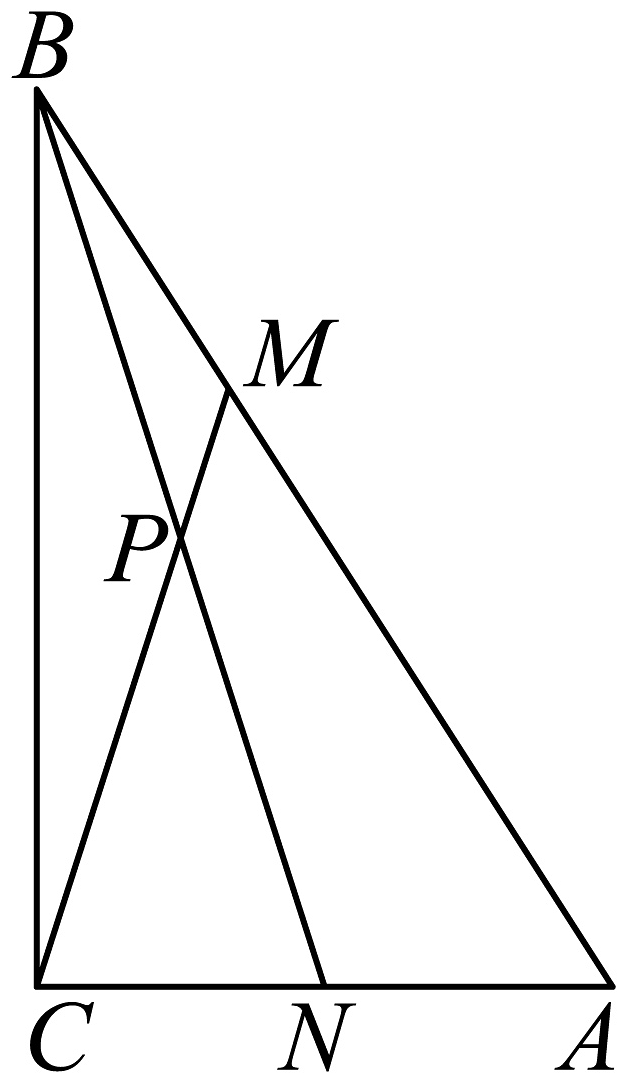 (1)、用 , 表示、;(2)、若 , 求的值;(3)、求.
(1)、用 , 表示、;(2)、若 , 求的值;(3)、求. -
4、在三棱锥中,平面平面 , , 为的中点.
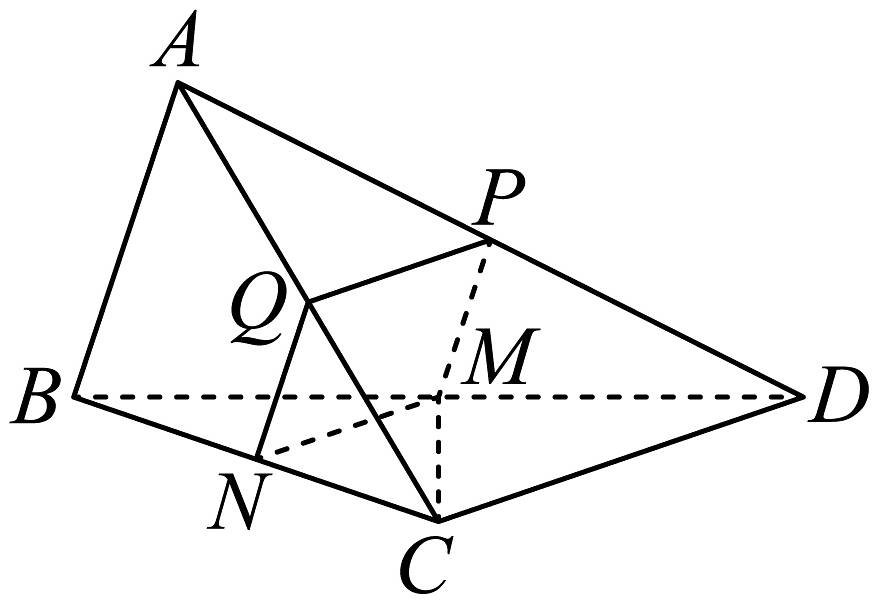 (1)、求证:;(2)、若为的中点,过的平面交平面于 , 求证:平面.
(1)、求证:;(2)、若为的中点,过的平面交平面于 , 求证:平面. -
5、已知函数.(1)、求函数的值域;(2)、求使成立的的取值集合.
-
6、在三角恒等变化中,积化和差实际上就是把与 , 与相加或相减而变形得到的;和差化积实际上就是一种角的变化,如:.
如果角与满足 , , 则.
-
7、已知a,b,c分别为三个内角A,B,C的对边,若 , , , 则.
-
8、的值为.
-
9、已知函数 , , 则下列说法正确的是( )A、时,点是函数图象的一个对称中心 B、时,函数在上有4个零点 C、将图象向左平移个单位长度后,得到的函数图象关于轴对称,则最小值为3 D、当时,恰有4个最大值,则实数的取值范围为
-
10、如图,在正三棱柱中, , , 则下列说法正确的是( )
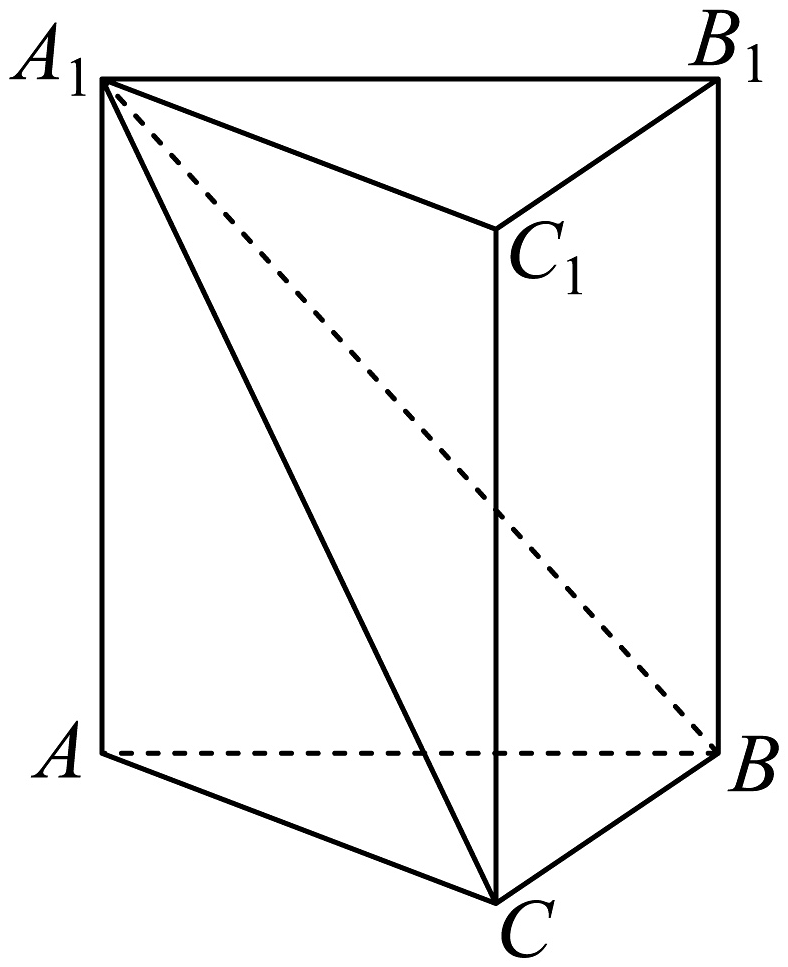 A、直线与直线所成角为 B、三棱锥的体积为 C、点到平面的距离为 D、四棱锥的外接球的表面积为
A、直线与直线所成角为 B、三棱锥的体积为 C、点到平面的距离为 D、四棱锥的外接球的表面积为 -
11、在中,下列说法正确的是( )A、 B、 C、若 , 则 D、存在 , 使得成立
-
12、如图,正方体中,为的中点,点为四边形及其内部的动点,平面.则与平面所成角正切值的范围( )
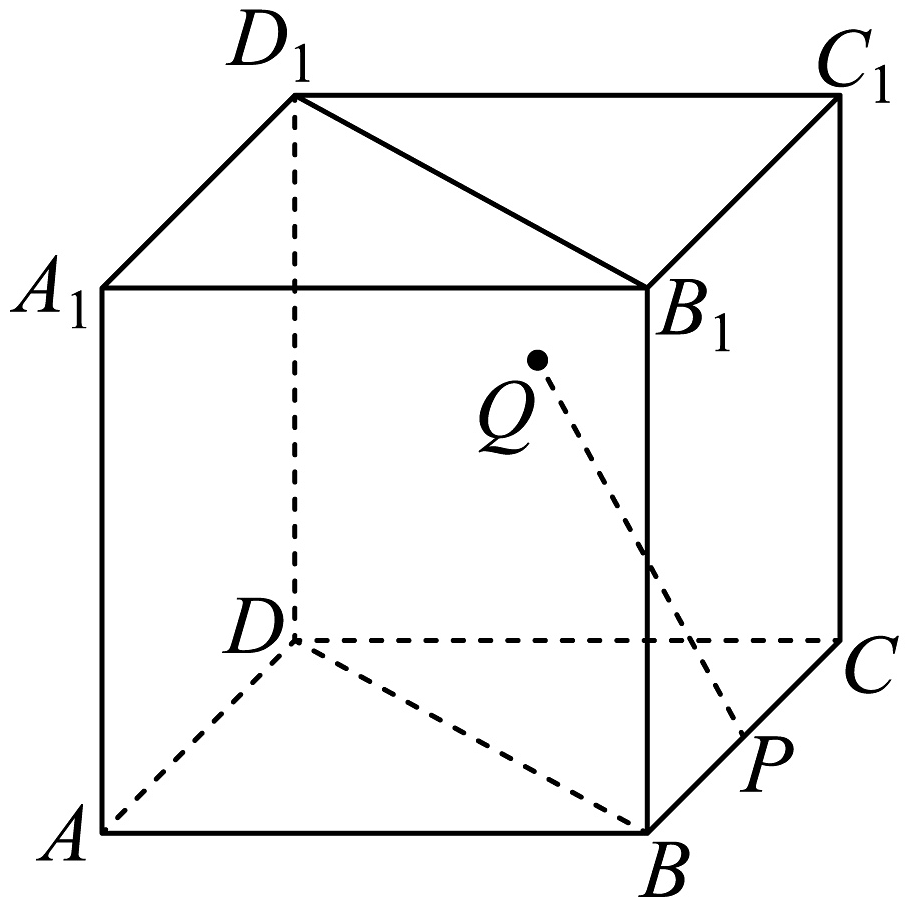 A、 B、 C、 D、
A、 B、 C、 D、 -
13、如图,在中, , 于 , , , 则在上的投影向量为( )
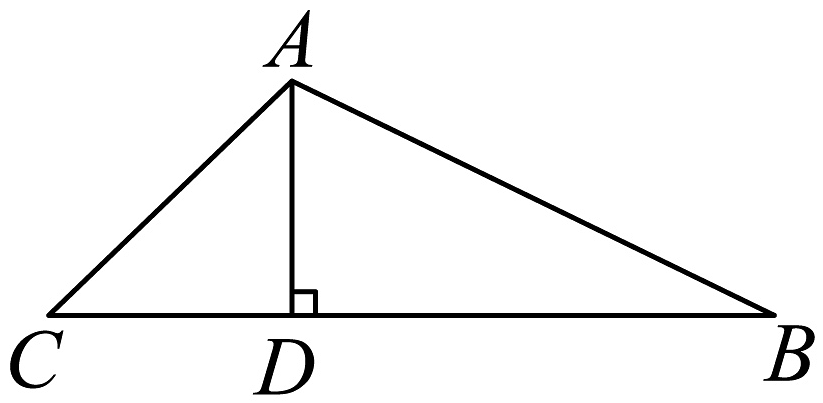 A、 B、 C、 D、
A、 B、 C、 D、 -
14、已知中, , , 则的面积为( )A、 B、 C、 D、
-
15、如图,已知圆锥的轴截面是边长为4的正三角形,则该圆锥的侧面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、设 , 为不同的平面,m,n为不同的直线,则下列说法中正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , , 则
-
17、已知 , , 则( )A、 B、 C、 D、
-
18、已知平面向量 , , 若 , 则( )A、 B、 C、2 D、3
-
19、设为虚数单位,复数 , 则在复平面内对应的点在第( )象限.A、一 B、二 C、三 D、四
-
20、已知向量 , 在上的投影向量为 , 则( )A、 B、8 C、4 D、