-
1、某同学在用打点计时器研究匀变速直线运动规律的实验中打出的点如图所示,在纸带上确定出A、B、C、D、E、F、G共7个计数点,其相邻点间的距离如图所示。

(1)打点计时器使用电源(选填“交流”或“直流”),电源的频率是50Hz,每相邻两个计数点之间有四个点未画出,则每两个相邻的计数点之间的时间间隔为秒。
(2)计算出打下C、D两点时小车的瞬时速度(保留三位有效数字):vC=m/s,vD=m/s
(3)计算加速度:a=m/s2(保留二位有效数字)。
-
2、有一种蜘蛛带电后能在电场环境中“御电飞行”。如图所示,在一个固定的带正电的金属球旁边,一只带负电的蜘蛛在水平面上做半径为R的匀速圆周运动。若金属球半径为R,所带电荷量为+Q,蜘蛛可看做质点且质量为m,其到球面的距离和到过O点竖直线的距离均为R(已知均匀带电球壳内部电场强度为0,且金属球电荷分布均匀),蜘蛛所带电量不影响金属球电荷分布,重力加速度为g,静电力常量为k,忽略空气阻力,则下列说法正确的是( )
 A、蜘蛛受到的电场力为 B、蜘蛛的动能为 C、金属球内一点P,已知OP=0.5R,则P点的电场强度大小为 D、蜘蛛所带电量为
A、蜘蛛受到的电场力为 B、蜘蛛的动能为 C、金属球内一点P,已知OP=0.5R,则P点的电场强度大小为 D、蜘蛛所带电量为 -
3、一个质点在平衡位置O点附近做简谐运动,若从O点开始计时,经过2s质点第一次经过M点,再继续运动,又经过1 s它第二次经过M点;则该质点第三次经过M点再需要的时间可能是( )A、 B、 C、7 s D、9 s
-
4、长沙市某游乐场有高山坡滑草这项游乐项目:高山两侧是坡度不同的滑道,游客坐在滑草板上从顶端滑到水平地面,体验极速的刺激。如图所示,若两名质量相同的游客同时从顶端分别沿两侧滑面从静止开始下滑,若不考虑滑道的摩擦,则( )
 A、两人到达斜面底端时的速度相同 B、两人下滑过程中重力的冲量相同 C、两人下滑过程中合外力的冲量相同 D、两人下滑过程中动量变化量的大小相同
A、两人到达斜面底端时的速度相同 B、两人下滑过程中重力的冲量相同 C、两人下滑过程中合外力的冲量相同 D、两人下滑过程中动量变化量的大小相同 -
5、原子弹是利用重核裂变的链式反应制成的,在极短的时间内能够释放大量的核能,发生猛烈爆炸。1964年10月16日中国自行制造的第一颗原子弹爆炸成功,有力地打破了西方国家的核垄断和核讹诈,提高了中国的国际地位。下列核反应方程式中属于原子弹爆炸的核反应方程式的是( )A、 B、 C、 D、
-
6、新年将至,同学们都开始进行大扫除,如图所示,某同学通过拖把杆给墩布施加一方向与地面成斜向下、大小的作用力,使墩布沿水平地面匀速运动。假设拖把头的质量为1kg,拖把杆的质量不计,取重力加速度大小 , , , , 。
(1)求拖把头与地板间的动摩擦因数μ。
(2)若打扫一倾角为37°的斜坡时,该同学通过拖把杆给墩布施加一水平方向的作用力 , 使墩布沿斜坡向上匀速运动,假设此时动摩擦因数与拖把头与地板间的动摩擦因数μ相同,求的大小。
(3)当拖把静止在水平面时时,对拖把头施加一个沿拖把杆向下的力 , 拖把杆与地面的夹角为θ。当θ增大到某一值时,无论多大,都不能推动拖把头,求此时的值。(为方便起见,忽略拖把头的重力,且最大静摩擦力等于滑动摩擦力)

-
7、如图所示,质量为m的手机放在支架的斜面上,斜面与水平面的夹角为θ,手机处于静止状态。已知重力加速度为g。
 (1)、画出手机的受力示意图;(2)、求手机受到的摩擦力大小;(3)、调节斜面倾角到α时,手机恰好能沿斜面匀速下滑,求手机与斜面间的动摩擦因数μ。
(1)、画出手机的受力示意图;(2)、求手机受到的摩擦力大小;(3)、调节斜面倾角到α时,手机恰好能沿斜面匀速下滑,求手机与斜面间的动摩擦因数μ。 -
8、据悉,中国正在研发“不停站高铁”,方案之一是在高铁顶部设立吊舱,称为吊舱方案。如图所示,高铁列车在平直的铁轨上以288km/h的速度匀速行驶,在离站台3km处开始做匀减速运动,到达站台时刚好减到72km/h,进站吊舱B与高铁车分离,并在减速区停下,高铁车则与已在吊舱加速区加速到72km/h的出站吊舱A对接,并以进站时相同大小的加速度匀加速到288km/h。车厢、吊舱、站台均可看成质点,求
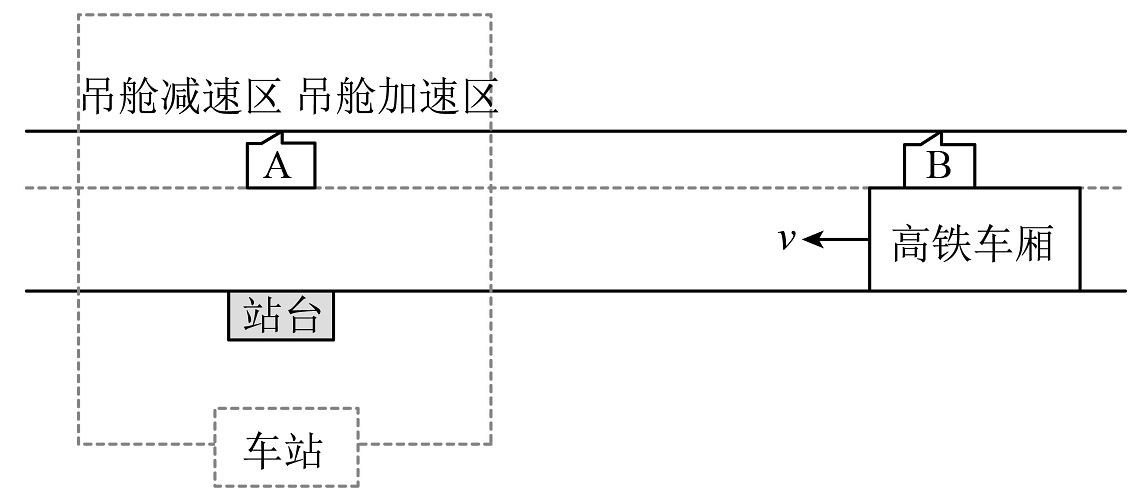 (1)、高铁列车进站的加速度大小;(2)、目前,高铁列车仍采用停车方案进站。其以288km/h做匀减速运动,经100s后停下,停留5min供乘客上下车,之后以相同大小的加速度匀加速至288km/h。
(1)、高铁列车进站的加速度大小;(2)、目前,高铁列车仍采用停车方案进站。其以288km/h做匀减速运动,经100s后停下,停留5min供乘客上下车,之后以相同大小的加速度匀加速至288km/h。①列车从开始减速到恢复正常行驶所通过的位移大小;
②对比停车方案,吊舱方案节省的时间。
-
9、某同学用如图所示的实验装置来“验证力的平行四边形定则”。弹簧测力计A挂于固定点P,下端用细线挂一重物M。弹簧测力计B的一端用细线系于O点,手持另一端向左拉,使结点O静止在某位置。分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线的方向。(1)、该实验运用的思想方法是______。A、等效替代法 B、控制变量法 C、理想模型法(2)、本实验用的弹簧测力计示数的单位为N,图中的示数为。
 (3)、下列的实验要求必要或者正确的是______(填选项前的字母)。A、应用测力计测量重物M所受的重力 B、应在水平桌面上进行实验 C、拉线方向应与木板平面平行 D、改变拉力,进行多次实验,每次都要使O点静止在同一位置(4)、在作图时,你认为图中是正确的。(填“甲”或“乙”)
(3)、下列的实验要求必要或者正确的是______(填选项前的字母)。A、应用测力计测量重物M所受的重力 B、应在水平桌面上进行实验 C、拉线方向应与木板平面平行 D、改变拉力,进行多次实验,每次都要使O点静止在同一位置(4)、在作图时,你认为图中是正确的。(填“甲”或“乙”)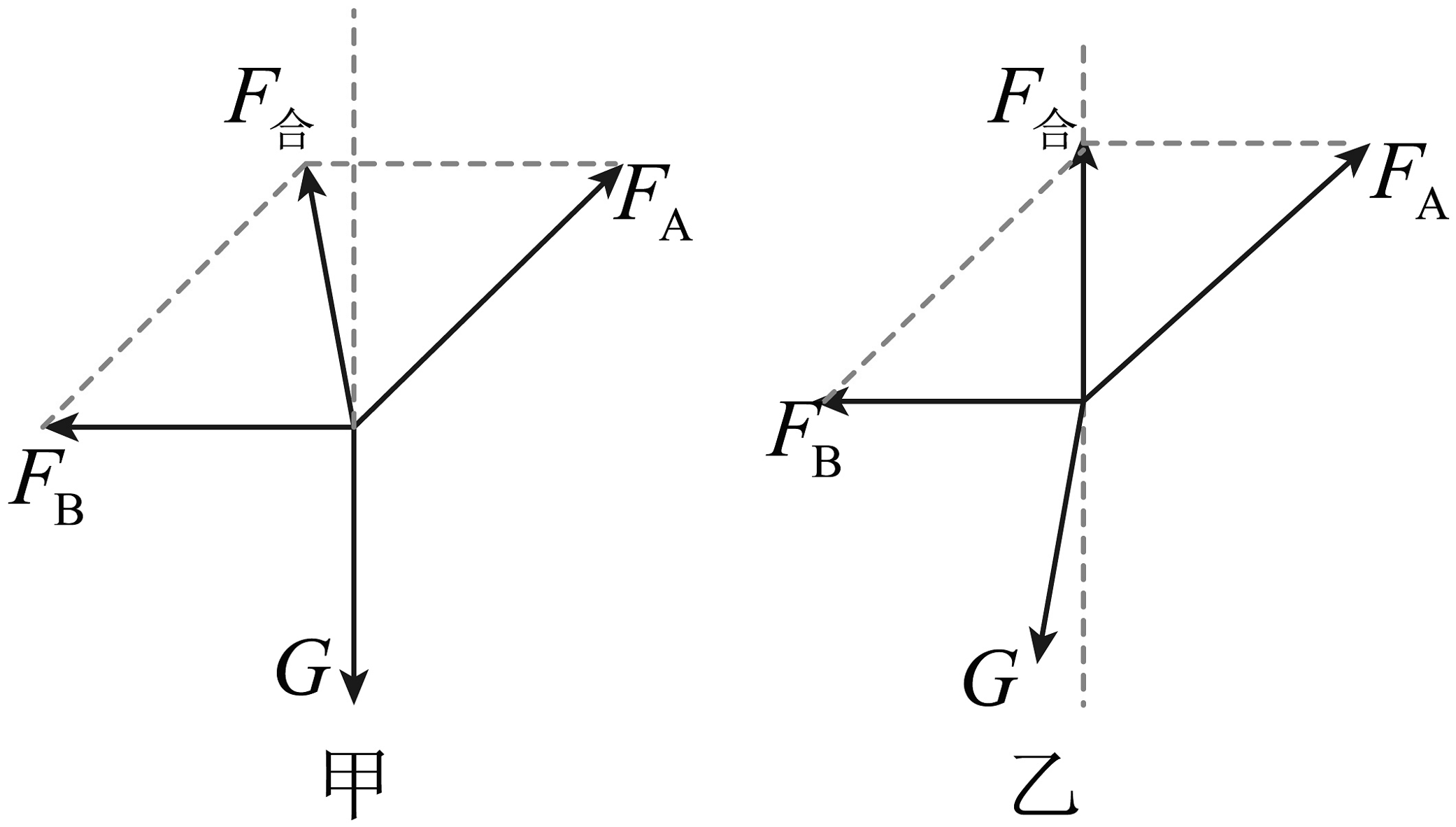
-
10、图中的甲、乙是高中物理实验中常用的两种打点计时器,请回答下面的问题:
(1)图乙是(填“电磁打点计时器”或“电火花计时器”),电源采用的是;(填“交流”“交流”或“四节蓄电池”);

(2)某同学在“探究小车速度随时间变化的规律”的实验中,关于轨道末端滑轮高度的调节正确的是;
A.
 B.
B. C.
C.
(3)该同学用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点,相邻两点间的距离如图丙所示,每两个相邻的计数点之间还有4个点未画出。
①试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并填入下表中;(结果保留三位有效数字)

速度
数值
0.400
0.479
0.560
0.640
②将B、C、D、E、F对应的瞬时速度标在图丁所示的直角坐标系中,并画出小车的瞬时速度随时间变化的关系图线;

③由速度—时间图像可得小车的加速度为。(结果保留两位小数)
-
11、如图所示,甲、乙两人分别乘坐两种电动扶梯,此时两电梯均匀速向上运转,则( )
 A、甲受到三个力的作用 B、甲对扶梯没有摩擦力的作用 C、乙受到两个力的作用 D、扶梯对乙的作用力方向竖直向上
A、甲受到三个力的作用 B、甲对扶梯没有摩擦力的作用 C、乙受到两个力的作用 D、扶梯对乙的作用力方向竖直向上 -
12、如图所示,为港珠澳大桥上连续四段110m的等距跨钢箱梁桥,若汽车从a点由静止开始做匀加速直线运动,通过ab段的时间为t,则( )
 A、通过ac段的时间为 B、通过cd段的时间为 C、ac段的平均速度小于b点的瞬时速度 D、ac段的平均速度等于b点的瞬时速度
A、通过ac段的时间为 B、通过cd段的时间为 C、ac段的平均速度小于b点的瞬时速度 D、ac段的平均速度等于b点的瞬时速度 -
13、下面图像描述的是A、B两物体做直线运动的相关图像。关于甲、乙、丙、丁四个图像,下列说法正确的是( )
 A、甲图中在t1~t2时间内,A的平均速度大于B的平均速度 B、乙图中的物体一定做往复运动 C、丙图中两物体在t1、t2两个时刻相遇两次 D、由丁图可以求出运动物体的加速度
A、甲图中在t1~t2时间内,A的平均速度大于B的平均速度 B、乙图中的物体一定做往复运动 C、丙图中两物体在t1、t2两个时刻相遇两次 D、由丁图可以求出运动物体的加速度 -
14、如图所示,小车内沿竖直方向的一根轻质弹簧和一条与竖直方向成角的细绳拴接一小球。当小车与小球相对静止,一起在水平面上匀速运动时,下列说法正确的是( )
 A、小球受到三个力的作用 B、轻弹簧一定被压缩 C、细绳一定对小球有拉力 D、细绳不一定对小球有拉力,轻弹簧对小球也不一定有弹力
A、小球受到三个力的作用 B、轻弹簧一定被压缩 C、细绳一定对小球有拉力 D、细绳不一定对小球有拉力,轻弹簧对小球也不一定有弹力 -
15、把一个苹果竖直向上抛出,苹果在空中受到重力和空气阻力的作用。若苹果在上升和下降过程中所受合力的大小分别为F1、F2 , 则( )A、Fl可能小于F2 B、Fl可能等于F2 C、Fl一定等于F2 D、Fl一定大于F2
-
16、陕西省青少年陆地冰壶比赛中,运动员将冰壶投出后,冰壶在轨道上做匀减速直线运动,用时10s停止,最后1s内的位移大小为0.2m,则下列说法正确的是( )
 A、冰壶的初速度大小为6m/s B、冰壶第1s内的位移大小为4m C、冰壶全程的平均速度大小为2m/s D、冰壶的加速度大小为0.2m/s2
A、冰壶的初速度大小为6m/s B、冰壶第1s内的位移大小为4m C、冰壶全程的平均速度大小为2m/s D、冰壶的加速度大小为0.2m/s2 -
17、雨后,屋檐还在不断滴着水滴。如图所示,小红同学认真观察后发现,这些水滴都是在质量积累到足够大时才由静止开始下落,每隔相等时间滴下一水滴,水滴在空中的运动情况都相同,某时刻起,第一颗水滴刚运动到窗台下边沿时,第4颗水滴恰欲滴下。她测得,屋檐到窗台下边沿的距离为 , 窗户的高度为。不计空气阻力的影响。则下列结论错误的是(重力加速度g取10m/s2)( )
 A、水滴下落到达窗台下边沿时的速度大小 B、每隔滴下一水滴 C、水滴经过窗户的时间 D、水滴经过窗户的平均速度为
A、水滴下落到达窗台下边沿时的速度大小 B、每隔滴下一水滴 C、水滴经过窗户的时间 D、水滴经过窗户的平均速度为 -
18、如图所示,用压力F将物体A、B紧压在竖直的墙壁上保持静止状态。下列说法错误的是( )
 A、物体A受力平衡 B、压力F与墙壁对物体B的支持力不是一对平衡力 C、物体A对物体B的压力与物体B对物体A的支持力是一对相互作用力 D、物体B所受的重力与墙壁对物体B的摩擦力是一对平衡力
A、物体A受力平衡 B、压力F与墙壁对物体B的支持力不是一对平衡力 C、物体A对物体B的压力与物体B对物体A的支持力是一对相互作用力 D、物体B所受的重力与墙壁对物体B的摩擦力是一对平衡力 -
19、如图所示,a、b两个物体叠放在一起,a靠在竖直墙壁上,在方向竖直向上的力F作用下,a、b静止不动,则下列说法正确的是( )
 A、b受三个力,a受五个力 B、b受三个力,a受四个力 C、a与墙壁之间可能存在摩擦力 D、a、b之间不一定存在摩擦力
A、b受三个力,a受五个力 B、b受三个力,a受四个力 C、a与墙壁之间可能存在摩擦力 D、a、b之间不一定存在摩擦力 -
20、在空易拉罐中注入适量的水后,将易拉罐倾斜放置在水平桌面上,结果易拉罐“倾而不倒”,如图所示。下列说法正确的是( )
 A、注水后,易拉罐的重心位置升高了 B、易拉罐的重心位置在过易拉罐与桌面接触点的竖直线上 C、若将注水后的易拉罐水平放置,则其重心位置不变 D、若将空易拉罐压瘪,则其重心位置不变
A、注水后,易拉罐的重心位置升高了 B、易拉罐的重心位置在过易拉罐与桌面接触点的竖直线上 C、若将注水后的易拉罐水平放置,则其重心位置不变 D、若将空易拉罐压瘪,则其重心位置不变