相关试卷
- 广东省惠州市2017年高考物理一调试卷
- 广东省阳江市2016-2017学年高二下学期物理期末考试试卷
- 广东省佛山市高明一中2016-2017学年高一下学期物理期末模拟试卷
- 广东省珠海市2016-2017学年高二上学期物理期末考试试卷(b卷)
- 广东省惠州市2016-2017学年高二上学期物理期末考试试卷
- 浙江省嘉兴市2016-2017学年高三上学期物理期末考试试卷
- 辽宁省沈阳市2016-2017学年高三上学期物理期末考试试卷
- 江西省赣州市2016-2017学年高三上学期物理期末考试试卷
- 广东省清远市清城区2016-2017学年高三上学期物理期末考试试卷(b卷)
- 2016-2017学年广东省肇庆市高一上学期期末物理试卷
-
1、某物流公司安装一货物传送通道,货物从的平台无初速进入斜面通道,斜面通道末端与水平通道通过小圆弧连接,使货物经过此拐点时,速率能保持不变。斜面通道倾角为 , 斜面通道和货物之间的动摩擦因数 , 重力加速度取 , , 。
 (1)、求货物沿斜面通道下滑时的加速度大小;(2)、若水平通道长度只有 , 为保证货物不滑出,货物与水平通道之间的动摩擦因数至少多大?(3)、若水平通道足够长且制造材料与斜面通道相同,并可通过调节斜面通道的长度来改变 , 请写出全过程货物水平位移与之间可能的关系。
(1)、求货物沿斜面通道下滑时的加速度大小;(2)、若水平通道长度只有 , 为保证货物不滑出,货物与水平通道之间的动摩擦因数至少多大?(3)、若水平通道足够长且制造材料与斜面通道相同,并可通过调节斜面通道的长度来改变 , 请写出全过程货物水平位移与之间可能的关系。 -
2、如图所示,水平地面上有一小车,用两段不可伸长的轻绳将一质量为的小球悬挂在车厢水平顶部的A、B处,且。重力加速度为 , 求:
 (1)、小球和车都静止时,轻绳上张力的大小;(2)、当轻绳恰好伸直但没有张力时,小车运动的加速度;(3)、当小车以的加速度向右加速时,绳上张力大小。
(1)、小球和车都静止时,轻绳上张力的大小;(2)、当轻绳恰好伸直但没有张力时,小车运动的加速度;(3)、当小车以的加速度向右加速时,绳上张力大小。 -
3、如图所示,质量为的物块A放在静止的木箱内,A和木箱水平底面之间的动摩擦因数为。A被一根劲度系数为的轻弹簧向右拉着而保持静止,此时弹簧的伸长量为。设最大静摩擦力等于滑动摩擦力,取。求:
 (1)、A所受弹簧的弹力大小;(2)、要使A能相对木箱底面向左移动,木箱水平运动的加速度至少多大?
(1)、A所受弹簧的弹力大小;(2)、要使A能相对木箱底面向左移动,木箱水平运动的加速度至少多大? -
4、如图所示,足球场上沿直线等间距地摆放着7个定位锥筒,锥筒间距为。某同学在号锥筒位置将足球沿平行于锥筒摆放的连线方向踢出,足球向右匀减速运动,用时恰好停在号锥筒位置。求该足球:
 (1)、运动时的加速度大小;(2)、经过号和号锥筒中间位置点时的速率。
(1)、运动时的加速度大小;(2)、经过号和号锥筒中间位置点时的速率。 -
5、某小组探究“质量不变时,物体加速度与其所受合外力的关系”。实验装置如图1所示,让小车右端和纸带相连,左端用细绳跨过定滑轮和槽码相连。
 (1)、该实验我们采用的研究方案是________(只有一个选项正确);A、保持小车质量不变,改变槽码质量 B、保持槽码质量不变,改变小车质量 C、保持槽码和小车的总质量不变 D、同时改变槽码质量和小车质量(2)、该实验过程中操作正确的是________(只有一个选项正确);A、补偿阻力时小车需连接纸带 B、使小车质量远小于槽码质量 C、释放小车后立即打开打点计时器 D、调节滑轮高度使细绳与水平桌面平行(3)、实验中得到了一系列打点纸带,其中一条纸带的计数点如图2所示,相邻两点之间的距离分别为 , , …, , 时间间隔均为。
(1)、该实验我们采用的研究方案是________(只有一个选项正确);A、保持小车质量不变,改变槽码质量 B、保持槽码质量不变,改变小车质量 C、保持槽码和小车的总质量不变 D、同时改变槽码质量和小车质量(2)、该实验过程中操作正确的是________(只有一个选项正确);A、补偿阻力时小车需连接纸带 B、使小车质量远小于槽码质量 C、释放小车后立即打开打点计时器 D、调节滑轮高度使细绳与水平桌面平行(3)、实验中得到了一系列打点纸带,其中一条纸带的计数点如图2所示,相邻两点之间的距离分别为 , , …, , 时间间隔均为。①为减小 , , …,的测量误差,需要用刻度尺量出各计数点到第1个计数点的距离,某一计数点在刻度尺上位置如图3所示,其读数为cm;
②下列加速度算式中,最优的是;
A.
B.
C.
D.
(4)、两位同学用不同质量的小车分别进行了实验,并作出图4中的甲、乙图线,其中为小车加速度,为槽码所受重力。请根据图线判断两次实验小车的质量关系为(选填“>”、“=”或“<”),并结合所学知识说明理由。
-
6、如图所示,、两个物体相互接触(不黏合),放置在光滑水平面上,已知 , 。从开始,推力和拉力随时间的变化规律为: , 。则、之间的相互作用力、的加速度 , 的加速度随时间变化关系图像可能正确的是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
7、用三根细线、、将两个相同小球和连接,并如图悬挂。两小球处于静止状态,其中细线水平。将三根绳的张力大小分别记作、、 , 则它们的大小关系是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、时刻从某点竖直上抛一个小球,用一台固定的相机每隔时间拍一张照片(不计曝光时间),、、时刻的照片从左向右排列如图所示,不计空气阻力,重力加速度为 , 则小球的初速度为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9、如图甲所示,一个木棒受到三个拉力、、的作用,三个力的矢量恰好能围成一个正三角形,如图乙所示。则此三个力的合力是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、2024年9月11日,我国自主研发的朱雀三号火箭十公里级垂直起降飞行试验成功。在某次测试中,该型火箭竖直起降的速度-时间图像如图所示,则下列说法正确的是( )
 A、内,火箭加速度一直增大 B、时刻,火箭已到达最高位置 C、时刻,火箭已返回到起飞点 D、图中两处阴影区域面积相等
A、内,火箭加速度一直增大 B、时刻,火箭已到达最高位置 C、时刻,火箭已返回到起飞点 D、图中两处阴影区域面积相等 -
11、如图所示,一物体用细绳悬于点,现用另一细绳绑住绳上的点,对点施加水平牵引力,使物体缓慢上升,则此过程中,关于绳、绳拉力、大小的变化,下列判断正确的是( )
 A、变大、变大 B、变小、变大 C、变小、变小 D、变大、变小
A、变大、变大 B、变小、变大 C、变小、变小 D、变大、变小 -
12、在“探究两个互成角度的力的合成规律”的实验过程中,丁图中是以乙图中、为邻边在同一标度下所作平行四边形的对角线,则( )
 A、两弹簧测力计的拉力方向一定互成 B、两次拉橡皮筋时点位置一定要相同 C、两弹簧测力计的拉力读数一定要相等 D、丁图中与丙图中的大小一定相等
A、两弹簧测力计的拉力方向一定互成 B、两次拉橡皮筋时点位置一定要相同 C、两弹簧测力计的拉力读数一定要相等 D、丁图中与丙图中的大小一定相等 -
13、人站在商场扶梯的水平台阶上由1楼匀速前往2楼,人所受的重力为 , 则( )
 A、电梯对人的摩擦力方向水平向左 B、人所受合外力方向与运动方向相同 C、电梯对人的支持力与是一对平衡力 D、电梯对人的支持力与是一对相互作用力
A、电梯对人的摩擦力方向水平向左 B、人所受合外力方向与运动方向相同 C、电梯对人的支持力与是一对平衡力 D、电梯对人的支持力与是一对相互作用力 -
14、“朝辞白帝彩云间,千里江陵一日还;两岸猿声啼不住,轻舟已过万重山。”这句诗描绘了诗人从白帝城至江陵两地间乘船沿江而下的情景,从物理学的视角来看( )
 A、“一日”指的是“时刻” B、“千里”指的是“位移” C、由诗能求得“平均速度” D、相对于轻舟,山在运动
A、“一日”指的是“时刻” B、“千里”指的是“位移” C、由诗能求得“平均速度” D、相对于轻舟,山在运动 -
15、下列选项中,物理量全部是矢量的是( )A、路程 速度 B、位移 加速度 C、速率 重力 D、位移 时间
-
16、国庆放假期间,全国高速公路免费通行,小轿车可以不停车通过收费站,但要求小轿车通过收费站窗口中心线前=9m区间的速度不超过=6m/s。如图所示,现有甲、乙两小轿车在收费站前平直公路上分别以=20m/s和=34m/s的速度匀速行驶,甲车在前,乙车在后。甲车司机发现正前方收费站立即刹车,做加速度大小为=2m/s2的匀减速直线运动,到达收费站窗口前9m处速度恰好减为6m/s,并以该速度匀速通过收费站窗口前区间。求:
 (1)、甲车司机刹车时离收费站窗口中心线的距离;(2)、若甲车通过收费站窗口中心线后立即做加速度大小为a=5m/s2的匀加速直线运动,直至=25m/s后匀速行驶,求甲车从开始减速至运动到速度为所用时间;(3)、若乙车司机在发现甲车刹车时经=0.5s的反应时间后开始刹车,乙车做加速度大小为=4m/s2的匀减速直线运动。为避免两车相撞,且乙车在收费站窗口前9m区不超速,则在甲车司机开始刹车时,甲、乙两车至少相距多远?
(1)、甲车司机刹车时离收费站窗口中心线的距离;(2)、若甲车通过收费站窗口中心线后立即做加速度大小为a=5m/s2的匀加速直线运动,直至=25m/s后匀速行驶,求甲车从开始减速至运动到速度为所用时间;(3)、若乙车司机在发现甲车刹车时经=0.5s的反应时间后开始刹车,乙车做加速度大小为=4m/s2的匀减速直线运动。为避免两车相撞,且乙车在收费站窗口前9m区不超速,则在甲车司机开始刹车时,甲、乙两车至少相距多远? -
17、高空抛物被形象地称作“悬在城市上空的痛”。为制止这种不文明的行为,某小区物业在每栋楼前架设了一台高清摄像机。在一次高空抛物事件中,查看该摄像机拍摄的一段录像时发现,如图所示,某物体经过三楼所用的时间为t=0.2s。已知物体在空中做自由落体运动,且每层楼的高度为h=3.2m,重力加速度大小为g。求:
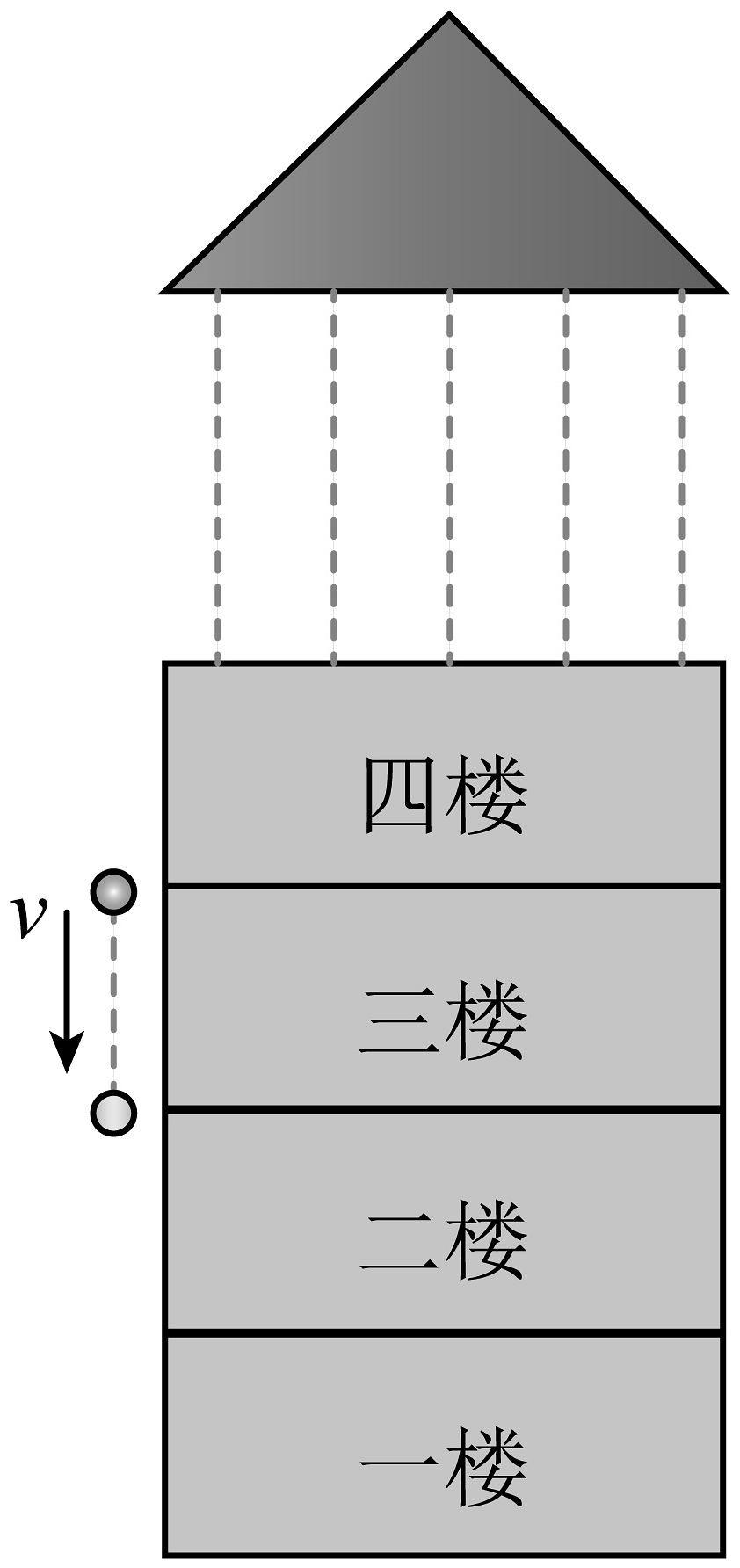 (1)、物体刚到达三楼住户楼顶时的速度大小v;(2)、通过计算判断物体是哪层楼的住户抛下的。
(1)、物体刚到达三楼住户楼顶时的速度大小v;(2)、通过计算判断物体是哪层楼的住户抛下的。 -
18、质量为4kg的物体,放在水平的地板上,用一轻质弹簧水平拉该物体,当弹簧的伸长量为2.5cm时,物体恰好能够从静止开始运动:当弹簧拉着该物体匀速前进时,弹簧伸长量为2cm,已知弹簧的劲度系数为(g取),求:
(1)物体受到的最大静摩擦力为多大?
(2)物体与地板之间的滑动摩擦因数为多少?
-
19、在一段直线公路上,甲、乙两车在同一车道上同向行驶,甲车在前,乙车在后,速度均为18m/s,相距35m。在t=0时刻,甲车司机发现前方十字路口处有一辆货车突然冲出来,于是马上采取措施,如图中的甲、乙两图分别是甲、乙两车的运动图像,取初速度方向为正方向,则下列说法正确的是( )
 A、在2~5s内,甲车做匀变速直线运动 B、在0~5s内,乙车的平均速度为13.5m/s C、甲、乙两车在3.5s末速度相等 D、在0~5s内,甲、乙两车的最小距离为3.5m
A、在2~5s内,甲车做匀变速直线运动 B、在0~5s内,乙车的平均速度为13.5m/s C、甲、乙两车在3.5s末速度相等 D、在0~5s内,甲、乙两车的最小距离为3.5m -
20、一物体做匀变速直线运动,某时刻的速度大小为5m/s,经过1s后的速度大小变为13m/s,某同学对该物体在这1s内的运动进行分析,则下列分析正确的是( )A、物体速度变化量大小可能是18m/s B、位移的大小可能大于13m C、加速度的大小可能大于13m/s2 D、加速度的大小可能小于5m/s2