相关试卷
-
1、如图所示,匀速直线上升的热气球(可视为质点)突然受到方向水平向左、大小恒定的风力F,则( )
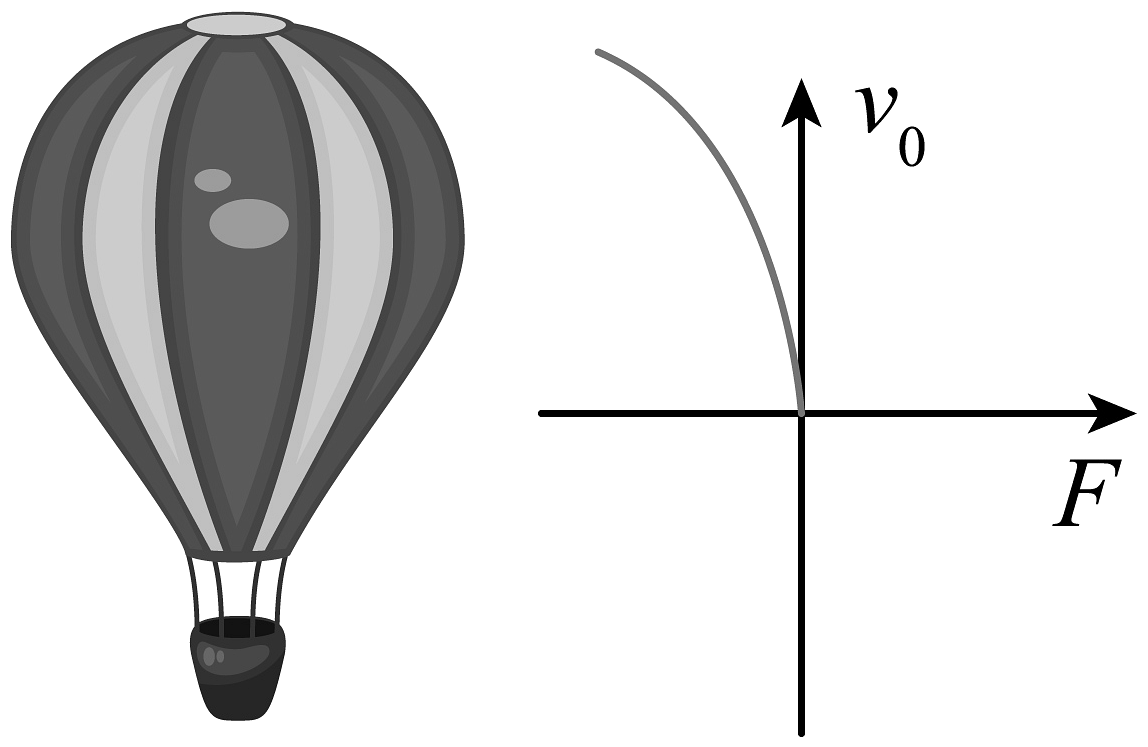 A、热气球将做曲线运动 B、热气球在相同时间内的速度变化量将越来越大 C、热气球将在竖直方向做减速运动 D、热气球的速度将先增大后减小
A、热气球将做曲线运动 B、热气球在相同时间内的速度变化量将越来越大 C、热气球将在竖直方向做减速运动 D、热气球的速度将先增大后减小 -
2、如图所示,长为L的轻杆一端用光滑铰链固定,另一端固定一质量为m小球A,将小球放置在倾角为60°,质量也为m的斜面体B上,不计一切摩擦。在斜面体的右侧加水平向左的推力,斜面和轻杆保持静止,轻杆与水平方向的夹角为30°,重力加速度为g。
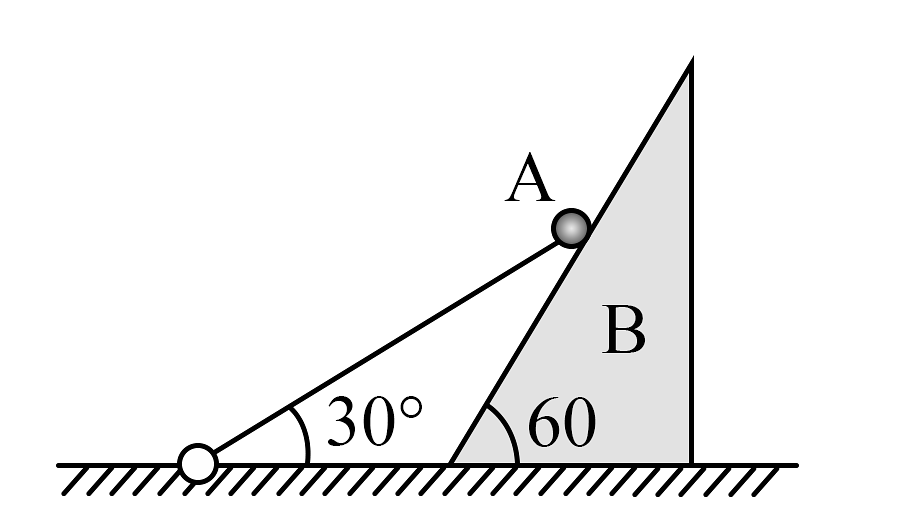 (1)、求斜面对小球的支持力大小FN;(2)、若撤去外力,求撤去外力瞬间小球的加速度大小a;(3)、若撤去外力时小球与轻杆脱离,小球从静止开始下滑,求小球刚要滑到地面时,斜面体的速度大小v。
(1)、求斜面对小球的支持力大小FN;(2)、若撤去外力,求撤去外力瞬间小球的加速度大小a;(3)、若撤去外力时小球与轻杆脱离,小球从静止开始下滑,求小球刚要滑到地面时,斜面体的速度大小v。 -
3、静电除尘装置的简化原理图,如图所示。长为L的两块平行带电极板间为除尘空间。质量为m、电荷量为-q的带电尘埃分布均匀,均以沿板方向的速率v射入除尘空间,当其碰到下极板时尘埃被收集。现给两极板间加U0的电压,进入的尘埃恰好都能被收集。不计重力及尘埃间的相互作用。
 (1)、求尘埃在极板内运动的最长时间t和最大动能Ek;(2)、求从平行板中心射入的尘埃被收集时,距离入口的水平距离x;(3)、当板间电压调为0.8U0时,求能够被收集的尘埃量与总尘埃量的比值k。
(1)、求尘埃在极板内运动的最长时间t和最大动能Ek;(2)、求从平行板中心射入的尘埃被收集时,距离入口的水平距离x;(3)、当板间电压调为0.8U0时,求能够被收集的尘埃量与总尘埃量的比值k。 -
4、“卫星巡田”让农业生产焕发新活力。卫星绕两极在距地面h高度的圆轨道上运行,监测的农田南北长为l,地球的半径为R,地球表面重力加速度为g,忽略地球自转。求:(1)、该卫星的运行速度大小v;(2)、该卫星通过农田正上方的时间t。
-
5、某波源S发出一列简谐横波,波源S的振动图像如图所示。在波的传播方向上有A、B两点,它们到S的距离分别为45m和55m。A、B两点开始振动的时间间隔为0.5s。求:
 (1)、这列波的波长λ;(2)、当B点处于平衡位置时,A点离开平衡位置的位移是多少?
(1)、这列波的波长λ;(2)、当B点处于平衡位置时,A点离开平衡位置的位移是多少? -
6、某同学要将小量程的直流电压表表头VA改装成量程为3V的电压表。表头VA内阻未知,该同学先测量表头VA的内阻,然后将表头进行改装。可使用的器材如下:电源,滑动变阻器,定值电阻(阻值为R0),标准电压表VB。具体实验步骤如下:

甲方案:
①按图a连接电路;
②闭合开关S1、S2 , 移动滑片P至某位置,读出VA的示数为U1;
③保持滑片P位置不变,断开S2 , 读出VA的示数为U2;
④求出电压表表头VA的内阻r。
乙方案:
①按图b连接电路;
②闭合开关S1 , 逐步移动滑片P,记录多组VA和VB的示数;
③根据VA和VB的示数作出UB-UA图像(如图c所示);
④求出电压表表头VA的内阻r'。
(1)、甲、乙方案的步骤②中,闭合开关S1前滑片P应调至端。(选填“左”或“右”)(2)、甲方案中,由示数U1、U2和电阻R0 , 可求得r=。(3)、乙方案中,UB-UA的图像是一条过原点的倾斜直线,直线的斜率为k。由此可求得电压表表头VA的内阻r'=。(4)、比较甲、乙两方案,可知rr'。(选填“<”、“>”或“=”)(5)、将小表头改装后,与标准电压表并联,测量某电路两端的电压。改装表读数2.40V,而标准电表读数2.50V,此时改装表的相对误差为%。(结果保留两位有效数字) -
7、如图所示,物体与压缩的弹簧连接,物体静止放上水平顺时针转动的传送带上,皮带的速度为v0 , 传送带足够长且表面粗糙,则物体运动的v-t图像可能的是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
8、如图所示,一T型支架长的横杆上用等长的细线等间距悬挂4个相同小球A、B、C、D,支架绕轴线缓慢加速转动,当支架转动的角速度为ω时( )
 A、A、D的加速度相同 B、A、B的悬线与竖直方向的夹角相等 C、A的机械能大于B的机械能 D、A的动能等于该过程中细线对A做的功
A、A、D的加速度相同 B、A、B的悬线与竖直方向的夹角相等 C、A的机械能大于B的机械能 D、A的动能等于该过程中细线对A做的功 -
9、如图所示,一负点电荷固定在O点,下方有一块无穷大的接地金属板,a、b、c、d四点到O点距离相等,且ac垂直于bd,各点的场强大小E、电势φ关系正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、电动机M的内阻和电阻R的阻值相等,将它们并联接入电路,闭合开关,电动机正常工作。则电路中的电流I、消耗的电功率P关系表达正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、汽车定速巡航行驶(速度大小不变),通过如图所示的路段,1、2上坡,3、4下坡,路面对汽车的摩擦阻力和空气阻力大小恒定,汽车经过1、2、3、4位置时发动机的功率( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、如图所示,两固定的正点电荷+Q相距2L,连线的中点有负点电荷-Q。将负电荷移至无穷远处,外力至少需要做功( )
 A、零 B、 C、 D、
A、零 B、 C、 D、 -
13、列车静止时,静止的观察者听到列车上发出频率一定的声音。下列情况中,观察者会听到这个声音的音调变高的是( )A、观察者静止,列车远离观察者行驶 B、列车静止,观察者乘汽车向着列车运动 C、观察者乘坐该列车,列车在向前加速运动 D、观察者乘坐该列车,列车在向前减速运动
-
14、如图所示,在铁架台的横梁上固定两个单摆,把它们拉起一小角度后释放,研究单摆的振动周期,则( )
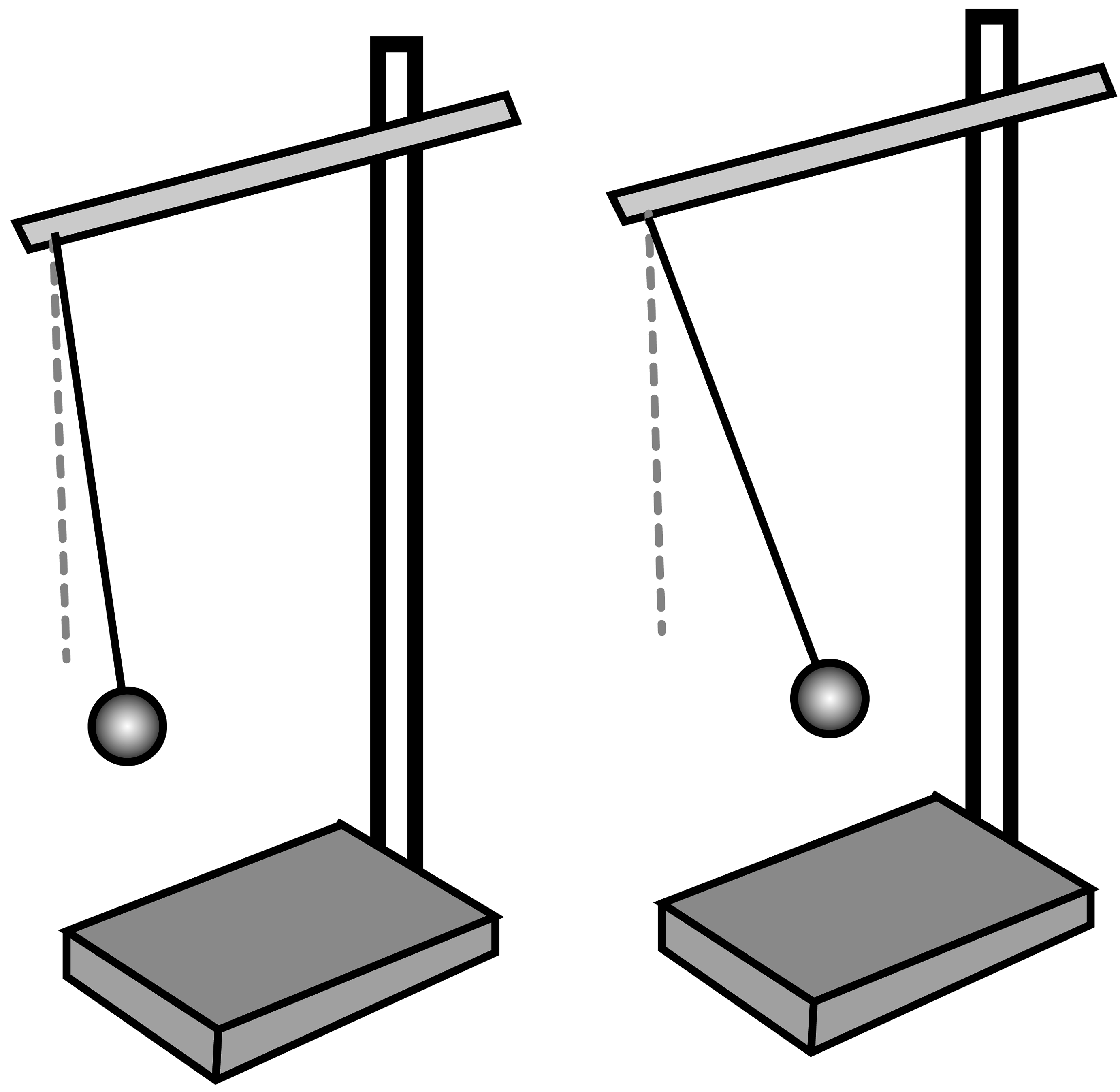 A、摆线越短周期越小 B、摆角越小周期越小 C、摆球越重周期越小 D、横梁越低周期越小
A、摆线越短周期越小 B、摆角越小周期越小 C、摆球越重周期越小 D、横梁越低周期越小 -
15、利用电容器可监测水位的变化。如图所示,两块平行金属板表面已进行绝缘处理,当水位升高时( )
 A、电容变小,极板上电荷量减少 B、电容变小,极板上电荷量增加 C、电容变大,极板上电荷量减少 D、电容变大,极板上电荷量增加
A、电容变小,极板上电荷量减少 B、电容变小,极板上电荷量增加 C、电容变大,极板上电荷量减少 D、电容变大,极板上电荷量增加 -
16、如图所示,在光滑的水平面上放着一个质量为的木箱,拉力与水平方向成60°角,。木箱从静止开始运动,内拉力做的功为J。

-
17、质点做直线运动的图像如图所示,则质点在内的位移为。
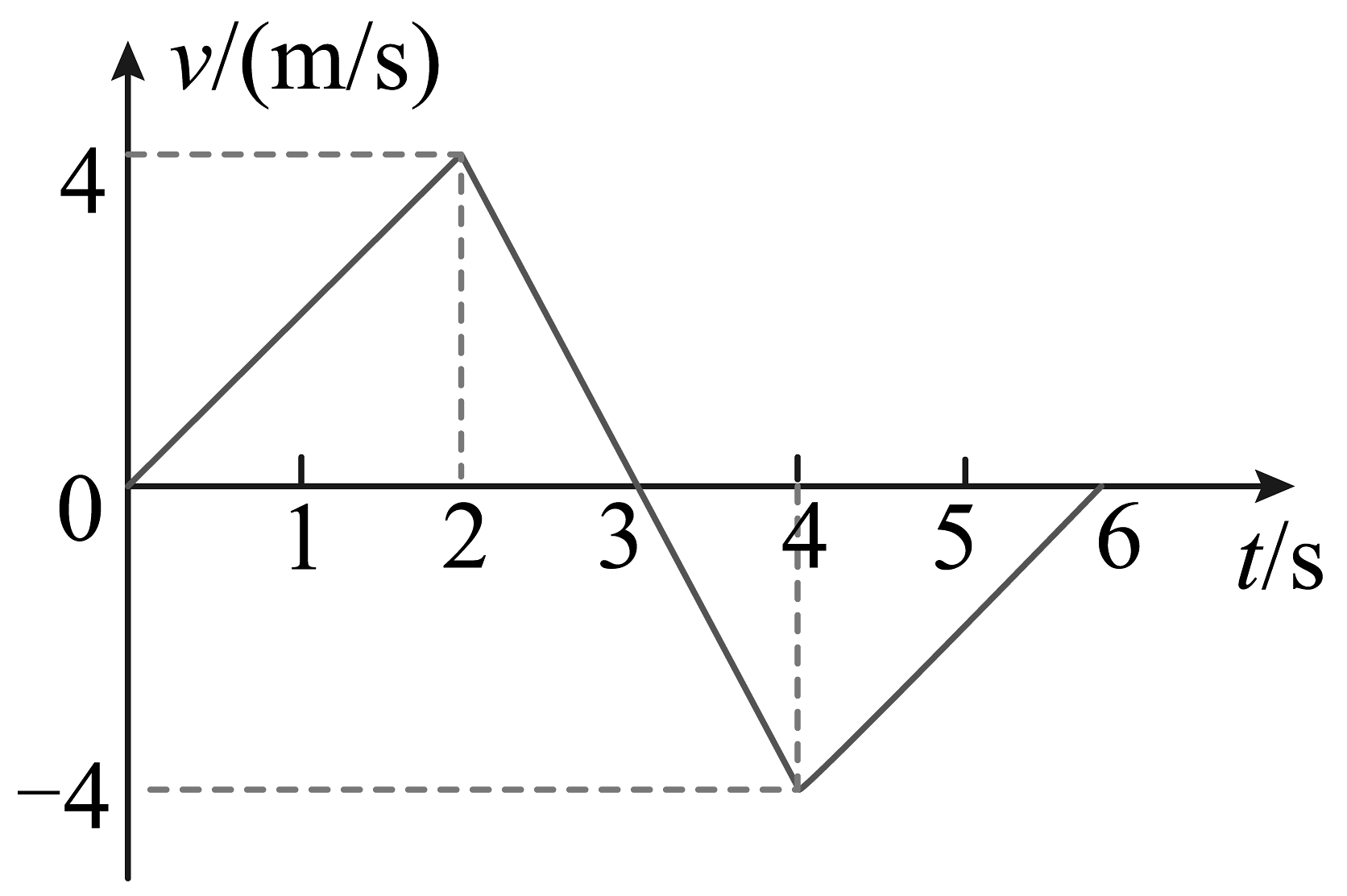
-
18、如图为一正在测量中的多用电表的表盘。
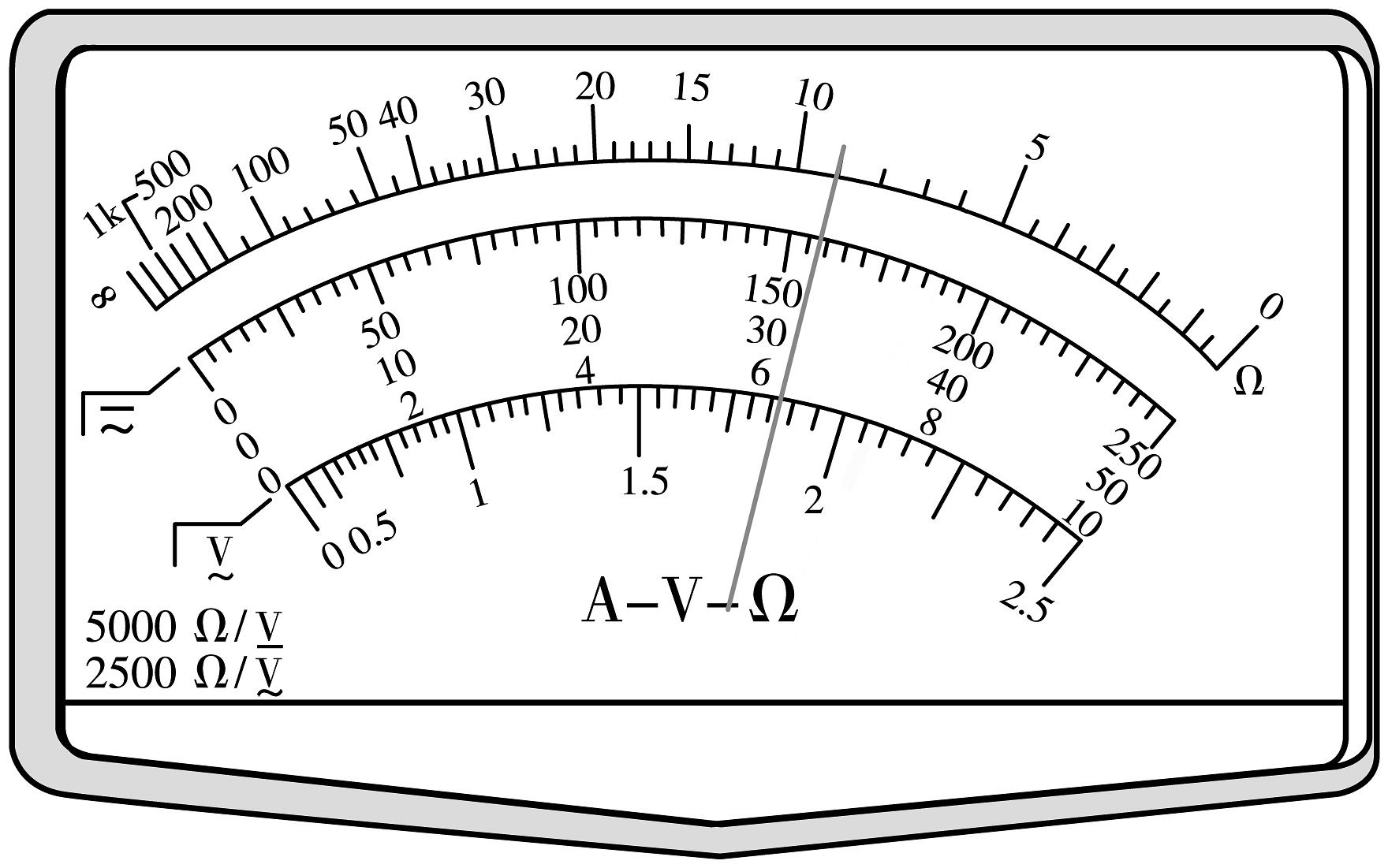
如果用×100挡测电阻,则多用电表的读数为Ω。
-
19、检验电荷在电场中受到的电场力为 , 测得该点的场强为;若将检验电荷的电量减小一半,放回原处,则该点的电场强度为。
-
20、韩晓鹏是我国首位在冬奥会雪上项目夺冠的运动员。他在一次自由式滑雪空中技巧比赛中沿“助滑区”保持同一姿态下滑了一段距离,重力对他做功 , 他克服阻力做功。韩晓鹏在此过程中动能增加了J。